Прискорення точки при координатному способі задання її руху

Нехай рух точки задано в декартовій системі координат:

; ; .

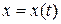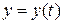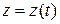Визначимо вектор швидкості точки у вигляді :

,

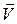
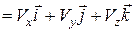де 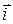, , 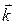– орти відповідно координатних осей , , .

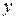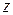Тоді, вектор прискорення дорівнює:

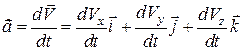. (12.16)

Проектуючи векторну рівність (12 .16) на осі , , 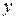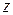і враховуючи формули (12.6), одержимо формули для проекцій вектора прискорення на координатні осі:

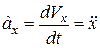
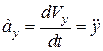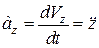; . (12.17)

Отже, проекції вектора прискорення точки на нерухомі координатні осі дорівнюють першим похідним за часом від відповідних проекцій швидкості або другим похідним за часом від відповідних координат точки.

Знаючи проекції прискорення на координатні осі, його модуль і напрям знаходимо за наступними формулами:

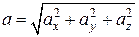, (12.18)

; ; .

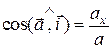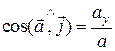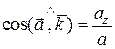Одиниці вимірювання прискорення точки – см/сек² або м/сек².