Швидкість точки при натуральному способі задання її руху

Нехай рух точки задано натуральним способом, тобто відомі траєкторія, початок і додатний напрям дугової координати 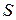 , а також рівняння руху точки за цією траєкторією
, а також рівняння руху точки за цією траєкторією 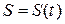 (рис. 12.2).
(рис. 12.2).
Із довільної точки О проведемо радіус-вектор 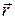 точки М.
точки М.
Будемо розглядати цей вектор як складну функцію часу
 . (12.8)
. (12.8)
На підставі (12.2), враховуючи (12.8), одержимо вектор швидкості точки 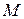 у такому вигляді:
у такому вигляді:
 . (12.9)
. (12.9)
Розглянемо перший співмножник виразу (12.9) у такій формі:
 .
.
Як витікає з рис. 12.2, модуль цього вектора, як границя відношення довжини нескінченно малої хорди  до довжини стягнутої нею дуги
до довжини стягнутої нею дуги 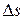 , дорівнює:
, дорівнює:
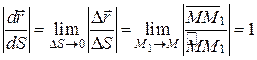 . (12.10)
. (12.10)
Напрям одиничного за величиною вектора (12.10) завжди збігається з напрямом дотичної в бік збільшення дугової координати, тобто
 , (12.11)
, (12.11)
де 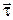 – орт дотичної до траєкторії.
– орт дотичної до траєкторії.
З урахуванням (12.11) вираз (12.9) набуває вигляду:
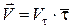 , (12.12)
, (12.12)
де
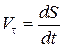 . (12.13)
. (12.13)
Із (12.13) видно, що  може бути більше або менше від нуля в залежності від того, збільшується або зменшується дугова координата рухомої точки.
може бути більше або менше від нуля в залежності від того, збільшується або зменшується дугова координата рухомої точки.
Тому  , що дорівнює першій похідній за часом від дугової координати, являє собою проекцію вектора швидкості на дотичну, тобто визначає алгебраїчну величину швидкості.
, що дорівнює першій похідній за часом від дугової координати, являє собою проекцію вектора швидкості на дотичну, тобто визначає алгебраїчну величину швидкості.
Отже, вектор швидкості при натуральному способі задання руху точки дорівнює добутку проекції швидкості на дотичну до траєкторії  і орта дотичної
і орта дотичної 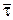 .
.
Дата добавления: 2014-12-20; просмотров: 3135;
