Прискорення точки при векторному способі задання її руху

В загальному випадку криволінійного руху точки її швидкість змінюється за величиною і напрямом. Ця зміна характеризується прискоренням точки.

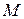Нехай у момент часу точка мала положення і її швидкість дорівнювала 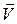, а у момент часу знаходилася у положенні і її швидкість дорівнювала . Приріст вектора швидкості точки за проміжок часу 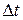дорівнює 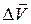(рис. 12.3, а).

Відношення 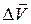до проміжку часу 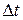називають середнім прискоренням точки за цей проміжок часу:

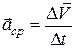. (12.14)

Прискорення точки у даний момент часу одержимо як границю середнього прискорення, коли проміжок часу 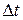наближається до нуля:

.

. (12.15)

Отже, вектор прискорення точки дорівнює першій похідній від вектора швидкості точки або другій похідній від радіуса-вектора точки за часом.

Щоб встановити напрям вектора прискорення точки, введемо поняття годографа швидкості.

З рис. 12.3, б бачимо, що швидкість точки N, яка описує годограф швидкості маючи радіус-вектор , дорівнює прискоренню точки М при її русі по траєкторії:

,

тобто .

Отже, вектор прискорення 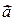точки М направлений паралельно дотичній до годографа вектора швидкості у відповідній точці в бік угнутості траєкторії точки.