Приклади розв’язання задач
Приклад 1. Рух точки задано рівняннями:
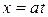 ;
; 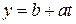 .
.
Визначити рівняння траєкторії точки.
 Розв’язання. 3 першого рівняння знайдемо час t і, підставляючи його значення у друге, одержимо рівняння траєкторії точки в координатній формі:
Розв’язання. 3 першого рівняння знайдемо час t і, підставляючи його значення у друге, одержимо рівняння траєкторії точки в координатній формі:
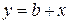 .
.
Це рівняння прямої, але траєкторією буде не вся пряма, а тільки та її частина, по якій рухається точка. З рівнянь руху витікає, що на початку руху (  ) точка
) точка 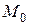 мала координати
мала координати  =0,
=0, 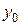 =b. Із збільшенням часу координати точки збільшуються.
=b. Із збільшенням часу координати точки збільшуються.
Отже, траєкторією точки буде та частина прямої, яка на рис. 11.4 показана суцільною лінією.
Приклад 2. Рух точки задано у декартових координатах рівняннями:
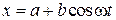 ;
;  ,
,
де  ,
, 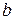 і
і  – сталі. Перейти до натурального способу задання руху точки.
– сталі. Перейти до натурального способу задання руху точки.
Розв’язання. Із заданих рівнянь вилучимо час  . Для цього у першому рівнянні величину
. Для цього у першому рівнянні величину  переносимо в ліву частину. Далі, підносимо обидва рівняння у другий ступінь і додавши їх, отримаємо рівняння траєкторії точки у координатній формі:
переносимо в ліву частину. Далі, підносимо обидва рівняння у другий ступінь і додавши їх, отримаємо рівняння траєкторії точки у координатній формі:  .
.
 Траєкторія точки – коло радіуса
Траєкторія точки – коло радіуса 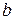 , центр якого має координати
, центр якого має координати  (рис. 11.5).
(рис. 11.5).
При  координати точки
координати точки 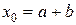 ,
,  , тобто точка знаходилась в положенні
, тобто точка знаходилась в положенні 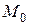 . З рівнянь руху виходить, що за зростанням
. З рівнянь руху виходить, що за зростанням  координата
координата  зменшується, а координата
зменшується, а координата 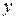 збільшується. Отже, точка з початкового положення
збільшується. Отже, точка з початкового положення 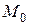 рухається у напрямку, що показано стрілкою на рис. 11.5.
рухається у напрямку, що показано стрілкою на рис. 11.5.
Обчислюємо похідні від заданих рівнянь:
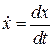
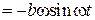 ;
; 
 .
.
За формулою (11.6) одержимо рівняння руху точки за траєкторією:
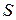 =
=  .
.
Отже, точка описує коло радіуса b з центром С так, що її дугова координата 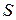 збільшується пропорційно часу за лінійним законом.
збільшується пропорційно часу за лінійним законом.
Приклад 3. За заданими рівняннями руху точки
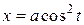 ;
; 
знайти рівняння її траєкторії, визначити цю траєкторію, а також знайти закон руху точки за траєкторією, відраховуючи відстань від початкового положення точки.
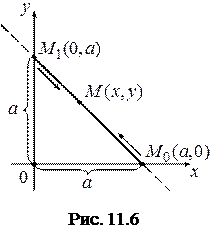 Розв’язання. Рівняння траєкторії точки у координатній формі – рівняння прямої
Розв’язання. Рівняння траєкторії точки у координатній формі – рівняння прямої
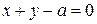 .
.
Траєкторія точки – це відрізок прямої, позначений на рис. 11.6 суцільною лінією. Рух точки починається з положення  . Через час
. Через час  точка займе положення
точка займе положення  , а через
, а через 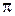 повернеться у точку
повернеться у точку  .
.
Враховуючи формулу (11.6) знаходимо рівняння руху за траєкторією:
 ,
,  ;
;


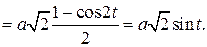
Отже, точка рухається вздовж відрізка  в його межах за гармонійним законом, тобто відстань
в його межах за гармонійним законом, тобто відстань  М відповідно збільшується або зменшується.
М відповідно збільшується або зменшується.
Приклад 4. Рух точки, що описує фігуру Ліссажу, задається рівняннями:
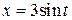 ;
;  .
.
Знайти рівняння траєкторії точки, побудувати цю траєкторію та визначити напрям руху точки у різні моменти часу. Знайти також найближчий після початку руху момент часу  , коли траєкторія перетинає вісь Ох.
, коли траєкторія перетинає вісь Ох.
Розв’язання.Враховуючи обмеження з рівнянь руху точки  ;
;  , встановлюємо область розташування траєкторії точки (рис. 11.7).
, встановлюємо область розташування траєкторії точки (рис. 11.7).
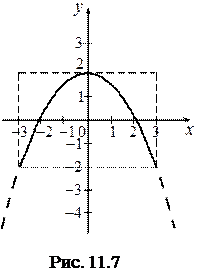 Знайдемо рівняння траєкторії у координатній формі, вилучивши з рівнянь руху параметр
Знайдемо рівняння траєкторії у координатній формі, вилучивши з рівнянь руху параметр  . Для цього з першого рівняння виділимо:
. Для цього з першого рівняння виділимо:

і піднесемо до квадрату:
 .
.
Використовуючи формулу з тригонометрії
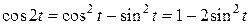 ,
,
запишемо:
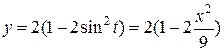 .
.
Звідки отримуємо:
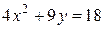 .
.
Це рівняння квадратної параболи з вертикальною віссю симетрії 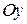 .Траєкторієюточки є верхівка цієї параболи, що знаходиться у середині визначеної областіі показана на рис. 11.7 суцільною лінією.
.Траєкторієюточки є верхівка цієї параболи, що знаходиться у середині визначеної областіі показана на рис. 11.7 суцільною лінією.
Момент часу  – момент перетину точкою
– момент перетину точкою 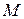 осі
осі 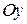 після початку руху відповідає координаті
після початку руху відповідає координаті
 .
.
Враховуючи, що  , маємо:
, маємо:
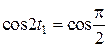 ;
;  ,
,
тобто
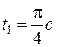 .
.
Дата добавления: 2014-12-20; просмотров: 7092;
