Координатний спосіб задання руху точки

Положення рухомої точки відносно обраної системи відліку визначається її координатами. Якщо обрано декартову систему координат 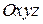, то для вивчення руху точки повинні бути задані координати цієї точки (рис. 11.2) як функції часу – :

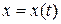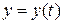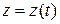; ; . (11.2)

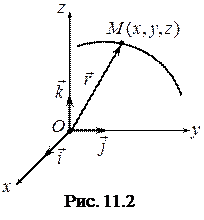Функції (11.2) називаються рівняннями руху точки в координатній формі.

Ці рівняння визначають закон руху точки, бо дозволяють для кожного моменту часу вказати положення точки у просторі.

Якщо точка рухається в одній площині наприклад, 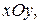то рівняння руху матимуть вигляд:

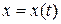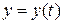; . (11.3)

Водночас (11.2) і (11.3) являють собою рівняння траєкторії точки в параметричній формі.

Щоб отримати рівняння траєкторії точки в координатній формі, треба з рівнянь (11.2) чи (11.3) вилучити певним чином параметр .

Між координатним і векторним способами існує зв’язок.. Оскільки проекції радіуса-вектора 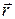точки М (рис. 11.2) на координатні осі дорівнюють координатам точки М, то

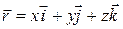, (11.4)

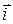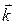де x, y, z – координати точки М, а , і – орти координатних осей.

Рівність (11.4) дозволяє перейти від координатного способу визначення руху точки до векторного.