Векторний спосіб задання руху точки

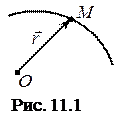Положення рухомої точки М можна визначити її радіусом-вектором 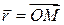, що проведений з нерухомої точки О (рис. 11.1). Під час руху точки її радіус-вектор змінюється з часом за модулем і за напрямком. Отже, він є певною векторною функцією від скалярного аргумента – часу :

. (11.1)

Рівняння (10.1) називається рівнянням руху точки у векторній формі і являє собою закон руху даної точки.

Введемо поняття годографа вектора. Годографом будь-якого вектора називається лінія, яку описує кінець цього вектора, що змінюється у часі, якщо його початок знаходиться в нерухомій точці.

Годограф радіуса-вектора 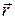точки М є траєкторією цієї точки.

Потрібно зауважити, що векторний спосіб зручний при теоретичних викладках своєю наочністю і компактністю запису. Він також є базовим при визначенні кінематичних характеристик іншими способами. Але векторний спосіб непридатний для практичних розрахунків, і тому кожного разу необхідно переходити до координатного чи натурального способів задання руху.