Приклад розв’язання задачі. Приклад. Рух точки М над горизонтальною поверхнею, задано рівняннями:
Приклад. Рух точки М над горизонтальною поверхнею, задано рівняннями:
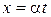 ;
; 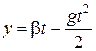 ,
,
де 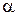 ,
, 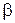 і
і 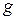 – сталі величини сталі. Визначити дотичне і нормальне прискорення точки, а також закон зміни радіуса кривини її траєкторії.
– сталі величини сталі. Визначити дотичне і нормальне прискорення точки, а також закон зміни радіуса кривини її траєкторії.
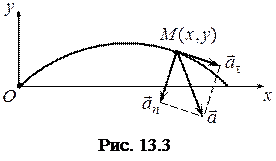 Розв’язання. Вилучивши час t із заданих рівнянь руху, одержимо рівняння траєкторії точки у координатній формі:
Розв’язання. Вилучивши час t із заданих рівнянь руху, одержимо рівняння траєкторії точки у координатній формі:
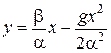 .
.
Це рівняння параболи. Частина цієї параболи, що знаходиться над горизонтальною поверхнею, є траєкторією точки (рис. 13.3).
Визначимо закони зміни швидкості і прискорення точки:
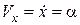 ;
;  ;
; 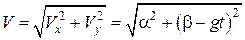 ;
;
 ;
;  ;
; 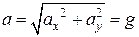 .
.
Знаходимо дотичне прискорення точки:
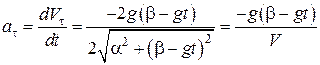 .
.
Для нормального прискорення точки маємо:
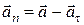
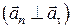 ;
; 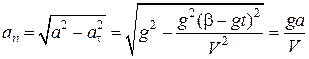 ;
; 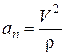 .
.
Підставляючи значення 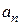 і V в останнюформулу, знайдемо закон зміни радіуса кривини траєкторії точки: за часом:
і V в останнюформулу, знайдемо закон зміни радіуса кривини траєкторії точки: за часом:
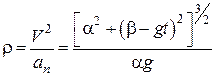 .
.
Якщо врахувати із рівнянь руху точки, що 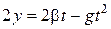 , і підставити цей вираз у чисельник останньої формули, то отримаємо закон зміни радіуса кривини відповідно до зміни ординати
, і підставити цей вираз у чисельник останньої формули, то отримаємо закон зміни радіуса кривини відповідно до зміни ординати 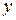 точки
точки 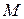 :
:
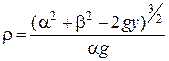 .
.
Дата добавления: 2014-12-20; просмотров: 1029;
