Метод непосредственной оценки
Он состоит в том, что диапазон изменения какой-либо качественной переменной разбивается на несколько интервалов, каждому из которых присваивается определенная оценка (балл), например от 0 до 10 (0-1, 0-100).
Задача эксперта поместить каждый из рассматриваемых объектов (факторов, альтернатив) в определенный оценочный интервал в соответствии со степенью обладания тем или иным свойством, либо в соответствии с представлением эксперта об их значимости.
Простейший случай непосредственной оценки - ответы "да", "нет", которые эксперт дает на вопросы анкеты. Может быть трехступенчатая - очень важно, важно, не важно (не имеет значения). Эти качественные суждения эксперта оцениваются по шкале с помощью цифр (баллов). Например, "да"-1, "нет"-0. Если трехступенчатая, то 2,1,0. От 1 до 10: чрезвычайно большой вклад - 10, большой вклад и т.д.
Размер шкалы должен быть таким, чтобы каждому баллу соответствовало определенное понятие, выражающее степень интенсивности свойства, качества или предпочтительности.
Использование рангов и непосредственных оценок (баллов) при составлении плановых альтернатив значительно упрощает выбор наиболее предпочтительной из них, поскольку позволяет соизмерить качественно различные факторы.
Однако имеется недостаток: относительно низкое качество одного из факторов можно компенсировать за счет более высокого качества другого фактора, получая один и тот же результат при различной фактической их значимости. Для повышения надежности таких оценок нужно выявить и установить количественно связи между всеми значимыми для выбора решения факторами.
С этой целью используются интервальные и порядковые шкалы, а также специальные методы: последовательных предпочтений, парных сравнений, последовательных интервалов и др. описание которых можно найти в специальной литературе.
Применение различных шкал и методов для измерения информации, получаемой от экспертов, основано на некоторых формальных правилах, которые обеспечивают непротиворечивость системы оценок, приписываемых экспертами различным событиям или факторам. Поскольку экспертные оценки в значительной степени являются вероятностными, для формирования системы оценок (весов) можно использовать некоторые теоремы теории вероятностей.
Мы просто сформулируем три основных правила приписания экспертных оценок событиям (факторам, альтернативам).
1. Сумма оценок, приписанных какому-либо ряду взаимоисключаемых событий должна быть равна 1.
2. Оценка, приписанная любому событию, должна быть числом в интервале между 0 и 1.
3. Если два или более взаимоисключающих события группируются в одно, то оценка, приписанная этому событию, должна быть равна сумме оценок, приписанных исходным событиям.
На практике в целях удобства расчетов сумма оценок для ряда событий может быть принята равной не только единице, но и другому фиксированному числу. В таких случаях для соблюдения основных правил приписания оценок можно произвести их нормирование. Для этого все оценки суммируются, а затем каждая из них делится на полученную сумму.
Покажем, как осуществляется нормирование оценок на примере. Представим, что при сравнении некоторых целей Ц1, Ц2, Ц3, Ц4 эксперт оценил их значимость следующим образом:
W1=9; W2=8; W3=4; W4=3.
Сумма оценок (весов) будет равна:
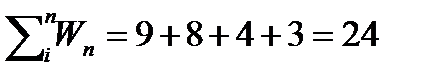
Произведем нормирование оценок, т.е. рассчитаем для каждой из них отношение по формуле :
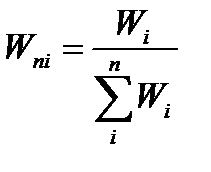
тогда W41 = 9/24; W42 = 8/24; W43 = 4/24; W44 = 3/24.
Ясно, что сумма нормированных оценок всегда равна единице, а каждая из них это число в интервале от нуля до единицы, нормирование обеспечивает соблюдение первого и второго правил приписывания оценок событиям. Кроме того, при помощи нормирования устанавливается зависимость между отдельными оценками взаимосвязанных объектов и их суммой.
Другой способ установления зависимости между оценками факторов состоит в том, что важнейшему (с точки зрения экспертов) фактору назначается оценка (вес), равная наперед заданному числу (обычно от 1 до 10), а оценка следующих друг за другом по важности факторов определяется последовательно, как доля более важного. Полученные таким образом значения нормируются. Основное достоинство такого способа установления взаимосвязанных оценок заключается в том, что он облегчает процесс их выбора. Поскольку эксперту не нужно каждый раз сопоставлять весь ряд оценок, а лишь учитывать значение первой и предыдущей по важности оценок.
Оценки, полученные от группы экспертов могут быть усреднены для каждого фактора путем расчета средней арифметической. В случаях, когда группа, состоящая из нескольких экспертов, оценивает ряд факторов, причем у каждого из них имеется своя шкала предпочтений для нахождения средней оценки каждого фактора может быть рекомендована следующая методика
1. Составляется матрица "эксперты-факторы", в которой проставляются полученные от каждого эксперта оценки факторов по шкале от 0 до 10. Представим, что два эксперта оценили шесть факторов так, как это показано в табл.
Таблица Оценка экспертами факторов
| Эксперты | ФАКТОРЫ | |||||
| Ф1 | Ф2 | Ф3 | Ф4 | Ф5 | Ф6 | |
| Э1 | ||||||
| Э2 |
2. Рассчитывается относительная значимость (WIJ) всех факторов в отдельности для каждого эксперта. С этой целью оценки, полученные от каждого эксперта, суммируются по (горизонтали), а затем нормируются.
W11 = 10/38; W21 = 7/38; W31 = 9/38; W41 = 3/38;
W51 = 4/38; W61 = 5/38;
W12 = 8/37; W22 = 6/37; W32 = 10/37; W42 = 3/37;
W52 = 4/37; W62 = 5/37.
3. Вычисляется усредненная оценка всеми экспертами каждого фактора. Для этого нормированные оценки, полученные в предыдущем шаге суммируются (во вертикали), а затем рассчитывается средняя арифметическая для каждого фактора.
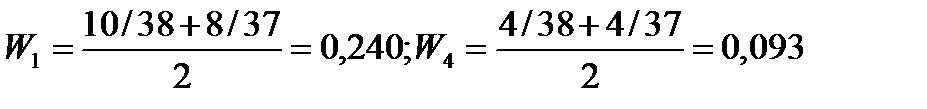
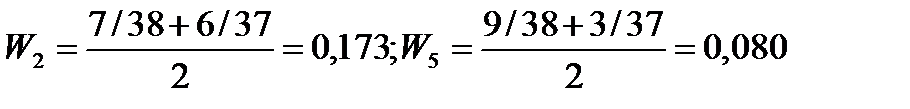
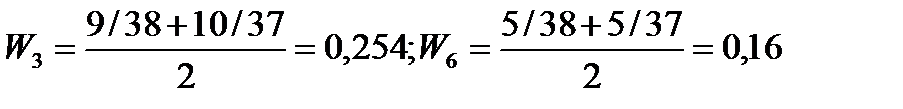
Нетрудно убедиться, что полученные усредненные оценки подчиняются трем основным правилам приписания оценок событиям (факторам, альтернативам). Сумма равна единице, каждая меньше единицы.
Каждая экспертная оценка может проводится с учетом и без учета компетентности экспертов. В том случае, когда компетентность экспертов учитывается, оценка умножается на значение соответствующего коэффициента компетентности КK.
При наличии нескольких, качественно различающихся целей (факторов) обычно рассчитывается комплексная оценка, которая определяется как средняя арифметическая с учетом веса (значимости) каждого отдельного фактора по формуле:
S = W1O1 + W2O2 + ... + Wn On,
где W1 , W2 , ... , Wn - веса (значимость) отдельных факторов;
O1 , O2 , ... , On - оценка факторов.
Предположим, что нужно выбрать один из двух возможных вариантов производственной программы П1 и П2, причем имеется две основные цели: Ц1 - увеличение производственной программы и Ц2 - сокращение времени производства 1 тонны продукции.
Представим, что если применить вариант П1, то годовая производительность возрастет на 100 тыс. руб, а время производства 1 тонны продукции уменьшится (по сравнению с фактическим), на 2 дня, если же принять вариант программы П2, то производительность возрастет на 200 тыс.руб, а время производства уменьшится на 1 день. Что предпочтительнее?
Для того, чтобы рассчитать общую эффективность каждого из вариантов, представляется разумным сложить "взвешенные" с учетом поставленных целей эффекты.
Однако это можно сделать лишь в том случае, если удастся установить соотношение между единицами увеличения годовой производительности с единицами уменьшения сроков производства продукции.
Например, если уменьшение срока на 1 день равнозначно 50 тыс. руб, то общий эффект для варианта программы П1 составит: 100000 + 2 х 50000 = 200000 , а для варианта П2: 200000 + 50000 = 250000.
Ясно, что вариант П2 в этих условиях будет предпочтительнее.
Таким образом, основные шаги для измерения общей эффективности при выборе предпочтительного решения заключается в следующем:
1) определяется эффект осуществления каждого из вариантов решения по отношению к каждой цели;
2) если полученные эффекты окажутся качественно различными, то они приводятся к общей мере эффективности;
3) суммируются эффекты для каждого варианта решения в целях получения оценки общей эффективности.
Ситуацию, возникшую при наличии нескольких целей, удобно представить в виде специальных таблиц, называемых матрицами решений.
В табл. приводится матрица решений для данных предыдущего примера.
Таблица. Матрица оценки общей эффективности
| Программы (решения) | ЦЕЛИ | Общая эффективность | |
| Ц1 | Ц2 | ||
| П1 | 2 х 50000 | ||
| П2 |
Наибольшие трудности при оценке альтернативных плановых решений встречаются в тех случаях, когда противоречивые цели выражаются в существенно различных единицах измерения, которые нельзя перевести в рубли. В таких случаях можно с помощью экспертов установить относительную важность (значимость) целей, а затем рассчитать взвешенный эффект (результат) с учетом каждой из целей.
Дата добавления: 2017-03-29; просмотров: 4742;
