Многокритериальный выбор на основе экспертных оценок
Постановка задачи многокритериального выбора. Будем предполагать, что множество X = {x1, x2, … xm} альтернативных решений сформировано тем или иным методом генерации альтернатив (методами мозгового штурма, морфологического анализа, сценариев, деловых игр и др.). Необходимо выбрать одну (или несколько) наиболее предпочтительных альтернатив. Для выбора наилучшего альтернативного решения из исходного множества X необходимо сформировать критерий выбора. Большинство методов выбора предполагают, что каждую альтернативу возможно оценить по критерию определенным числом (значением критерия). Наилучшей считается альтернатива, имеющая наилучшее значение критерия. Для большинства задач выбора невозможно использовать какой-либо один критерий. В этом случае используют несколько критериев Fi, 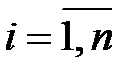 , описывающих одно решение с разных сторон и дополняющих друг друга. Такие критерии будем называть частными.
, описывающих одно решение с разных сторон и дополняющих друг друга. Такие критерии будем называть частными.
Рассмотрим пример. При выборе конструкции самолета проектировщикам следует учитывать множество критериев: технических (высотность, скорость, маневренность, грузоподъемность и т.д.), технологических (связанных с будущим процессом серийного производства), экономических (затраты на производство, обслуживание и т.д.), эргономических и пр.
Выбор по одному критерию сводится к отысканию альтернативы с наилучшим значением этого критерия. Многокритериальные задачи не имеют однозначного общего решения. Теоретически можно представить себе случай, когда имеется одна альтернатива, обладающая наилучшими оценками по всем критериям; она и является наилучшей. Однако на практике такие случаи встречаются редко. Часто по одному критерию наилучшей является одна альтернатива, по другому – другая.
Наиболее употребительным способом решения многокритериальной задачи является сведение ее к однокритериальной. Это означает введение интегрального критерия (суперкритерия) F, зависящего от частных критериев Fi, 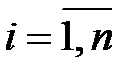 :
:
F = F (F1, F2, … Fn)
Оценка альтернативы по интегральному критерию, таким образом, зависит от ее оценок по каждому частному критерию, т.е. интегральная оценка каждой альтернативы есть некоторая функция от оценок по частным критериям
При определении интегральной оценки, кроме того, необходимо учитывать вклад каждого частного критерия в интегральный критерий. Дело в том, что частные критерии могут иметь разный вес (важность, ценность). Например, при проектировании гражданского самолета такой критерий, как надежность, является более важным, чем маневренность.
Будем рассматривать формирование интегрального критерия для частного случая. Предположим, что каждую альтернативу xj возможно оценить по критерию Fi числом в интервале от 0 до 1. Как правило, оценки выставляются экспертом или лицом, принимающим решения (ЛПР).
Важность частных критериев Fi будем оценивать коэффициентами важности wi, отражающими относительный вклад критериев в суперкритерий. Множество весовых коэффициентов частных критериев W = { w1, w2, … wn }, как правило, определяется экспертом (ЛПР) и отражает его личные предпочтения.
В дальнейшем будем предполагать, что весовые коэффициенты задаются положительным числом и сумма всех коэффициентов должна быть равна некоторой константе a, равной, например 1 (10, 100, 1000):
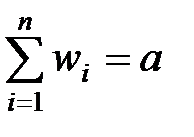
Ниже рассмотрены наиболее часто используемые виды интегральных критериев.
1) Максимум суммы взвешенных оценок:
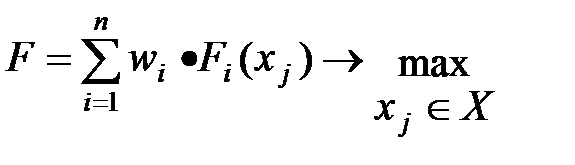
Наилучшей является альтернатива с максимальной суммой взвешенных оценок по всем частным критериям. Это наиболее распространенный критерий.
При максимальной оценке варианта по некоторому критерию, равной единице, его взвешенная оценка будет равна его весу. Таким образом, множество весов всех частных критериев характеризует идеальный возможный вариант.
Достоинство данного критерия заключается в его простоте и наглядном физическом смысле. Недостатком является следующее: можно получить относительно высокое значение интегрального критерия за счет больших значений отдельных частных критериев и малых значений других частных критериев.
2) Минимум суммы отклонений от «идеальной точки»:
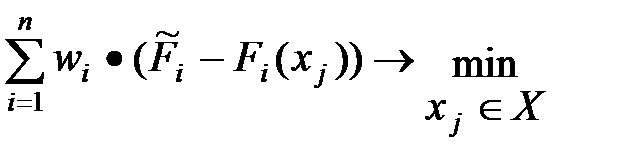
Наилучшей является альтернатива с минимальным отклонением взвешенных оценок от максимальных значений частных критериев ( 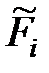 ), т.е. наиболее приближенная к идеалу по всем критериям (к «идеальной точке»). В нашем случае «идеальной точкой» будет альтернатива со следующими значениями частных критериев:
), т.е. наиболее приближенная к идеалу по всем критериям (к «идеальной точке»). В нашем случае «идеальной точкой» будет альтернатива со следующими значениями частных критериев:
F1 = F2 = … = Fn = 1
Очевидно, что оптимальное решение, найденное по критерию (2) совпадает с оптимальным решением, найденным по критерию (1).
3) Минимум суммы квадратов отклонений от «идеальной точки»:
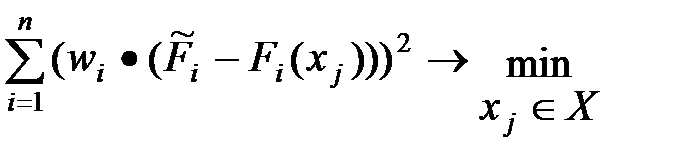
Этот интегральный критерий является более чувствительным к отклонениям. Критерий (3) позволяет «отсеять» альтернативы со значительными отклонениями значений частных критериев от их максимальных значений, т.к. такие отклонения, возведенные в квадрат, резко ухудшают значение интегрального критерия.
В отличие от предыдущих видов интегрального критерия, здесь альтернатива должна «равномерно» приближаться к идеалу.
4) Минимум максимального отклонения:
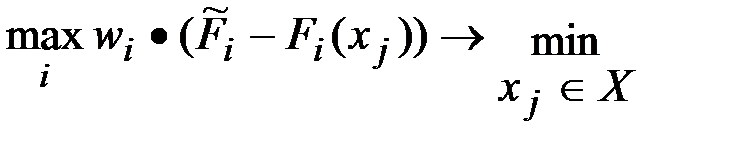
Этот критерий позволяет «отбраковывать» альтернативы с большими отклонениями по отдельным критериям.
5) Максимум минимальной оценки:
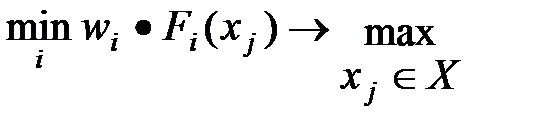
Для каждой альтернативы сначала находится минимальная взвешенная оценка по всем критериям. Наилучшей альтернативой является та, которая имеет максимальную оценку из минимальных оценок критериев. Этот критерий используется при выборе, когда нежелательны малые значения по частным критериям.
Рассмотрим пример выбора альтернативного варианта организационной структуры по интегральным критериям различных видов.
Множество X включает следующие альтернативы:
x1 – простая структура,
x2 - функционально-ориентированная структура,
x3 - структура на основе автономных центров (дивизиональная),
x4 - матричная структура.
Оценка каждого решения ведется по 9-ти частным критериям 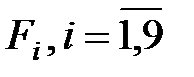 , приведенным в таблице .
, приведенным в таблице .
Коэффициенты wi, отражающие «вес» частных критериев, приведены в таблице. Их сумма равна 100.
Вариантам экспертами выставляются качественные оценки от "неудовлетворительно" до "отлично". Экспертным оценкам сопоставляются числовые оценки по следующей схеме:
· отлично (о) = 1,0;
· очень хорошо (ох) = 0,75;
· хорошо (х) = 0,625;
· удовлетворительно (у) = 0,5;
· посредственно (п) = 0,25;
· неудовлетворительно (н) = 0.
В таблице приведены значения интегральных критериев для альтернатив.
| Критерии | wi | x1 | x2 | x3 | x4 |
| F1 - Возможность компетентного управления | н | у | х | х | |
| F2 - Оперативность управления | н | н | ох | у | |
| F3 - Контролируемость работы подразделений | н | х | х | о | |
| F4 - Координируемость решений | х | у | у | п | |
| F5 - Адаптивность оргструктуры к изменению рынка | о | ох | о | х | |
| F6 - Затраты на административный аппарат | у | у | х | п | |
| F7 - Возможность технологического развития | о | х | о | ох | |
| F8 - Мотивация работы сотрудников | н | п | х | ох | |
| F9 - Ответственность подразделений за издержки и доходы | н | у | о | о | |
| Значения интегрального критерия (1) | 41,9 | 50,6 | |||
| Значения интегрального критерия (2) | 58,1 | 49,4 | |||
| Значения интегрального критерия (3) | 53,3 | 27,9 | 8,9 | 18,1 | |
| Значения интегрального критерия (4) | 11,2 | 7,5 | 11,2 | ||
| Значения интегрального критерия (5) | 3,1 | 1,2 |
Из таблицы видно, что по всем интегральным критериям оптимальным является вариант x3 – орг.структура на основе автономных центров. Естественно, что при решении других задач оптимальные варианты по разным интегральным критериям могут быть различными.
Метод Дельфи
Метод Дельфи представляет собой много туровую процедуру анкетирования с обработкой и сообщением результатов каждого тура экспертам, работающим отдельно друг от друга. Этот метод был разработан Хелмером и Гордоном (США) в середине 50-х годов для составления всевозможных прогнозов. Экспертам предлагается ответить на ряд вопросов и свои ответы аргументировать. При этом какие-либо дискуссии между экспертами запрещены, что, по мнению авторов метода, исключает роль психологических и эмоциональных факторов, неизбежно проявляющихся во время открытой дискуссии.
Полученные от эксперта данные обрабатываются с целью выделения среднего или медианы и крайних значений оценок. Экспертам сообщаются результаты обработки первого тура опроса с указанием расположения оценок каждого эксперта. Если оценка эксперта сильно отклоняется от среднего значения, то его просят аргументировать свое мнение или изменить оценку.
Во втором туре эксперты аргументируют или изменяют свою оценку с объяснением причин корректировки. Результаты опроса во втором туре обрабатываются и сообщаются экспертам. Если после первого тура производилась корректировка оценок, то результаты обработки второго тура содержат новые средние и крайние значения оценок экспертов. В случае сильного отклонения своих оценок эксперты должны аргументировать или изменить свои суждения, пояснив причины корректировки. Проведение последующих туров осуществляется по аналогичной процедуре. Обычно после третьего или четвертого тура оценки экспертов стабилизируются, что и служит критерием прекращения дальнейшего опроса.
Итеративная процедура опроса с сообщением результатов обработки после каждого тура обеспечивает лучшее согласование мнений экспертов, поскольку эксперты, давшие сильно отклоняющиеся оценки, вынуждены критически осмыслить свои суждения и обстоятельно их аргументировать. Необходимость аргументации или корректировки своих оценок не означает, что целью экспертизы является получение полной согласованности мнений экспертов. Конечным результатом может оказаться выявление двух или более групп мнений, отражающих принадлежность экспертов к различным научным школам, ведомствам или категориям лиц. Получение такого результата является также полезным, поскольку позволяет выяснить наличие различных точек зрения и поставить задачу проведения исследований в данной области.
Дата добавления: 2017-03-29; просмотров: 1178;
