Методы экспертных оценок
При исследовании сложных систем возникают проблемы, выходящие за пределы формальных математических постановок задач. В таком случае прибегают к услугам экспертов, т.е. лиц, чьи суждения и интуиция могут уменьшить сложность проблемы. Обсудим вопросы привлечения экспертов к решению конкретной и частной задачи системного анализа – задачи выбора. Правда, в этой частной задаче имеются и некоторые общие черты экспертных методов (например, подходы к оценке компетентности экспертов, к интерпретации даваемых ими результатов и пр.).
Основная идея экспертных методов состоит в том, чтобы использовать интеллект людей, их способность искать и находить решение слабо формализованных задач. Однако особенность интеллектуальной деятельности людей состоит в том, что она во многом зависит от внешних и внутренних условий. Поэтому в методиках организации экспертных оценок специальное внимание уделяется созданию благоприятных условий и нейтрализации факторов, неблагоприятно влияющих на работу экспертов.
Простейший вариант состоит в следующем. Если эксперты предлагают различающиеся упорядочения альтернатив, то возникает вопрос о том, как использовать мнения всех экспертов для окончательного упорядочения. Это далеко не тривиальная задача. Фактически мы возвращаемся к проблеме коллективного выбора со всеми его особенностями, в том числе – с возможностями парадоксов .
Предположим, например, что эксперты оценивают альтернативы в числовых шкалах. Пусть qj(xi) – оценка i-й альтернативы j-м экспертом ( 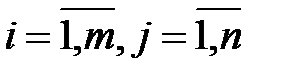 ). Оценки q1(xi), ..., qn(xi) можно рассматривать как “измерения” искомой “истинной характеристики” q(xi), считая отклонения qj(xi) – q(xi) случайными величинами. В качестве приближения можно использовать некоторую статистику
). Оценки q1(xi), ..., qn(xi) можно рассматривать как “измерения” искомой “истинной характеристики” q(xi), считая отклонения qj(xi) – q(xi) случайными величинами. В качестве приближения можно использовать некоторую статистику 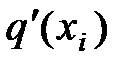 =
= 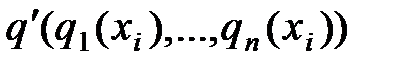 ; обычно это выборочное среднее
; обычно это выборочное среднее
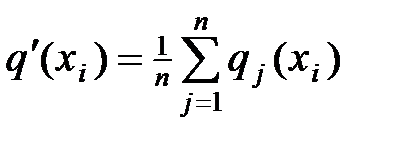 .
.
Сложнее обстоит дело, когда альтернативы нельзя оценить сразу одним числом и экспертам предлагается дать оценки отдельно по каждому показателю. Например, оценка качества промышленного изделия складывается из оценок признаков социальных (уровень потребности), функциональных (степень соответствия назначения), экономических, эстетических, эргономических и др. В этом случае имеем набор чисел qjk(xi), где k – номер признака. Кроме этих чисел экспертов просят оценить степень важности jkкаждого показателя (если это не выполнено другим способом). Тогда
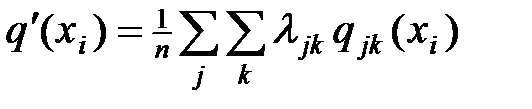 .
.
Следующее уточнение вводят в случае неоднородности группы экспертов. Естественно придать различные (а не одинаковые, равные 1/n) веса мнениям экспертов, имеющих разную квалификацию. Определение коэффициента jкомпетентности j-го эксперта можно поручить самим экспертам. Пусть каждый из них (l-й) оценивает компетентность других числами 0 £ lj £ 1 (при этом и свою – числом ll). Усреднение дает 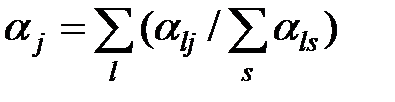 . В результате получают итоговую оценку
. В результате получают итоговую оценку 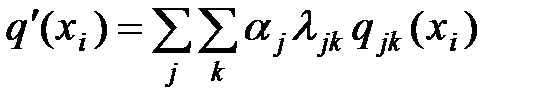 .
.
В тех случаях, когда эксперты лишь упорядочивают альтернативы, т.е. используют только порядковую шкалу, возможность арифметических операций отпадает. Существуют специальные методы обработки экспертной информации, измеренной в нечисловых шкалах (назывных, шкалах порядка).
Представим, что три эксперта должны про ранжировать три основных фактора, влияющих на выбор планового варианта производства какого-то изделия, и что этими факторами являются ожидаемая прибыль, срок выполнения и техническая новизна.
Предположим, что каждому из этих факторов эксперты присвоили в соответствии со своими представлениями об их значимости ранги, (см. табл., первые три строки). Таким образом, исходя из таблицы, наивысший результирующий ранг - 1 присвоен фактору "Техническая новизна", получившему минимальную сумму рангов и являющемуся, таким образом с точки зрения группы экспертов, наиболее важным при выборе планового варианта. Последующие результирующие ранги (2, 3, 4) установлены в зависимости от суммы рангов, полученной другими факторами.
Таблица. Ранжирование экспертами факторов, влияющих на выбор планового варианта
| Эксперты | ФАКТОРЫ | |||
| Ожидаемая прибыль | Срок выполнения | Техническая новизна | Уровень затрат | |
| Э1 | ||||
| Э2 | ||||
| Э3 | ||||
| Сумма рангов | ||||
| Результирующий ранг |
Иногда для установления результирующего ранга сначала рассчитывается средний ранг путем деления суммы рангов на число экспертов, а затем уже по величине среднего ранга устанавливается результирующий.
Точность и надежность процедуры ранжирования в значительной степени зависит от количества оцениваемых объектов (факторов, альтернатив). В принципе чем таких объектов меньше, тем выше их различимость с точки зрения экспертов, а, следовательно, надежнее полученные оценки. Практика показывает, что количество ранжируемых объектов не должно быть больше 20, но наиболее надежна эта процедура, когда оно меньше 7.
Вместе с тем ранг определяет лишь место, занимаемое каждым объектом среди других. Как далеко отстоят друг от друга сравниваемые объекты, метод ранжирования ответа не дает.
На практике метод ранжирования в чистом виде используется редко. Чаще - в сочетании с другими методами упорядочивания. Так ранжирование может быть использовано для оценки значимости объектов в сочетании с методом непосредственной оценки.
Дата добавления: 2017-03-29; просмотров: 698;
