Полный факторный эксперимент
В большинстве случаев при проведении опытов факторы поддерживают на 2-х уровнях (верхнем и нижнем) [3]. Если число уровней m, а число факторов k, то общее число опытов в эксперименте 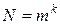 , но большинство опытов проводится на двух уровнях, т.е. при m=2, то в этом случае число опытов, которые надо провести, равно 2k. Если мы имеем два фактора, т.е. k=2, то число опытов N=4. Если число факторов k=3, то число опытов равно 8.
, но большинство опытов проводится на двух уровнях, т.е. при m=2, то в этом случае число опытов, которые надо провести, равно 2k. Если мы имеем два фактора, т.е. k=2, то число опытов N=4. Если число факторов k=3, то число опытов равно 8.
Полным факторным экспериментомназывается такой эксперимент, при котором проводятся опыты при всех сочетаниях уровней факторов. Цель первого этапа планирования экстремального эксперимента – получение линейной модели. Он предусматривает варьирование факторов на двух уровнях.
Факторный эксперимент реализуют с помощью матрицы планирования,в которой используют кодированные значения факторов. Так, например, для двух и трех факторов полный факторный эксперимент типа 2k можно представить матрицами, приведенными в табл. 2.1.
Число строк в матрице равно количеству опытов. Знаками +1 и –1 обозначают верхний и нижний уровни факторов X1, Х2 и Х3 в опытах. Значения функции отклика, полученные при выполнении опытов, обозначены через Y.
Для упрощения записи условий эксперимента в матрице планирования вместо +1 пишут только « + », а вместо –1 - только «–».
При k=2, моделью первой степени будет уравнение регрессии вида 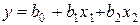 .
.
Значения коэффициентов в этом уравнении определяют с помощью значений функции отклика, полученных в результате опытов.
Таблица 2.1
Матрицы полного факторного эксперимента типа 22
| Номер опыта | X1 | Х2 | Y | Номер опыта | X1 | Х2 | X1 Х2 | Y |
| – | – | Y1 | + | – | – | Y1 | ||
| + | – | Y2 | + | + | + | Y2 | ||
| – | + | Y3 | – | + | – | Y3 | ||
| + | + | Y4 | – | – | + | Y4 |
Дата добавления: 2019-10-16; просмотров: 638;
