Опыты, повторенные несколько раз при одних и тех же значениях факторов, называют параллельными.

Под дублированием опытов понимают постановку параллельных опытов.

Обычно число п параллельных опытов принимают равным 3, иногда 4 или 5. При проведении исследований приходится иметь дело с тремя вариантами дублирования:

1) эксперимент проведен при равномерном дублировании опытов;

2) эксперимент выполнен при неравномерном дублировании опытов;

3) эксперимент поставлен без дублирования опытов.

При равномерном дублировании все строки матрицы планирования имеют одинаковые числа параллельных опытов. В случае неравномерного дублирования числа параллельных опытов неодинаковы.

При отсутствии дублирования параллельные опыты не проводятся.

Наиболее предпочтительным из трех вариантов дублирования является первый. При этом варианте эксперимент отличается повышенной точностью, а математическая обработка экспериментальных данных - простотой. По этой причине мы будем использовать первый вариант дублирования опытов.

Рассмотрим методику обработки результатов эксперимента для первого варианта дублирования опытов.

Обработка результатов эксперимента при равномерном дублировании опытов проводятся в последовательности, изложенной ниже.Длякаждой строки матрицы планирования по результатам п параллельных опытов находят среднее арифметическое значение параметра оптимизации:

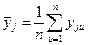, (2.11)

где и - номер параллельного опыта; 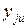– значение параметра оптимизации в и-том параллельном опыте j-той строки матрицы.

С целью оценки отклонений параметра оптимизации от его среднего значения для каждой строки матрицы планирования вычисляют дисперсию 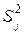опыта по данным п параллельных опытов.

Статистической дисперсией называют среднее значение квадрата отклонений случайной величины от ее среднего значения:

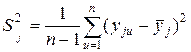. (2.12)

Ошибка S_j опыта определяется как корень квадратный из дисперсии опыта:

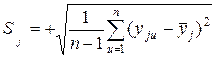. (2.13)