Уравнение непрерывности

Рассмотрим локальный объем полупроводника с одиночной площадью S=1 см² и толщиной dx. Объем такой области будет равен V=S·dx=dx рис. 2.8. Пусть n(x,t) – концентрация электронов в этой области. Общее количество электронов в этой области будет равно n_(x,t)dx. Изменение количества электронов в этой локальной области за время dt будет равно:

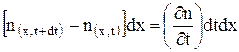. (2.7.1)

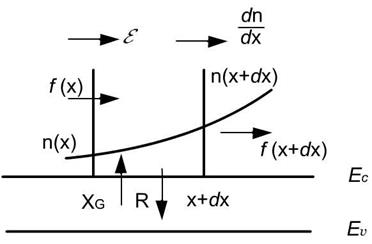
Рис. 2.8

Изменение количества электронов может происходить вследствие действия следующих процессов:

- термической генерации n_G=G×dt×dx – где G – скорость генерации;

- рекомбинации носителей n_R=-R×dt×dx;

- разностью входящего и выходящего потоков электронов в локальную область и из нее под действием электрического поля и градиента концентрации:

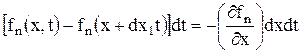. (2.7.2)

Общее изменение концентрации электронов будет равно:

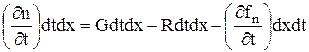, (2.7.3)

тогда

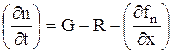. (2.7.4)

Плотность тока электронов равна j_n=-f_nq, следовательно, f_n=- .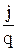

Тогда 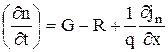. (2.7.5)

Это выражение называется уравнением непрерывности. Плотность тока j_n в общем случае складывается из дрейфовой и диффузионных составляющих.

Пусть j_n=0, тогда .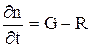

В равновесном состоянии G=R .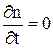

В неравновесном состоянии G ≠ R.

Обозначим G-R= 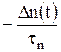, где Δn_(t) избыточная концентрация электронов, являющаяся функцией времени. Подставив в (2.7.5) получим:

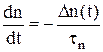
Решение этого уравнения будет иметь вид ,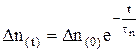

где Δn₍₀₎ – избыточная концентрация в начальный момент времени.

Величину τ_n называют временем жизни носителей, в данном случае электронов. Это среднее время, в течение которого избыточная концентрация уменьшается в е раз вследствие рекомбинации.