Уровень Ферми и равновесная концентрация носителей в невырожденных собственных полупроводниках

Если в полупроводнике нет примесей, так что N_A=N_D=0, где N_A и N_D - концентрации соответственно акцепторной и донорной примесей, то такой полупроводник называется собственным или чистым. В собственных полупроводниках концентрация электронов в зоне проводимости n_i равна концентрации дырок в валентной зоне p_i.

n_i=p_i (2.3.1)

Индексами «i» обозначают равновесные концентрации в собственных полупроводниках. Приравнивая правые части соотношений (2.2.4) и (2.2.5) получаем

,

,

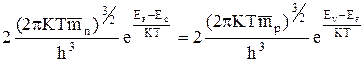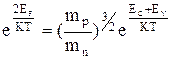откуда 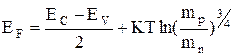. (2.3.2)

Это соотношение определяет положение уровня Ферми в собственных полупроводниках. При абсолютном нуле Т=0:

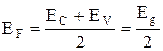, (2.3.3)

где Eg - ширина запрещенной зоны. Т.е. при Т=0 уровень Ферми располагается посередине запрещенной зоны.

С повышением температуры он смещается вверх к дну зоны проводимости, если m_p>m_n и вниз если m_p<m_n (рис. 2.4). Однако, в большинстве случаев это смещение настолько незначительно, что им можно пренебречь и считать, что уровень Ферми в собственных полупроводниках располагается по середине зоны.

Если подставить E_F из (2.3.3) в (2.2.4) и (2.2.5), то получим

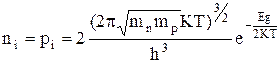. (2.3.4)

Из (2.3.4) следует, что равновесная концентрация носителей заряда в собственном полупроводнике определяется шириной запрещенной зоны E_g. При чем зависимость n_i от T и E_g очень сильная.

Из (2.3.4) можно получить:

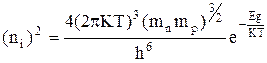. (2.3.5)

Правые части (2.3.5) и (2.2.6) равны , следовательно, равны и левые

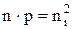. (2.3.6)

Это выражение также выражает закон действующих масс. Из (2.3.6) следует, что концентрация электронов и дырок в любом невырожденном полупроводнике таковы, что их произведение равно квадрату собственной концентрации электронов. Соотношение (2.3.6) справедливо при любой температуре

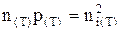. (2.3.7)