Зависимость концентрации свободных носителей в полупроводнике от положения уровня Ферми

В отличие от металлов, в которых электронных газ является вырожденным и подчиняется статистике Ферми-Дирана, в собственных и слаболегированных примесных полупроводниках электронный (дырочный) газ является невырожденным и распределение электронов по состояниям описывается классической статистикой Максвелла-Больцмана. Для таких полупроводников концентрация свободных носителей зависит от положения уровня Ферми и температуры Т.

При температуре отличной от нуля в зоне проводимости полупроводника находятся электроны и в валентной зоне дырки. Обозначим их концентрацию через n и р.

Определим равновесную концентрацию электронов проводимости в зоне проводимости. При этом за нулевой уровень отсчета энергии электронов принимается потолок валентной зоны.

Концентрацию электронов , энергия которых заключена в интервале от Е до E+dE можно выразить следующим образом

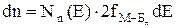, (2.2.1)

где Nn(E) - число элементарных фазовых ячеек или состояний, приходящихся на единичный интервал энергии;

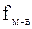- функция распределения Максвелл-Больцмана ( 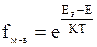), выражающая вероятность заполнения электроном с энергией Е фазовой ячейки.

Множитель 2 выражает принцип Паули.

Как нам известно .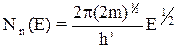

Тогда (2.2.1) можно записать в виде 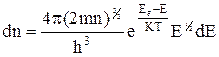. (2.2.2)

Полное число электронов n , находящихся при температуре Т в зоне проводимости, можно получить интегрируя (2.2.2) по всем значениям энергии соответствующим зоне проводимости

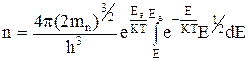. (2.2.3)

Проинтегрировав (2.2.3) получим

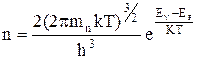. (2.2.4)

Если провести подобный расчет для дырок, то можно получить аналогичное выражение

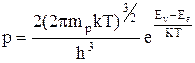. (2.2.5)

В (2.2.4) и (2.2.5) m_n и m_p эффективные массы дырок и электронов.

Из выражений (2.2.4) и (2.2.5) следует, что концентрация свободных носителей заряда в данной зоне определяется расстоянием этой зоны от уровня Ферми E_F, чем больше это расстояние, тем ниже концентрация носителей.

Произведение n на р для любого невырожденного полупроводника равно

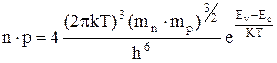. (2.2.6)

Это формула показывает, что при фиксированной температуре произведение концентраций электронов и дырок для данного полупроводника является величиной постоянной. Соотношение (2.2.6) выражает так называемый закон действующих масс в применении к газу свободных носителей в полупроводниках.

Рис. 2.3

Рис. 2.4