Эффективная масса электрона

Известно:

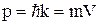, (1.3.1)

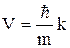. (1.3.2)

Кинетическая энергия свободного электрона равна E_k=E

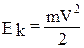. (1.3.3)

Подставим (1.3.2)

тогда 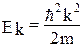(1.3.4)

E

D1

D

C

C1

B

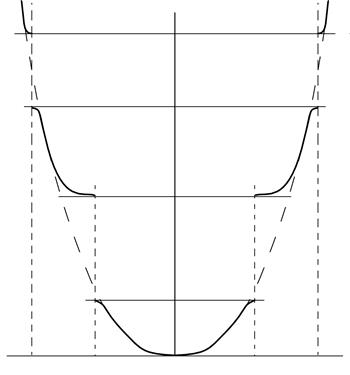
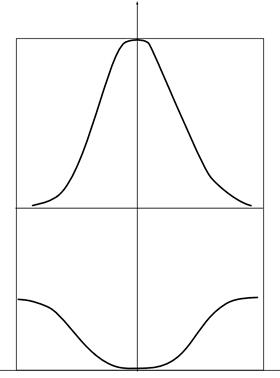
Рис. 1.6

	D1
			D

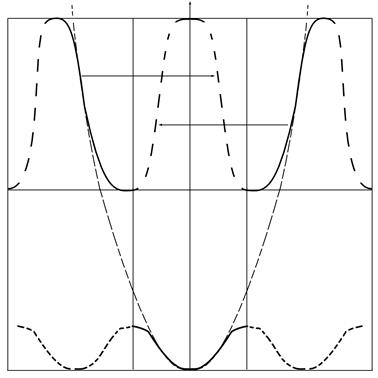
Рис. 1.7

		E
	-p/ax

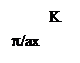Рис. 1.8

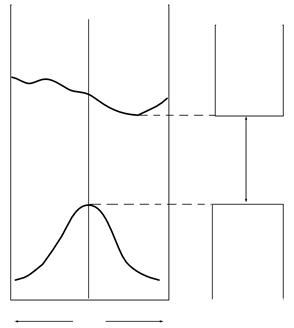
Рис. 1.9

Продифференцируем E_k по k:

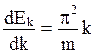, (1.3.5 )

отсюда 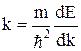. (1.3.6)

Подставим (1.3.6) в (1.3.2)

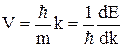. (1.3.6)

Формула (1.3.6) справедлива не только для свободного электрона, но и для электрона, находящегося в потенциальном поле.

Пусть энергия зонного электрона изменяется под некоторым внешним воздействии.

dE=FVdt . (1.3.7)

где F - внешняя сила

Подставим (1.3.6) в (1.3.7)

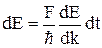, (1.3.8)

отсюда 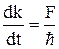. (1.3.9)

Продифференцируем (1.3.6) по времени

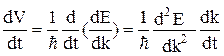. (1.3.10)

Подставим (1.3.9) в (1.3.10)

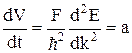. (1.3.11)

где а - ускорение.

Формула (1.3.11) связывает ускорение и силу, т.е. она выражает второй закон Ньютона F=ma; a=F/m.

Из (1.3.11) следует, что под действием внешней силы электрон в периодическом поле кристалла движется так, как двигался бы свободный электрон, обладающий массой

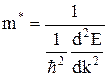. (1.3.12)

Масса m* называется эффективной массой электрона. Приписывая электрону, находящемуся в периодическом поле кристалла массу m*, мы можем считать этот электрон свободным и описывать его движение во внешнем поле так, как описывается движение свободного электрона. Эффективная масса, отражающая особенности движения электрона в периодическом поле, является своеобразной функцией. Она может быть как положительной, так и отрицательной, а по абсолютному значению как меньше, так и больше массы покоя электрона. Эффективная масса свободного электрона равна массе покоя.

При движении электрона в периодическом потенциальном поле кристалла работа внешней силы может переходить как в кинетическую, так и потенциальную энергию электрона.

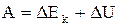. (1.3.13)

Если часть работы внешней силы F=-qe переходит в потенциальную энергию, то скорость электрона возрастает медленнее, чем у свободного электрона и следовательно его эффективная масс больше массы покоя. Если вся работа внешней силы переходит в потенциальную энергию, то скорость электрона изменяться не будет, и он будет вести себя, как частица с бесконечно большой массой.

В потенциальную энергию может переходить не только работа внешней силы, но и кинетическая энергия электрона. Скорость электрона будет в этом случае уменьшаться, т.е. он ведет себя как частица с отрицательной массой.

Возможен случай, когда в кинетическую энергию может переходить не только работа внешней силы, но и потенциальная энергия, тогда скорость электрона будет расти быстрее, чем у свободного, т.е. его эффективная масса будет меньше массы покоя. На рис. 1.10 показаны зависимости E, V, m* от волнового вектора k. Вблизи дна разрешенной зоны энергия m* электрона положительна, а у потолка зоны отрицательна. Точка А - точка перегиба зависимости E(k), в этой точке 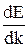достигает максимума, а вторая производная 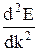равна 0, а m*®¥. Поскольку k вектор, то m* зависит от направления движения электрона в кристалле.