Понятие о стабилизации систем

Основным путем разрешения противоречия между точностью и устойчивостью систем является изменение структуры системы, наложение дополнительных связей.

Дополнительные связи необходимы как для стабилизации системы, так и для получения требуемого качества регулирования.

Рассмотрим структурную схему САУ с передаточной функцией.

,

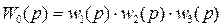где 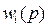- передаточные функции чистой системы

Рис.5.5 Типы дополнительных связей

Эти части сами могут быть сложными системами звеньев.

Если в целях обеспечения устойчивости или для других требований в систему вводится некоторая дополнительная часть, то она называется дополнительной связью. Дополнительные связи называются также стабилизирующими устройствами или корректирующими цепями.

Дополнительные звенья могут подключаться к основным частям системы последовательно, параллельно и антипараллельно.

На рисунке 5.5 показаны различные возможные способы параллельного включения звена дополнительной связи к цепочке последовательно соединенных основных звеньев систем.

Выход звена I подключен ко входу звена с передаточной функцией w₁(p). Если воздействие с помощью дополнительной связи I передается назад по тракту системы, то звено I называют звеном обратной связи. Звено II, подающее воздействие с выхода звена w₁(p) на вход следующего звена, является звеном прямой связи. Точно также звенья III и IV являются звеньями прямой связи.

Так как в реальных системах предшествующие звенья обладают меньшей мощностью, чем последующие, то связи III и IV обычно не применяются.

В общем случае передаточная функция дополнительного звена (связи) имеет вид:

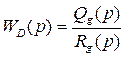, (1)

где Q и R – многочлены полинома.

Если 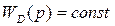, т.е. дополнительная связь будет усилительным звеном, то она называется идеальной жесткой связью.

Если 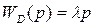, т.е. является дифференцирующим звеном, то связь называется идеальной гибкой связью.

Звено с передаточной функцией 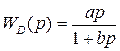называют реальной гибкой связью.

Если гибкая связь подключена так как звено II, то она называется форсирующей связью(рис.5.6).

Рис.5.6 Схема форсирующей связи

В этом случае можно представить себе эту связь совместно с основным воздействием x_n как некоторое звено, на вход которого подается величина x_n, на выходе оказывается величина

.

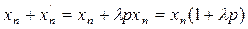Следовательно передаточная функция подобного звена имеет вид в случае идеальной форсирующей связи

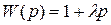, (2)

где W(p) – передаточная функция форсирующего звена.

Это звено D является примером последовательной дополнительной связи, включаемой последовательно в тракт системы.

Передаточная функция W₂(p) любой последовательной связи может иметь сколь угодно сложный вид, но дополнительное звено должно пропускать постоянное по величине воздействие.

Поэтому при единичной функции, поданной на вход дополнительного звена установившееся значение его выходной величины 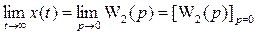не равно нулю. Передаточная функция (2) удовлетворяет этому ограничению.

Для любой параллельной дополнительной связи 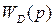при заданной передаточной функции 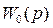основной цепи можно найти эквивалентную ей последовательную связь w₂(p).

Рис.5.7 Схема системы с дополнительной связью

1. Для системы на рисунке 5.7:

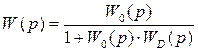
2. При последовательном соединении звеньев:

.

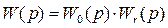Если эти схемы эквивалентны, то приравнивая правые части выражения найдем:

.

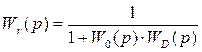Наоборот, по заданной передаточной функции последовательной связи можно найти эквивалентную ей параллельную связь. Решая последнее уравнение относительно 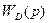, получим:

.

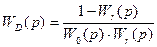Приведем пример форсирующей связи (рис.5.8).

Рис.5.8 Принципиальная схема форсирующей связи

Пусть х₀ и х – входное и выходное напряжение;

i_c – ток в цепи конденсатора с емкостью с;

i₁ – ток в цепи сопротивления R₁;

i₂ – ток в цепи сопротивления R₂.

Уравнение Кирхгофа для цепи имеет вид:

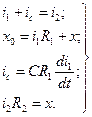
Запишем эти уравнения в операторном виде:

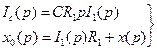
Исключая из этих уравнений все переменные кроме x(p) и x₀(p), найдем передаточную функцию звена:

,

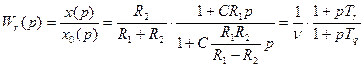где , , .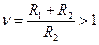

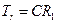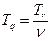Полученная передаточная функция w_r(p) отличается от передаточной функции идеальной форсирующей связи (w(p)=1+λp) и называется реальной форсирующей связью.

Найдем эквивалентную ей передаточную функцию обратной связи, шунтирующей, например, усилительное звено с передаточной функцией W₀(p)=k₀=const.

По формуле 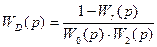найдем:

,

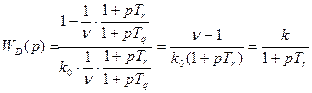где 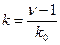; 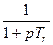– передаточная функция инерционного звена.

Такое звено можно получить с помощью схемы, состоящей из емкости с´ и сопротивления R´ и усилительного звена с коэффициентом усиления .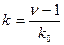

,

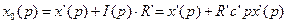
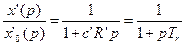где .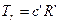

Вопросы для самопроверки

1. Для каких целей изменяют структуру системы, вводя дополнительные связи?

2. В каком случае звено дополнительной связи называется звеном обратной связи?

3. В каком случае звено дополнительной связи называется звеном прямой связи?

4. Какая дополнительная связь называется идеальной жесткой связью. Ее передаточная функция?

5. Записать передаточную функцию реальной гибкой связи, идеальной гибкой связи?

6. В каком случае гибкая связь называется форсирующей?

7. Записать передаточную функцию идеальной форсирующей связи?

8. Чему равно установившееся значение выходной величины дополнительного звена при единичном воздействии на его вход?

9. Записать передаточную функцию последовательной связи эквивалентную заданной передаточной функции параллельной дополнительной связи к основной цепи?

10. Записать передаточную функцию параллельной связи эквивалентно заданной передаточной функции последовательной связи, дополняющей основную цепь системы?

11. Записать выражения для относительной погрешности в установившемся режиме работы системы?