Понятие о стабилизации систем

К системам автоматического регулирования предъявляются требования устойчивости переходного процесса и точности (малой ошибки) в установившемся режиме. Эти два требования находятся в тесной связи друг с другом.

Рассмотрим работу системы автоматического регулирования, изображенной на рис.5.1.

Рис.5.1 Структурная схема САР

Дифференциальное уравнение, связывающее выход Х со входом Х₀ имеет вид:

,

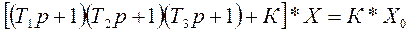где К=К₁*К₂*К₃,

К – коэффициент усиления

Т – время переходного процесса.

Пусть на вход системы подается ступенчатая функция Х₀ = С. Если система устойчивая, то после окончания переходного процесса регулируемая координата Х примет некоторое установившееся постоянное значение Х = Х_у.

Так как в установившемся режиме все производные от Х равны нулю, то из уравнения:

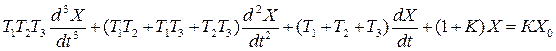(1)

Получим (1+К)Х_у=КС, откуда:

.

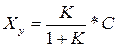Таким образом Х_у отличается от заданного значения Х₀=С.

Если ввести погрешность установившегося значения X_s, то можно записать:

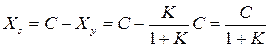
Тогда относительная погрешность S установившегося значения, которую называют коэффициентом статизма равна:

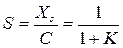. (2)

Системы, у которых существует установившаяся погрешность X_s, называются статическими.

Системы, в которых такая погрешность отсутствует, называются астатическими. Например, система, структурная схема которой приведена на рис.5.2 будет астатической.

Рис.5.2 Структурная схема астатической системы

Передаточные функции звеньев на этой схеме следующие:

;

;

.

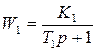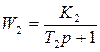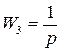Дифференциальное уравнение, описывающее связь Х с Х₀ имеет вид:

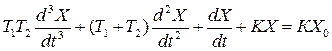, (3)

где К=К₁*К_2.

При Х₀ = С, получим Х_у = С. (4)

Так как в установившемся режиме все производные от Х равны нулю, установившаяся погрешность

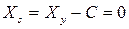. (5)

Т.е. чтобы система уравнения стала астатической, необходимо чтобы в замкнутом контуре системы находилось интегрирующее звено.

Из формулы (2) видно, что для уменьшения погрешности системы необходимо сделать коэффициент усиления системы К как можно больше.

Например, чтобы S была меньше 0,01 (1%), необходим К>99. Но при большом К система может стать неустойчивой.

Для системы управления, описываемой дифференциальным уравнением (1) необходимое условие устойчивости:

,

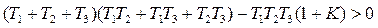из этого условия вытекает:

,

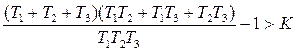т.е. предельное значение коэффициента усиления системы К = К_пр будет равно:

,

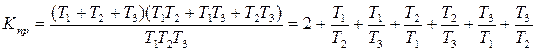т.е. К_пр зависит от постоянных времени отдельных звеньев системы. Например, если Т₁=Т₂=Т₃, то коэффициент К достигает К_пр= 8, что противоречит требованию малости величины статизма S.

Отсюда можно сделать вывод о существовании противоречия между требованием устойчивости и малой установившейся погрешностью.

Для увеличения К, т.е. получения меньшего коэффициента статизма, нужно изменять постоянные времени, что в реальных условиях не всегда можно сделать. Поэтому в систему добавляют новые устройства (дополнительные связи жесткие или гибкие), позволяющие достичь устойчивости при большом коэффициенте усиления.