Закон распределения дискретной случайной величины. Многоугольник распределения
Пусть X - дискретная случайная величина, которая принимает значения 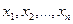 с некоторой вероятностью
с некоторой вероятностью 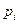 , где
, где  . Закон распределения дискретной случайной величины удобно задавать с помощью формулы
. Закон распределения дискретной случайной величины удобно задавать с помощью формулы 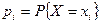 ,
,  определяющей вероятность того, что в результате опыта случайная величина X примет значение
определяющей вероятность того, что в результате опыта случайная величина X примет значение 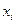 . Для дискретной случайной величины X закон распределения может быть задан в виде таблицы распределения:
. Для дискретной случайной величины X закон распределения может быть задан в виде таблицы распределения:
| X | x1 | x2 | … | xn | … |
| P | p1 | p2 | … | pn | … |
где первая строкасодержит все возможные значения (обычно в порядке возрастания)случайной величины,а вторая - их вероятности. Такую таблицу называют рядом распределения.
Так как события 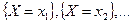 несовместны и образуют полную группу, то сумма их вероятностей равна единице, т.е.
несовместны и образуют полную группу, то сумма их вероятностей равна единице, т.е. 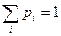 .
.
Закон распределения дискретной случайной величины можно задать графически, если на оси абсцисс отложить возможные значения случайной величины, а на оси ординат - вероятности этих значений. Ломаную, соединяющую последовательно точки (x1, p1), (x2, р2), … называютмногоугольником (или полигоном) распределения(см. рис. 5.1).
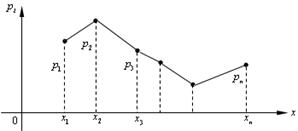
Рис. 5.1.
Теперь можно дать более точное определение дискретной случайной величины.
Случайная величина X дискретна, если существует конечное или счетное множество чисел 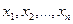 таких, что
таких, что 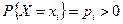 (
(  ) и
) и 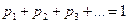 .
.
Определим математические операции над дискретными случайными величинами.
Суммой (разностью, произведением) дискретной случайной величины X, принимающей значения 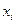 с вероятностями
с вероятностями 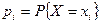 ,
, 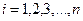 и дискретной случайной величины Y, принимающей значения
и дискретной случайной величины Y, принимающей значения 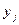 с вероятностями
с вероятностями 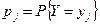 ,
, 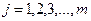 , называется дискретная случайная величина Z=X+Y (Z=X-Y, Z = X ∙ Y), принимающая значения
, называется дискретная случайная величина Z=X+Y (Z=X-Y, Z = X ∙ Y), принимающая значения 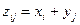 (
( 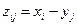 ,
, 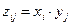 ) с вероятностями
) с вероятностями 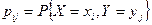 для всех указанных значений i и j. В случае совпадения некоторых сумм
для всех указанных значений i и j. В случае совпадения некоторых сумм 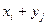 (разностей
(разностей 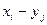 , произведений
, произведений 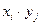 ) соответствующие вероятности складываются.
) соответствующие вероятности складываются.
Произведениедискретной случайной величины на число с есть дискретная случайная величина сХ, принимающая значения 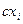 с вероятностями
с вероятностями 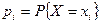 .
.
Две дискретные случайные величина X и Y называются независимыми, если события 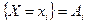 и
и 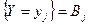 независимы для любых
независимы для любых 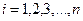 и
и 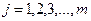 , т.е.
, т.е.
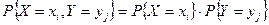 .
.
В противном случае случайные величины называются зависимыми.
Несколько случайных величин называются взаимно независимыми, если закон распределения любой из них не зависит от того, какие возможные значения приняли остальные величины.
Пример 5.1. В урне 8 шаров, из которых 5 белых, остальные - черные. Из нее вынимают наудачу 3 шара. Найти закон распределения числа белых шаров в выборке.
Решение:
Возможные значения случайной величины Х – числа белых шаров в выборке есть 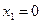 ,
, 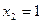 ,
, 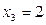 ,
,  . Вероятности их соответственно будут
. Вероятности их соответственно будут
 ,
, 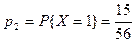 ,
,
 ,
, 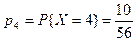 .
.
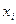
| 0 | 1 | 2 | 3 |
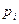
| 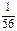
| 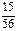
| 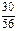
| 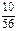
|
Контроль: 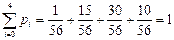 .
.
Дата добавления: 2017-03-29; просмотров: 307;
