Теоретические предпосылки решения задачи расчета надежности технической системы, резервированной по принципу нагруженного или «теплого» резерва.

До сих пор мы рассматривали системы, надежность дублирующих устройств которых не зависела от момента включения этих устройств в работу. Гораздо сложнее выглядит расчет надежности реальной системы, резервное устройство которой может отказывать до включения в работу с меньшей плотностью отказов, чем при включении в активное замещение отказавшего устройства.

Существенное повышение надежности может достигаться путем применения так называемого нагрузочного или «теплого» резервирования. В процессе проектирования сложных технических систем конструктор может во многих случаях уменьшить нагрузку на отдельные (резервные) устройства или элементы системы более чем в 10 раз по сравнению с нормальной. При этом интенсивность отказов резервных устройств остается постоянной во времени и, как правило, линейно убывает с уменьшением коэффициента нагрузки.

Сравнение показателей надежности систем, резервированных различными способами, показывает, что нагрузочное резервирование может быть более эффективным в системах, предназначенных для длительной работы в относительно стабильных условиях.

Допустим, что техническая система состоит из одного основного и одного резервного устройства, работающих «параллельно». Интенсивность отказов основного устройства обозначим через l₀(t). При отказе основного устройства происходит мгновенное безотказное автоматическое переключение работы на второе (резервное) устройство. Интенсивность потока отказов резервного устройства до его включения в работу обозначим через l₁(t). После включения резервного устройства в работу интенсивность потока его отказов мгновенно подскакивает (рис.5.1) до значения 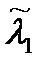, которую естественно полагать зависящей не только от текущего момента времени t, но и от того срока t₀, в течение которого элемент работал в облегченном режиме:

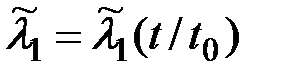(5.1)
Рассмотрим совокупность двух случайных величин:

Т₀ –– случайный момент отказа основного устройства;

Т₁ –– случайный момент отказа резервного устройства.

Пусть событие А –– безотказная работа технической системы до момента времени t –– состоит в том, что хотя бы одна из величин (Т₀, Т₁) примет значение, превышающее t (одно из устройств сохранит к этому моменту времени свою работоспособность). Т.е. вероятность 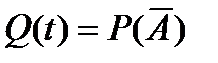того, что в момент t рассматриваемая система откажет будет соответствовать вероятности того, что случайные величины Т₀ и Т₁ примут значения меньше величины t:

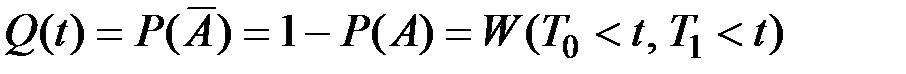(5.2)
Пусть t₀ –– фиксированный момент отказа основного устройства системы; t₁ –– фиксированный момент отказа резервного устройства.

Рис. 5.1. Общее представление характера изменения интенсивности отказов резервного устройства

Найдем совместную плотность 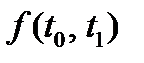распределения случайных величин Т₀ , Т₁. Поскольку эти случайные величины зависимы, то:

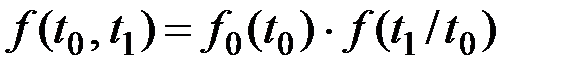(5.3)
где 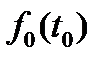–– безусловная плотность распределения случайной величины Т₀; 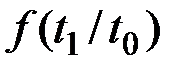–– условная плотность распределения величины Т₁ (при условии, что случайная величина Т₀ приняла значение t₀).

Как было определено ранее, плотность распределения случайного времени отказа (в общем случае) можно выразить через интенсивность отказов:

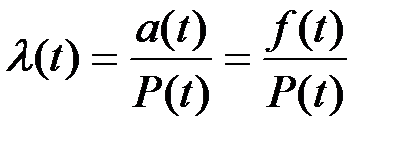
Следовательно, плотность распределения времени отказа основного устройства:

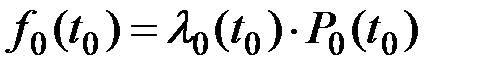(5.4)
где 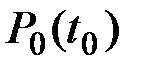–– надежность основного устройства технической системы, в общем случае равная:

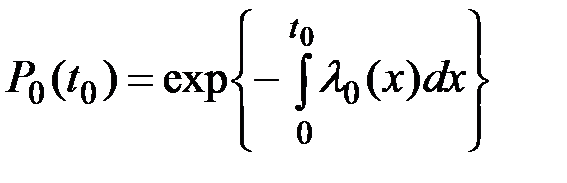(5.5)
Тогда:

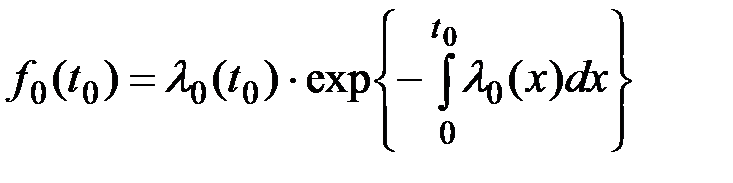(5.6)
Условная интенсивность отказов резервного устройства при условии, что случайная величина Т₀ принимает значение t₀ определяется зависимостями:

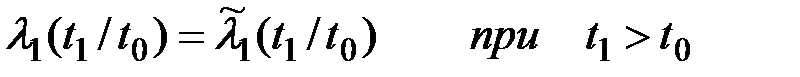
(5.7)

Вероятность безотказной работы резервного устройства при t₁< t₀ (резервное устройство отказывает раньше выхода из строя основного, не успев включиться в активный режим работы и не изменив интенсивности l₁(t) отказов) равна:

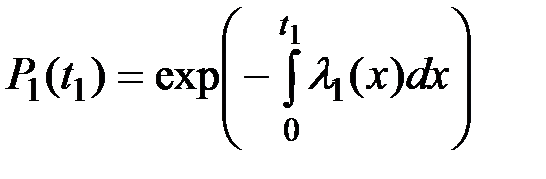
В случае отказа резервного устройства после его включения в активный режим работы (после отказа основного устройства), т.е. в случае t₁ > t₀ эта вероятность определится соотношением:

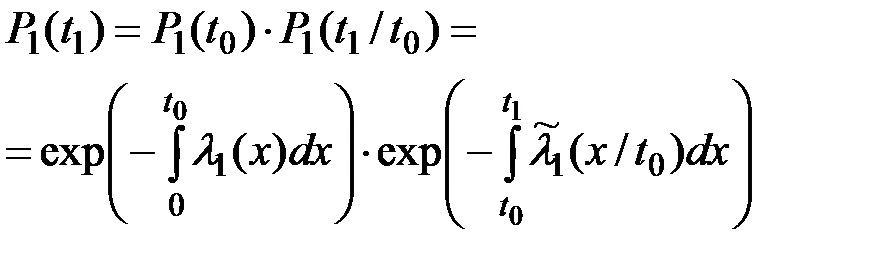
Теперь может быть определена условная плотность 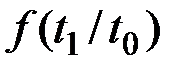распределения времени безотказной работы резервного устройства:

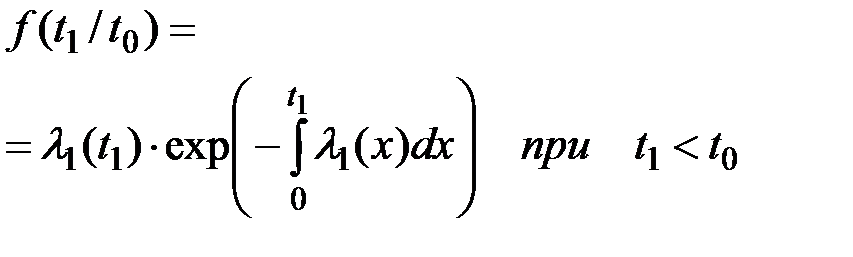(5.8)

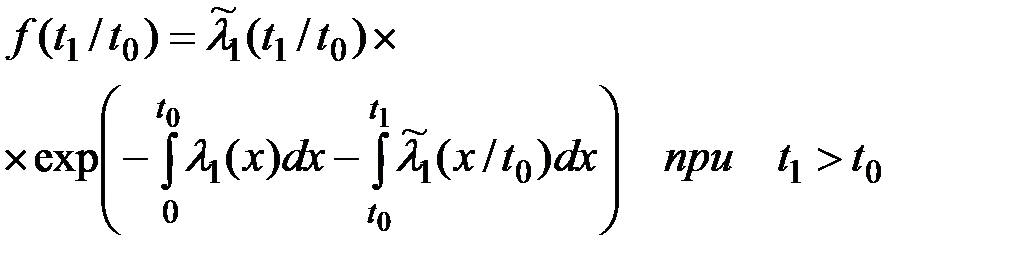(5.9)
Таким образом, совместная плотность распределения случайных величин Т₀ и Т₁ может быть определена с помощью зависимостей:

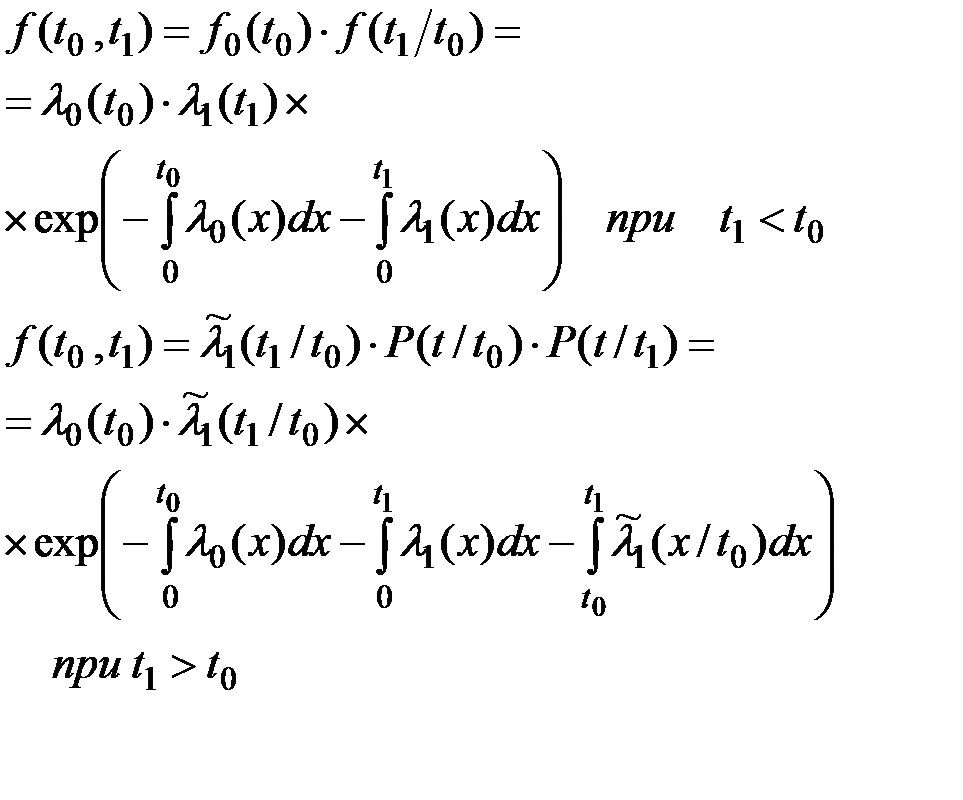(5.10)

Зная эту совместную плотность, можно найти вероятность отказа системы до интересующего момента t:

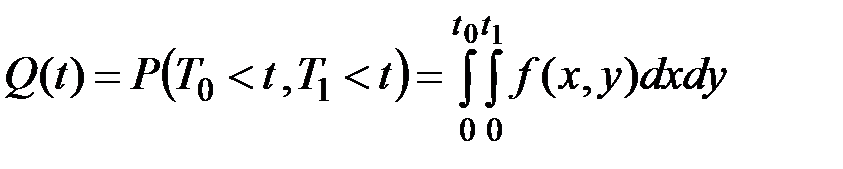(5.11)

Следовательно, надежность технической системы (вероятность ее безотказной работы в течение времени t) определится уравнением:

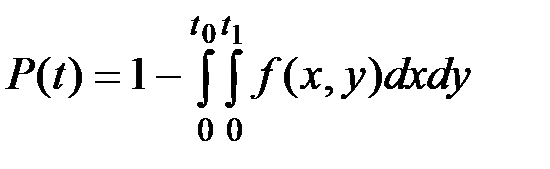(5.12)

При вычислениях по формулам (5.10), (5.11), (5.12) необходимо иметь в виду, что плотность 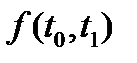имеет различные выражения по разные стороны биссектрисы первого координатного угла или прямой t₀=t₁ (рис. 5.2 ).

Рис. 5.2. Области интегрирования для вычислении надежности технической системы при нагрузочном резервировании

В области I выражение для плотности определяется первой зависимостью в формуле (5.10), т.е. при t₁<t₀. В области II –– второй зависимостью в той же формуле (при t₁>t₀). Следовательно:

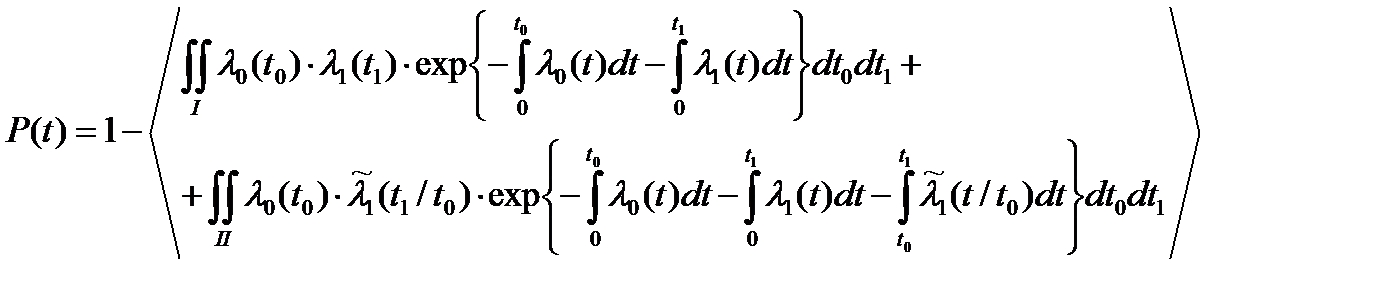(5.13)
Если вид функций l₀(t), l₁(t), 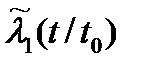известен, то интеграл (5.13) может быть вычислен, в простейших случаях аналитически, чаще – численно.

Приведенные выше рассуждения свидетельствуют о том, что даже в случае одного резервного устройства, работающего в облегченном или нагрузочном режиме, задача вычисления надежности технической системы довольно сложна. Если же число резервных устройств будет более одного, то решение усложняется весьма существенно.

Однако задача может быть значительно упрощена, если предположить, что потоки неисправностей, действующие на все устройства (основное и резервные), представляют собой простейшие потоки, интенсивность отказов каждого из которых постоянна, что равносильно тому, что закон надежности каждого устройства экспоненциальный, и включение устройства в работу меняет только параметр этого закона.

При таком допущении надежность технической системы может быть найдена путем решения системы дифференциальных уравнений для вероятностей ее состояний.

Пример 5.1.

Рассматривается система с нагрузочным резервированием и простейшим потоком отказов.

Рис. 5.3. Вид технической системы с нагрузочным резервированием, состоящей из одного основного и трех резервных устройств.

Техническая система состоит из одного основного и трех одинаковых с основным резервных устройств (рис.5.3). Основное устройство подвергается простейшему потоку отказов с интенсивностью l₀. Каждое из резервных устройств до своего включения в работу на полную нагрузку подвергается простейшему потоку отказов с интенсивностью l₁ и после включения в работу эта интенсивность для соответствующего устройства мгновенно подскакивает до значения .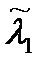

Система функционирует по алгоритму: после отказа основного устройства включается в работу устройство У₁, затем У₂ и т.д. Отказ системы адекватен отказу последнего из всех устройств. Переключающее устройство принимается идеальным.

Требуется определить надежность технической системы.

Состояние системы будем нумеровать двумя индексами. Первый индекс будем считать равным единице, если основное устройство находится в работоспособном состоянии, и равным нулю, если основное устройство отказало. Второй индекс будем принимать равным числу исправных резервных устройств. Тогда состояния системы принимают следующие обозначения:

S₁₃ –– в исправном состоянии находятся все четыре устройства технической системы (основное и три резервных);S₁₂ –– исправно основное устройство, из трех резервных устройств одно отказало, два находятся в исправном состоянии;S₁₁ –– основное устройство исправно и исправно одно резервное;S₁₀ –– исправно только основное устройство, все три резервных отказали;S₀₃ –– основное устройство отказало, все три резервных исправны;S₀₂ –– основное устройство отказало, исправны два резервных устройства;S₀₁ –– основное устройство отказало, работает только одно из резервных;

S₀₀ –– отказали все четыре устройства (произошел отказ системы).

₁

Рис. 5.4. Размеченный граф состояний технической системы с «нагруженным» резервированием

Система уравнений Колмогорова для вероятностей состояний рассматриваемой системы имеет вид:

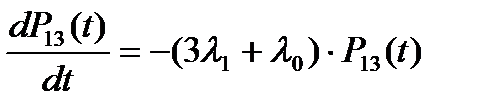
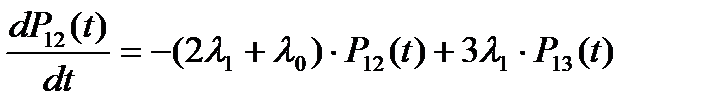
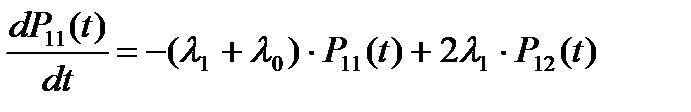
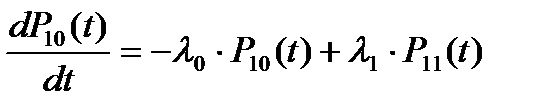
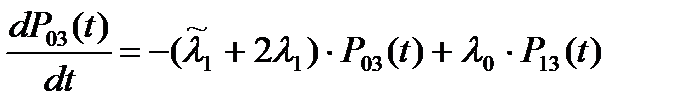(5.14)

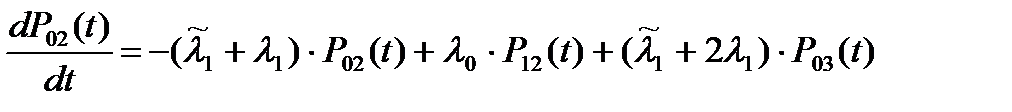
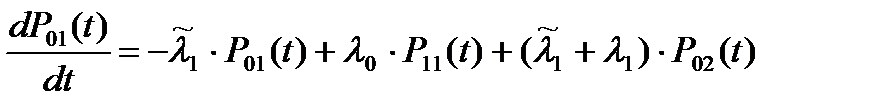
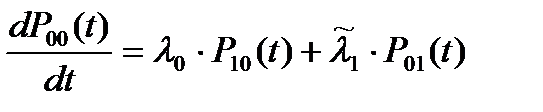
К этим уравнениям необходимо добавить условие:

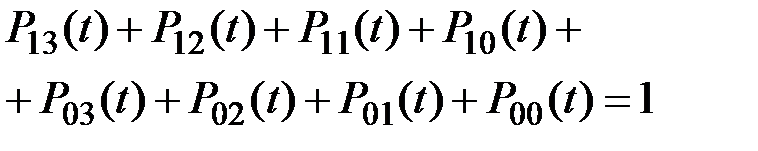(5.15)
которое позволяет исключить одно (любое) из уравнений Колмогорова.

Интегрирование системы уравнений (5.14) может быть осуществлено в следующей последовательности: из первого уравнения находится функция P₁₃(t), равная

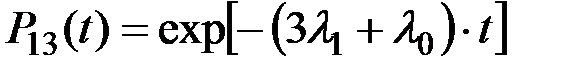(5.16)
Это выражение подставляется во второе уравнение, которое теперь содержит только одну неизвестную функцию P₁₂(t), которую достаточно легко можно определить и подставить в третье уравнение, и т.д. На каждом шаге такого процесса новые выражения функций мы находим через уже известные, пока не доходим до функции P₀₀(t), которую выражаем через все остальные:

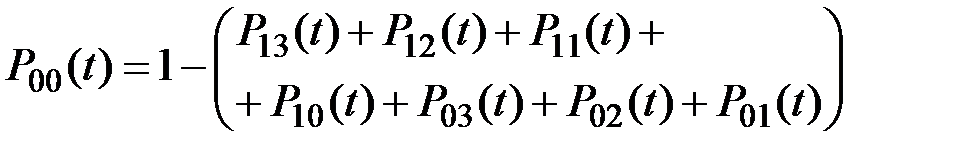(5.17)
Теперь можно определить надежность P(t) рассматриваемой технической системы:

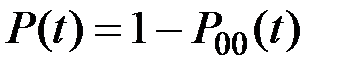(5.18)

Пример изменения вероятностей нахождения системы в перечисленных выше состояниях, рассчитанных с помощью Mathсad, приведен на рис. 5.5.

Рис. 5.5 Изменение вероятностей состояния системы.

На рис. 5.5 введены обозначения:

P₁₃=Р_t,1, P₁₂=P_t,2, P₁₁=P_t,3, P₁₀=P_t,4, P₀₃=P_t,5, P₀₂=P_t,6, P₀₁=P_t,7, P₀₀=P_t,8.

n - число шагов интегрирования в функции rkfixed пакета Mathcad.

Расчеты проводились при l₁=5 ¹/_год, l₀=20 ¹/_год, 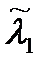=10 ¹/_год , n=100.

Несколько упростим задачу и примем следующие допущения:

отказы всех устройств технической системы представляют собой простейшие потоки случайных событий;

переключающие элементы абсолютно надежны и срабатывают мгновенно.

Первое допущение означает, что интенсивности отказов устройств не изменяются во времени и их распределение подчинено экспоненциальному закону. Кроме того, в силу идентичности устройств, интенсивности отказов устройств, находящихся в резервном режиме работы, равны между собой.

Пусть t₀ –– момент отказа основного устройства технической системы или резервного устройства, работавшего с полной нагрузкой. Обозначим через l_А интенсивность отказов устройства, работающего в активном (с полной нагрузкой) режиме, а через l_Р –– интенсивность отказов устройства, находящегося в резерве (в облегченном режиме нагружения). Изменение интенсивности отказов любого из резервных устройств происходит скачкообразно в момент перехода устройства в активный режим работы (рис.5.5).

Рис.5.6. Изменение интенсивности отказов резервных устройств.

Основное устройство технической системы имеет с момента включения технической системы интенсивность отказов, равную l_А.

Вывод основных показателей надежности технической системы, резервированной по принципу «теплого» резервирования, базируется на следующих рекуррентных соотношениях:

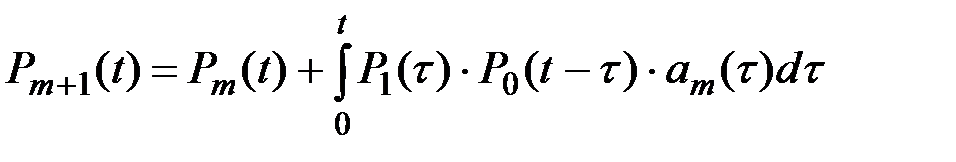(5.19)
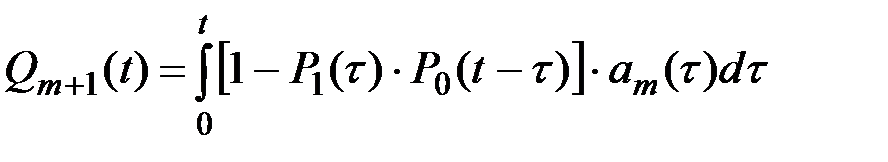(5.20)
где Р₁(t) –– вероятность безотказной работы резервного устройства до момента его включения в активную (полную) нагрузку; Р₀(t-t) –– вероятность безотказной работы резервного устройства от момента t включения его в работу до момента времени t; a_m(t) –– частота отказов резервного устройства после его включения в активный режим работы.

Опуская промежуточные выкладки, приведем окончательные выражения для вероятности безотказной работы технической системы при различной кратности резервирования в режиме «облегченного» резерва.

При m=1 (одно резервное устройство, т.е. всего в системе 2 устройства):

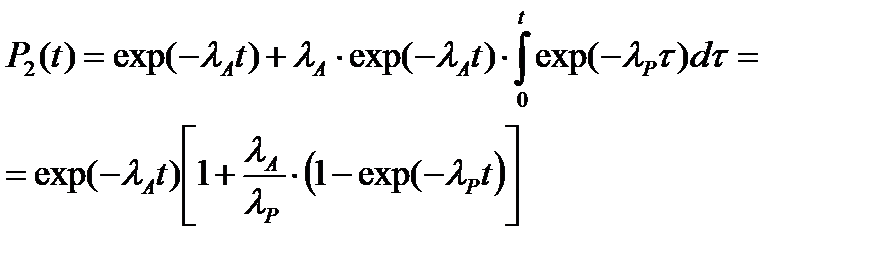(5.21)
При m=2 (два резервных устройства и одно основное):

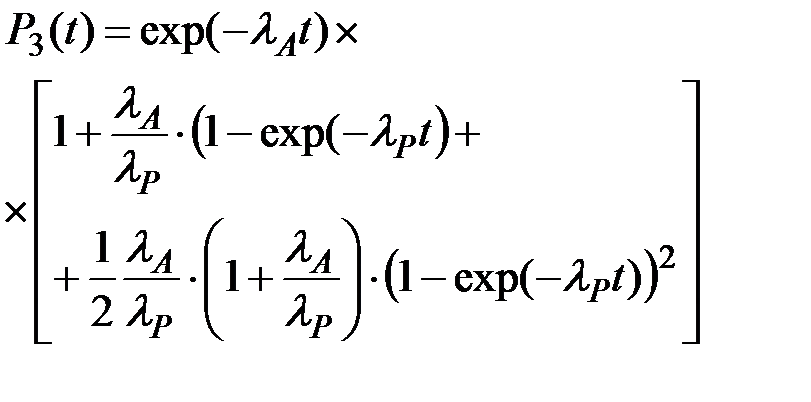(5.22)
Анализ представленных зависимостей и их аналогов для m=3 дает основание для установления закономерности, позволяющей записать выражение для вероятности безотказной работы P_C(t) технической системы при произвольной кратности резервирования (общее число устройств равно m+1):

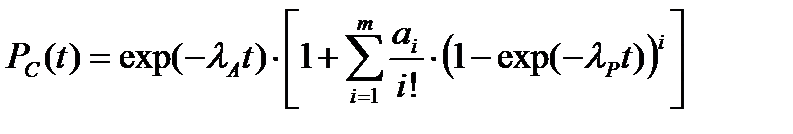(5.23)

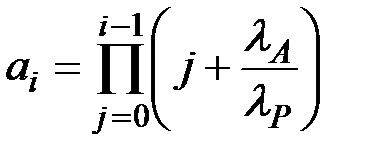(5.24)
Из выражения (5.23) видно, что вероятность безотказной работы m-кратно резервированной технической системы может быть вычислена так же с помощью рекуррентного соотношения:

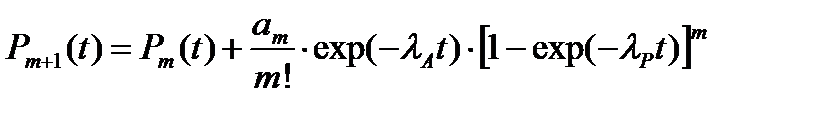(5.25)

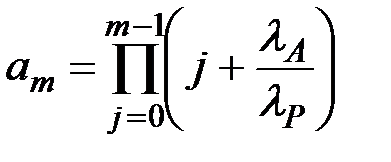(5.26)

Интегрирование (5.25) позволяет найти выражение для расчета среднего времени Т_С безотказной работы технической системы:

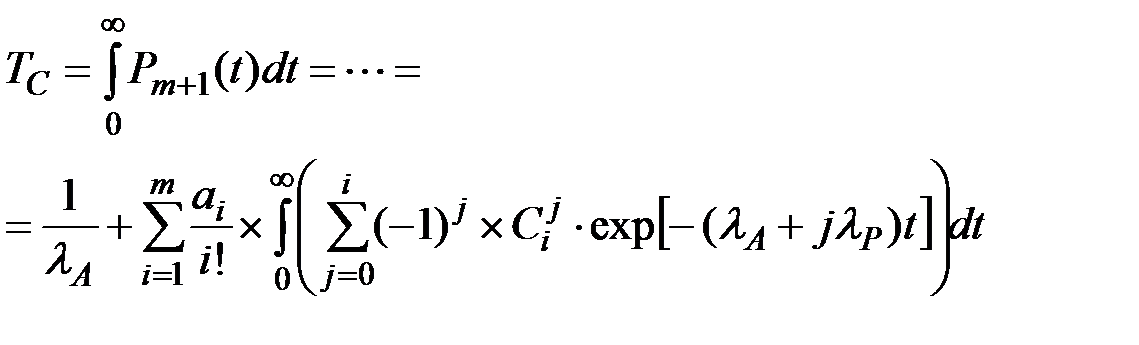(5.27)
В окончательном виде после интегрирования (5.27):

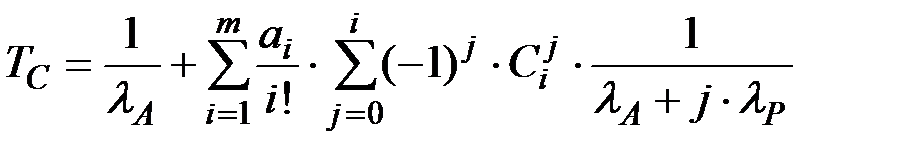(5.28)
Частота отказов системы:

(5.29)

Рис. 5.7. Изменение вероятности безотказной работы системы

Интенсивность отказов технической системы:

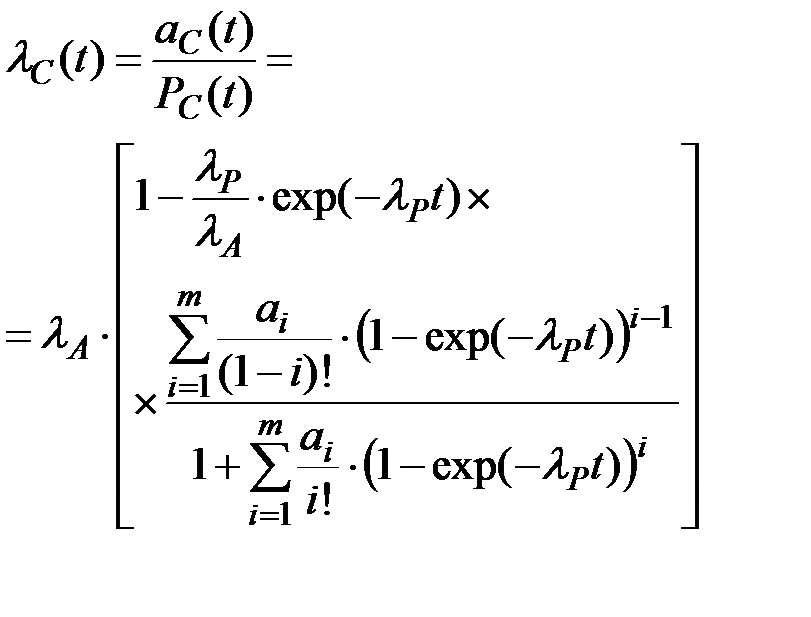(5.30)
Изменение надежности системы при различном числе m резервных устройств и при значениях интенсивностей отказов l_А =10^-3 1/час, l_Р =10^-4 1/час приведено на рис.5.7.

Изменение частоты отказов технической системы с теми же параметрами представлено на рис.5.8.

Рис.5.8. Изменение частоты отказов а_с×10^-4 технической системы, рассчитанной по формуле (5.29) при l_А=0.001 1/час, l_Р=0.0001 1/час

На рис.5.9 приведены графики изменения интенсивности отказов технической системы в тех же условиях.

Рис.5.9. Изменение интенсивности отказов l_С×10^-4 (1/час) технической системы, рассчитанной по формуле (5.30) при исходных данных, совпадающих с данными рис. 5.8

Анализ кривых, представленных на рис. 5.8, рис. 5.9 показывает, что локальное снижение интенсивности и частоты отказов объясняется достаточным количеством резервных устройств, находящихся в исправном состоянии. Снижение частоты отказов на конечном этапе эксплуатации системы объясняется уменьшением общего числа работоспособных устройств.