Расчетно-графическая работа № 3.1.
Исследование надежности нерезервированной технической системы в период нормальной эксплуатации (без учета старения элементов).
Основными показателями надежности нерезервированных невосстанавливаемых систем являются:
Pc(t) –– вероятность безотказной работы системы в течение времени t;
TС –– среднее время безотказной работы системы.
При постоянных значениях (неизменяемых во времени) интенсивностей отказов элементов, имеем:
,
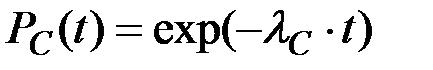
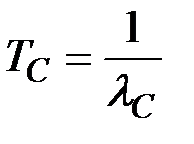где lС –– интенсивность отказов системы, li - интенсивность элемента.
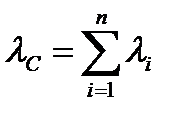
Исходные данные для выполнения лабораторной работы:
число элементов системы n=10; время Т непрерывной работы системы; интенсивности li отказов каждого элемента (табл. 3.1).
Требуется:
определить интенсивность отказов системы; определить ожидаемое время безотказной работы системы; построить функцию изменения вероятности безотказной работы системы; вычислить вероятность нахождения системы в рабочем состоянии в течение времени ее непрерывной работы; определить верхнюю и нижнюю границы вероятности безотказной работы системы в течение времени ее непрерывной работы.
Значения интенсивностей отказов элементов li×10-5 1/час и времени непрерывной работы (час) для выполнения расчетной работы № 3.1.
Таблица 3.1
| Вар-нт Эл-т | ||||||||||||||
| i=1 | 2.4 | 0.3 | 5.5 | 0.4 | 3.5 | 0.7 | 0.7 | 3.1 | 4.4 | 1.0 | 4.3 | 0.5 | 7.1 | 1.8 |
| i=2 | 1.7 | 0.7 | 4.8 | 0.5 | 4.8 | 0.5 | 0.4 | 2.0 | 2.0 | 1.4 | 4.2 | 0.1 | 7.2 | 1.4 |
| i=3 | 3.3 | 1.1 | 3.9 | 0.9 | 8.7 | 0.4 | 9.3 | 1.5 | 2.4 | 1.2 | 3.6 | 0.4 | 7.0 | 1.9 |
| i=4 | 0.8 | 0.2 | 2.7 | 0.5 | 5.5 | 1.9 | 4.2 | 2.2 | 2.6 | 1.6 | 2.8 | 6.6 | 6.5 | 1.2 |
| i=5 | 0.3 | 0.8 | 8.1 | 0.3 | 4.9 | 1.7 | 5.3 | 0.3 | 2.5 | 1.8 | 9.1 | 3.1 | 3.3 | 1.1 |
| i=6 | 1.4 | 0.4 | 0.5 | 0.2 | 6.6 | 0.7 | 1.1 | 0.4 | 2.1 | 1.9 | 1.0 | 0.2 | 4.3 | 0.3 |
| i=7 | 2.6 | 1.5 | 0.3 | 0.7 | 6.9 | 6.1 | 1.5 | 2.6 | 2.0 | 1.4 | 0.2 | 0.1 | 0.1 | 0.2 |
| i=8 | 5.1 | 1.2 | 4.6 | 0.4 | 4.2 | 1.2 | 3.2 | 1.1 | 2.3 | 1.2 | 0.1 | 0.7 | 0.2 | 4.0 |
| i=9 | 2.9 | 2.0 | 5.3 | 1.3 | 8.7 | 0.1 | 2.7 | 1.7 | 0.1 | 1.1 | 0.3 | 4.5 | 3.3 | 1.1 |
| i=10 | 1.3 | 0.9 | 3.3 | 1.0 | 9.1 | 0.3 | 2.2 | 1.0 | 0.1 | 1.9 | 2.2 | 4.3 | 2.8 | 0.5 |
| Т×1000 | 2.9 | 1.2 | 2.3 | 2.5 | 2.1 | 2.2 | 1.7 | 2.0 | 1.8 | 2.1 | 1.9 | 2.7 | 1.7 | 1.4 |
Продолжение таблицы 3.1.
| Вар-нт Эл-т | ||||||||||||||
| i=1 | 1.4 | 0.5 | 5.6 | 1.4 | 3.5 | 6.7 | 1.7 | 3.5 | 4.7 | 1.7 | 4.2 | 8.5 | 7.5 | 1.9 |
| i=2 | 3.7 | 0.8 | 5.8 | 0.6 | 4.8 | 0.7 | 2.4 | 2.1 | 2.9 | 1.8 | 4.7 | 3.1 | 7.3 | 4.4 |
| i=3 | 3.2 | 2.1 | 2.9 | 1.9 | 8.7 | 1.4 | 3.3 | 2.5 | 2.6 | 1.4 | 3.1 | 1.4 | 7.4 | 7.9 |
| i=4 | 1.8 | 0.5 | 2.9 | 0.9 | 5.5 | 2.9 | 4.2 | 1.2 | 2.3 | 1.6 | 2.8 | 6.7 | 6.5 | 1.4 |
| i=5 | 0.9 | 0.7 | 8.3 | 4.3 | 4.9 | 1.8 | 5.3 | 5.3 | 2.6 | 1.9 | 9.5 | 3.2 | 3.6 | 3.1 |
| i=6 | 1.7 | 1.4 | 1.5 | 0.2 | 3.7 | 0.6 | 6.1 | 6.4 | 2.2 | 1.3 | 1.9 | 5.2 | 4.3 | 6.3 |
| i=7 | 2.5 | 2.5 | 2.3 | 0.7 | 6.6 | 5.1 | 7.5 | 2.6 | 2.7 | 8.4 | 6.2 | 0.4 | 8.1 | 6.2 |
| i=8 | 4.1 | 1.7 | 5.6 | 0.4 | 4.8 | 8.2 | 2.2 | 1.3 | 1.3 | 5.2 | 3.1 | 2.7 | 4.2 | 8.0 |
| i=9 | 2.5 | 2.7 | 6.3 | 1.3 | 6.7 | 1.1 | 5.7 | 1.4 | 1.1 | 3.1 | 8.3 | 4.8 | 8.3 | 3.1 |
| i=10 | 1.7 | 0.5 | 4.3 | 1.0 | 7.1 | 2.3 | 2.4 | 1.6 | 6.1 | 6.9 | 7.2 | 6.3 | 3.8 | 4.5 |
| Т×1000 | 1.3 | 2.2 | 3.3 | 2.5 | 2.7 | 3.2 | 2.7 | 2.4 | 1.7 | 6.1 | 7.0 | 2.2 | 2.1 | 3.0 |
Пример 3.1.Расчет изменения во времени верхней и нижней границ надежности технической системы в среде Matlab [9, 10].
n=10;t=0:1000;
k=unifrnd(1,10,1,n);L=k*10^-4;LM=max(L);LS=sum(L);
PM=exp(-LM.*t);P=exp(-LS.*t);Pm=exp(-n*LM.*t);
plot(t,PM,'k+',t,P,'k+',t,Pm,'ko')
grid on
xlabel('t')
ylabel('nadegnoct')
Рис.3.1. Изменение надежности P(t), верхней границы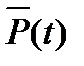 
=PM и нижней границы 
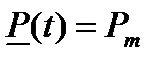нерезервированной системы с учетом только внезапных отказов
Дата добавления: 2019-02-07; просмотров: 304;