Надежность технических систем и техногенный риск.
Надежность технической системы – это вероятность сохранения системой работоспособности в течение определенного времени.
Техническую систему будем представлять в виде сложной системы следующей иерархии:
- техническая система;
- устройства;
- элементы.
Техническая система –– совокупность взаимосвязанных элементов (объектов, устройств), обеспечивающих выполнение конкретных практических задач.
Устройством называется законченная конструкция, которая, являясь частью системы, имеет самостоятельное целевое назначение.
Элементы –– это части системы или устройства, которые выполняют в нем определенные функции и не могут иметь самостоятельного (вне связи с другими элементами или устройствами) применение.
Причины недостаточной надежности технических систем.
Основными причинами отказов технических систем являются внезапные (случайные) отказы, отказы вследствие ухудшения характеристик элементов (старение, износ), а также по вине скрытых производственных дефектов, характерных для начального периода эксплуатации, или нарушения условий эксплуатации [3].
Возрастание интенсивности отказов технических систем связано, как правило, с ужесточением условий их функционирования (эксплуатации) и с недостаточной квалификацией обслуживающего персонала.
В целом, все причины, приводящие к снижению надежности технических систем, можно разделить на следующие: конструктивные, производственные, эксплуатационные, организационные.
Конструктивные причины: низкая надежность элементной базы, неправильный выбор элементов, неудачное схемно-компоновочное решение, недостаточная унификация элементов, недостаточная отработка технологий на этапах испытаний.
Производственные причины: нарушение качества материалов, недостаточный контроль входных параметров, недостаточная отработка технологии производства и сборки устройств, общая низкая культура производства.
Эксплуатационные причины: низкая квалификация технического персонала, низкая эффективность контрольно––проверочной аппаратуры, нарушение условий эксплуатации.
Организационные причины: отсутствие требований по поддержанию заданных показателей надежности, несоответствие заводских испытаний реальным условиям эксплуатации, неритмичность эксплуатации.
1.3. Цена надежности.
Стоимость технической системы, как правило, определяется стоимостью ее создания (строительства) и стоимостью эксплуатации системы и зависит от надежности системы.
Cå (Р)= C0 (Р) + Cэ (Р)
где Cå (Р) –– общая стоимость технической системы;
C0(Р) –– стоимость создания технической системы;
Cэ(Р) –– стоимость эксплуатации технической системы,
Р –– надежность системы.
Расходы, связанные с созданием технической системы, являются функцией требований к ее надежности. Чем выше требования к надежности системы, тем выше ее стоимость, т.е. функция C0 (P) –– неубывающая функция надежности системы (рис. 1.2).
Стоимость эксплуатации технической системы также зависит от ее надежности, но в обратной зависимости. Чем выше надежность системы, тем ниже стоимость ее эксплуатации, чем надежнее создана система, тем меньше средств она требует на свое поддержание в исправном состоянии.
Рис. 1.2. Изменение суммарной стоимости СS системы в зависимости от ее надежности Р, затрат на эксплуатацию СЭ и создание системы С0.
Рациональное распределение средств на повышение надежности технических систем на этапе проектирования, изготовления, испытания и эксплуатации может привести к существенной экономии суммарных расходов обеспечения функционирования системы. Зачастую распределение средств, выделенных на снижение негативных последствий аварий принимается за управление риском.
Анализ опасностей и оценки риска аварий на опасных производственных объектах (далее - анализ риска аварий) представляют собой совокупность научно-технических методов исследования опасностей возникновения, развития и последствий возможных аварий, включающую планирование работ, идентификацию опасностей аварий, оценку риска аварий, установление степени опасности возможных аварий, а также разработку и своевременную корректировку мероприятий по снижению риска аварий [4].
Риск аварии [5] - мера опасности, характеризующая возможность возникновения аварии на опасном производственном объекте и соответствующую ей тяжесть последствий. В анализе риска аварий в качестве основных количественных показателей опасности (показателей риска) рекомендуется использовать:
технический риск - вероятность отказа технических устройств с последствиями определенного уровня (класса) за определенный период функционирования опасного производственного объекта;
индивидуальный риск - ожидаемая частота (частота) поражения отдельного человека в результате воздействия исследуемых поражающих факторов аварии;
потенциальный территориальный риск (или потенциальный риск)– частота реализации поражающих факторов аварии в рассматриваемой точке на площадке опасного производственного объекта и прилегающей территории;
коллективный риск (или ожидаемые людские потери) - ожидаемое
количество пораженных в результате возможных аварий за определенный период времени;
социальный риск (или риск поражения группы людей) - зависимость частоты возникновения сценариев аварий F, в которых пострадало на определенном уровне не менее N человек, от этого числа N. Характеризует социальную тяжесть последствий (катастрофичность) реализации совокупности сценариев аварии и представляется в виде соответствующей F/N-кривой;
ожидаемый ущерб - математическое ожидание величины ущерба от возможной аварии за определенный период времени;
материальный риск (или риск материальных потерь) - зависимость частоты возникновения сценариев аварий F, в которых причинен ущерб на определенном уровне потерь не менее G, от количества этих потерь G. Характеризует экономическую тяжесть последствий реализации опасностей аварий и представляется в виде соответствующей F/G-кривой.
Для некоторых ситуаций определены допустимые значения риска, например, [6] нормативные значения пожарного риска для производственных объектов.
Величина индивидуального пожарного риска в зданиях, сооружениях, строениях и на территориях производственных объектов не должна превышать одну миллионную в год.
Риск гибели людей в результате воздействия опасных факторов пожара должен определяться с учетом функционирования систем обеспечения пожарной безопасности зданий, сооружений и строений.
Для производственных объектов, на которых обеспечение величины индивидуального пожарного риска одной миллионной в год невозможно в связи со спецификой функционирования технологических процессов, допускается увеличение индивидуального пожарного риска до одной десятитысячной в год. При этом должны быть предусмотрены меры по обучению персонала действиям при пожаре и по социальной защите работников, компенсирующие их работу в условиях повышенного риска.
Величина индивидуального пожарного риска в результате воздействия опасных факторов пожара на производственном объекте для людей, находящихся в селитебной зоне вблизи объекта, не должна превышать одну стомиллионную в год.
Величина социального пожарного риска воздействия опасных факторов пожара на производственном объекте для людей, находящихся в селитебной зоне вблизи объекта, не должна превышать одну десятимиллионную в год.
Наиболее распространенной методикой количественной оценки риска является мультипликативная форма его представления [7]:
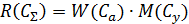
где: 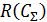 - значение риска;
- значение риска;
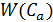 – вероятность возникновения хотя бы одной аварии за рассматриваемый период работы объекта или технической системы;
– вероятность возникновения хотя бы одной аварии за рассматриваемый период работы объекта или технической системы;
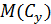 - ожидаемый ущерб при возникновении аварии;
- ожидаемый ущерб при возникновении аварии;
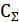 – средства, выделяемые на снижение риска;
– средства, выделяемые на снижение риска;
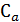 – средства, выделяемые на снижение вероятности реализации аварии;
– средства, выделяемые на снижение вероятности реализации аварии;
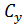 – средства, выделяемые на снижение ожидаемого ущерба в случае возникновения аварии.
– средства, выделяемые на снижение ожидаемого ущерба в случае возникновения аварии.
Основной принцип управления риском состоит в приоритетном максимальном снижении вероятности возникновения аварии, и во вторую очередь – забота о сокращении ожидаемого ущерба.
Возникновение аварии очевидным образом непосредственно связано с надежностью технических систем, ее устройств или элементов.
Следует заметить, что вероятность возникновения хотя бы одной аварии имеет существенное отличие от вероятности возникновения ровно одной аварии.
2. Основные понятия теории надежности.
Теория надежности в большинстве случаев оперирует случайными величинами, поэтому большая часть понятий и определений связана с понятийным аппаратом теории вероятностей.
Отказ –– полная или частичная утрата работоспособности элементом, устройством или рассматриваемой технической системой.
Исправность –– состояние системы, при котором она в данный момент времени соответствует всем требованиям, установленным в отношении как основных параметров, так и «второстепенных».
Работоспособность –– состояние системы, при котором она в данный момент времени соответствует всем требованиям, установленным в отношении ее основных параметров.
Безотказность –– свойство системы сохранять работоспособность в течение заданного интервала времени в определенных условиях эксплуатации.
Неисправность –– состояние системы, при котором она в данный момент времени не соответствует хотя бы одному из требований, установленных в отношении как основных параметров, так и «второстепенных».
2.1. Основные количественные характеристики надежности и связь между ними.
Основной количественной характеристикой надежности является вероятность безотказной работы, определяемая как вероятность P(t) нахождения системы в исправном состоянии в течение времени T ³ t, где Т –– случайная величина продолжительности работы системы до отказа, t –– детерминированная величина текущего времени или его конкретное значение [8]:
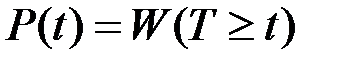 (2.1)
(2.1)
где W(T) –– вероятность реализации события, заключающегося в том, что отказ системы не произойдет ранее t.
Функция P(t) обладает следующими свойствами:
P(0) = 1, P(¥) = 0, P(t2) £ P(t1) при t2 > t1,
т.е. функция P(t) –– невозрастающая функция времени.
Эту функцию часто называют функцией надежности или просто надежностью технической системы.
Характеристикой, противоположной надежности, является вероятность отказа Q(t), как вероятность того, что устройство или техническая система откажет в течение времени T < t :
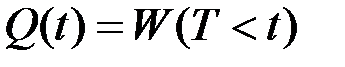 (2.2)
(2.2)
Свойства функции Q(t) : Q(0) = 0, Q(¥) = 1, Q(t2) ³ Q(t1) при t2 > t1 .
Таким образом, функция ненадежности Q(t) представляет собой функцию распределения времени исправной работы системы F(t) (П 2.20) Приложения 2.
Очевидно: Q(t) + P(t) = 1; Q(t)=1-P(t);
| t |
| Q(t) |
| P(t) |
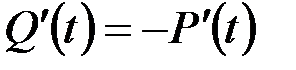 (2.3)
(2.3)т.е. система может находиться либо в исправном, либо в неисправном состоянии.
Рис. 2.1. Характер изменения функций надежности и отказов во времени.
Плотность f(t) распределения времени работы системы до отказа согласно определению плотности из классической теории вероятностей имеет вид (П 2.21) приложения 2:
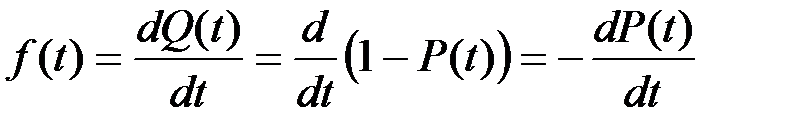 (2.4)
(2.4)
Наряду с аналитическими методами определения различных параметров надежности широко используются статистические методы, с помощью которых определяются так называемые статистические характеристики надежности систем. Эти характеристики представляют собой результаты обработки экспериментальных данных или данных прямых наблюдений.
Поскольку в эксперименте невозможно произвести наблюдения при t®¥ или на бесконечно малом временном интервале Dt®0, а также при бесконечно большом числе испытываемых систем, то статистические характеристики следует рассматривать как оценочные или приближенные к теоретическим. Статистическая плотность отказов 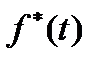 в теории надежности определяют в виде отношения:
в теории надежности определяют в виде отношения:
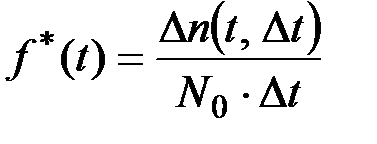 (2.5)
(2.5)
где Dn(t, Dt) –– число отказавших элементов на интервале Dt (от момента времени t до момента t+Dt); N0 –– общее число элементов, выставленных на испытания; Dt ––интервал времени проведения испытаний или наблюдений.
| n(t,∆t)-n(t)=∆n |
| Вышедшие из строя |
| n(t) |
| t |
| n(t,∆t) |
| t+∆t |
| T |
Рис. 2.2. Порядок вычисления количества отказавших элементов Dn.
Статистически функция распределения времени исправной работы Q*(t) системы оценивается как отношение числа устройств n(t), вышедших из строя за время от начала испытаний до некоторого момента t, к общему числу элементов или устройств N0, поставленных на испытание:
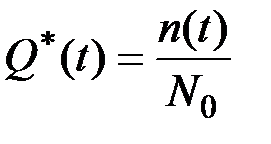 (2.6)
(2.6)
Величину Q*(t) называют частостью отказов, которая является оценкой функции распределения отказов или вероятности отказа.
Очевидно, что чем больше проведено число независимых испытаний, тем ближе величина частости к соответствующему значению вероятности. В теории вероятностей такой характер приближения одних величин к другим чрезвычайно употребителен и для его описания введен специальный термин –– сходимость по вероятности.
Согласно первой предельной теореме (закон больших чисел), последовательность случайных величин xn сходится по вероятности к величине J, если при сколь угодно малом e>0 вероятность неравенства
½xn - J½< e с увеличением n неограниченно приближается к единице.
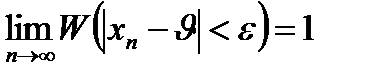
Таким образом, можно утверждать, что с увеличением числа опытов частость события сходится к его вероятности по вероятности.
Одной из характеристик надежности технических систем является частота отказов, в дальнейшем обозначаемая a(t).
Частотой отказов а*(t) называется отношение числа отказавших образцов в единицу времени к числу образцов, первоначально установленных на испытание при условии, что отказавшие образцы не восстанавливаются и не заменяются исправными.
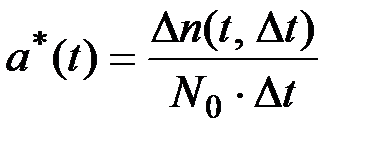 (2.7)
(2.7)
Выражение (2.9) является статистическим определением частоты отказов. Вместе с тем этой характеристике можно придать вероятностное определение.
Число отказавших образцов на интервале Dt может быть определено по формуле:
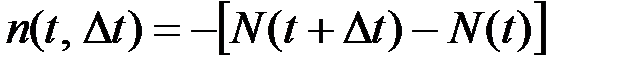 (2.8)
(2.8)
где N(t) –– число образцов, исправно работающих к моменту t; N(t+Dt) –– число образцов, исправно работающих к моменту t+Dt.
При достаточно большом числе образцов N0 справедливы следующие соотношения:
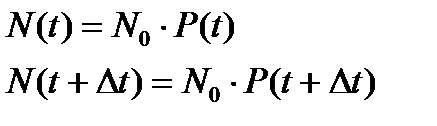 (2.9)
(2.9)
где P(t)- вероятность сохранения работоспособности исследуемым элементом до момента t, т.е. надежность рассматриваемого элемента.
Подставляя (2.8) в (2.9) и учитывая (2.7), получим:
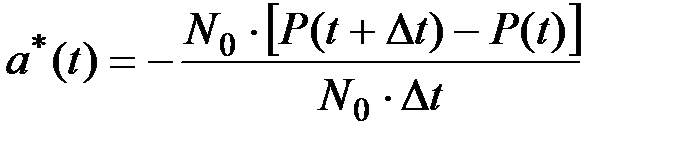 (2.10)
(2.10)
Устремляя к нулевому пределу интервал Dt, получим с учетом определения Dn(t, Dt), принятого в (2.5):
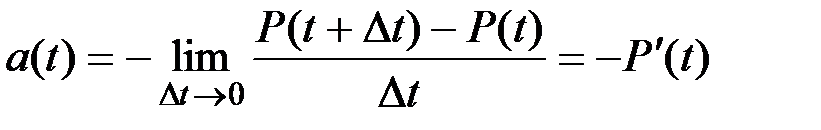 (2.11)
(2.11)
или
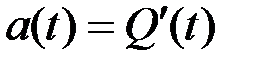
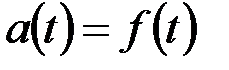 (2.12)
(2.12)
Последнее равенство подтверждает идентичность (2.7), (2.10).
Из выражения (2.12) следует утверждение, что частота отказов представляет собой плотность распределения времени работы системы до ее отказа.
Наиболее употребительной в теории надежности является такая характеристика, как интенсивность отказов:
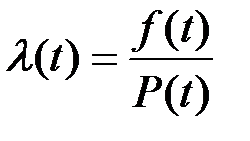 (2.13)
(2.13)
т.е. l(t) является условной плотностью распределения вероятности исправной работы системы, вычисленной при условии, что к моменту t система была исправна.
Статистической интерпретацией интенсивности отказов l(t)* является отношение числа однотипных устройств Dn(Dt) , вышедших из строя в интервале времени Dt , к числу устройств N(t) из общего числа N0 , поставленных на испытания, продолжающих к моменту времени t оставаться исправными, умноженному на длину интервала Dt, при условии, что отказавшие образцы не восстанавливаются и не заменяются исправными.
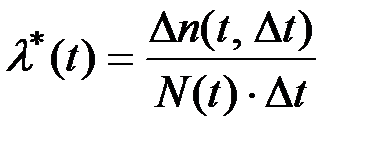 (2.14)
(2.14)
Разделив числитель и знаменатель (2.14) на N0, получим:
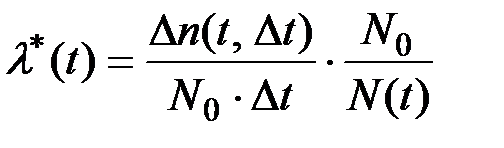 ,
,
или
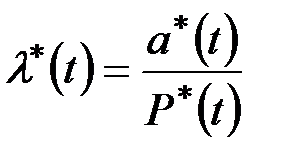 (2.15)
(2.15)
Таким образом, интенсивность отказов определяется как отношение частоты отказов к статистической оценке вероятности P(t) исправной работы рассматриваемого элемента или устройства
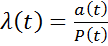 (2.16)
(2.16)
P(t)= 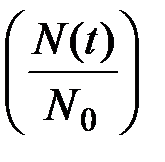 (2.17)
(2.17)
Типичная кривая изменения интенсивности отказов технических систем представлена на рисунке 2.3.
| l(t) |
| t2 |
| t |
Рис. 2.3. Типовая зависимость интенсивности отказов технических систем от времени.
Как видно из рис. 2.3 кривая l(t) имеет три характерных участка. Первый участок (от 0 до t1) –– участок приработки, второй участок (от t1 до t2) –– участок нормальной эксплуатации системы, третий временной интервал (от t2 и далее) –– участок старения системы. Здесь уместно отметить, что в период нормальной работы системы (от t1 до t2), как правило, интенсивность отказов не зависит от времени, l=const.
Выражение (2.16) с учетом (2.11) приобретает вид:
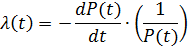
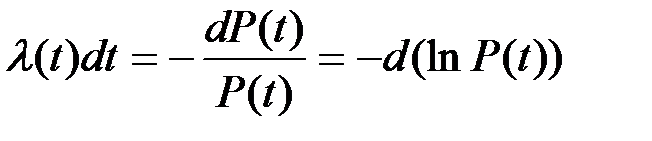 (2.18)
(2.18)
Интегрируя (2.18) при начальном условии P(0) = 1, получим:
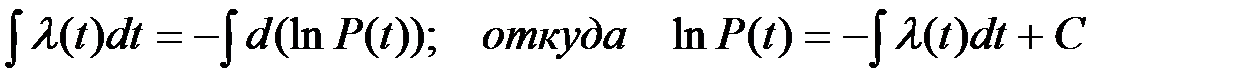
или
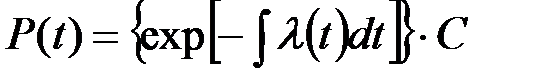
Поскольку 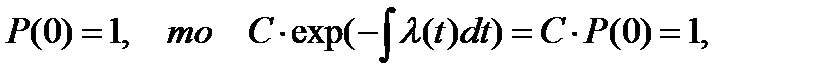 т.е. С=1.
т.е. С=1.
Нижний предел интегрирования равен 0, т.к. отсчет времени производится от момента включения системы в работу.
Верхний предел определяется аргументом функции P(t) т.е. значением аргумента t.
Окончательно получаем:
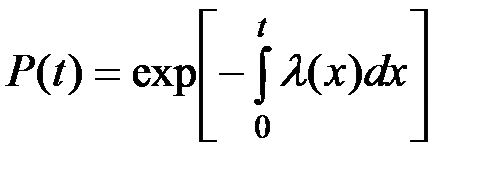 (2.19)
(2.19)
Выражение (2.19) определяет вероятность безотказной работы технических систем и является одним из основных в теории надежности.
Среднее время до отказа технической системы ТС определяется как его математическое ожидание с нижним пределом интегрирования, равным нулю, поскольку время не имеет отрицательных значений:
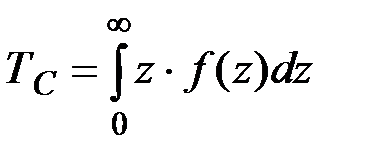 (2.20)
(2.20)
Статистической интерпретацией среднего времени до первого отказа является среднее арифметическое значение времени работы устройства до ее первого отказа:
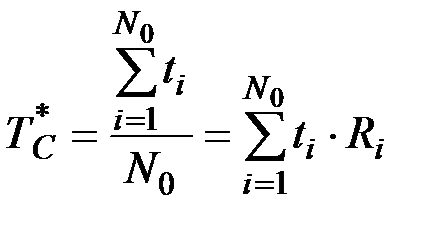 (2.21)
(2.21)
где Ri –– называют частостью времени отказов ti; ti –– время работы i-го элемента до первого отказа; N0 –– число элементов, поставленных на испытание.
Выражение (2.20) можно представить в ином виде, подставив выражение плотности f(t) согласно (2.4):
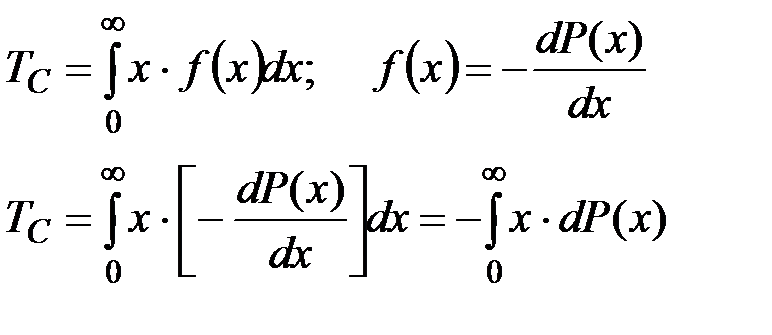 (2.22)
(2.22)
Произведем интегрирование по частям:
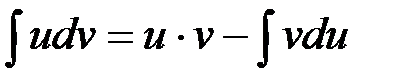
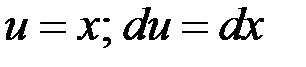
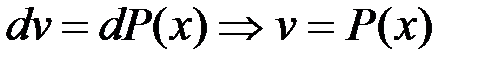
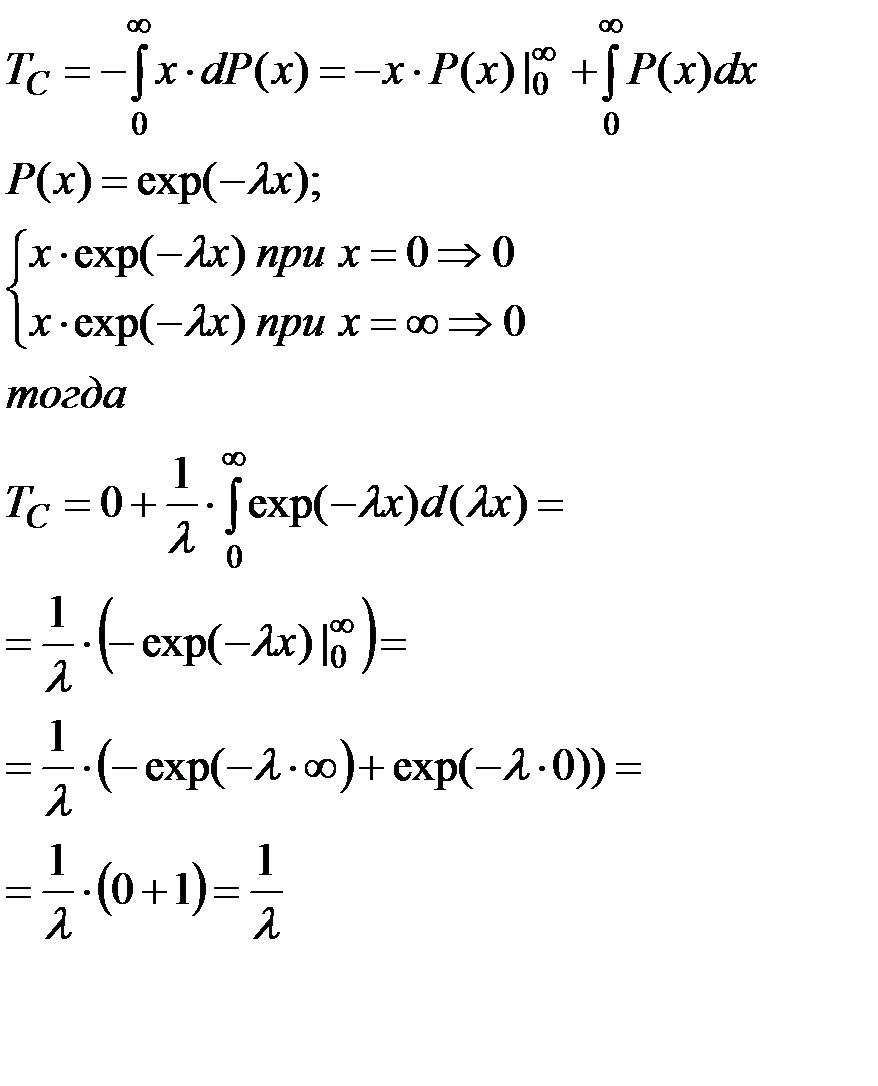 (2.23)
(2.23)
Дисперсия D[T] случайного времени Т безотказной работы системы:
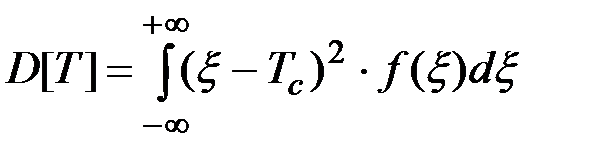 (2.24)
(2.24)
где Т –– случайное время безотказной работы системы; Тс –– математическое ожидание времени работы системы до отказа; f(x) –– дифференциальный закон распределения случайного времени безотказной работы системы.
Для случая распределения случайной величины по закону Пуассона при постоянном значении интенсивности отказов 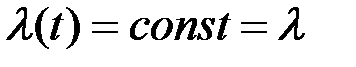 :
:
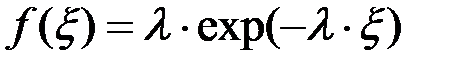 (2.25)
(2.25)
Тогда формула для вычисления дисперсии D[T] может быть выведена на основании следующих преобразований с учетом того, что время не может быть отрицательным, т.е. в (2.22) нижний предел интегрирования равен нулю:
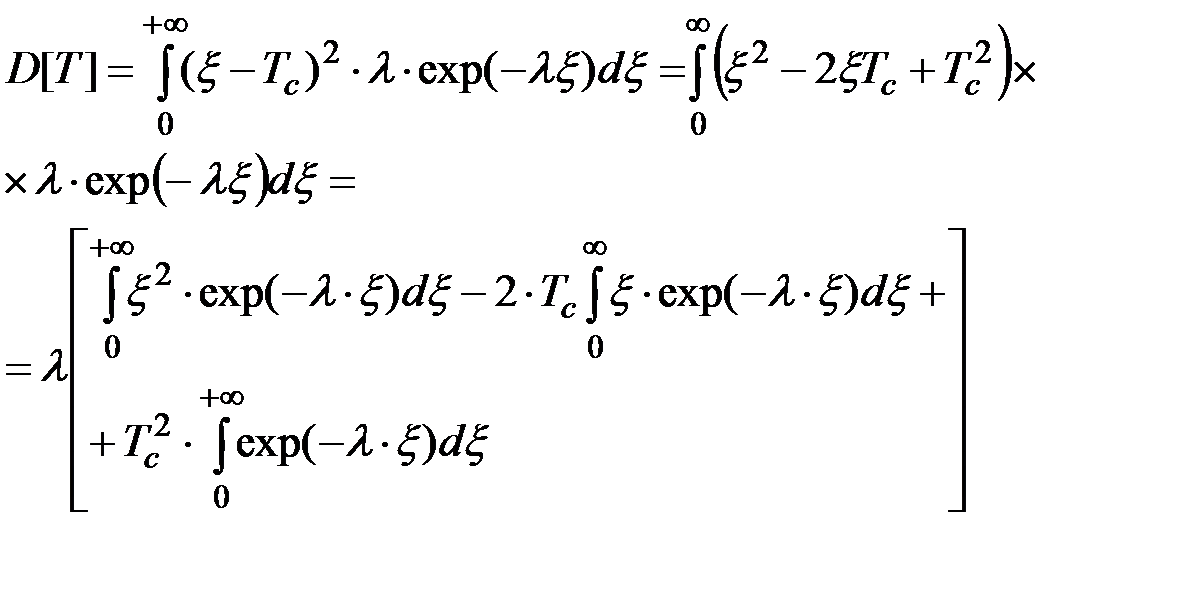 (2.26)
(2.26)
Для вычисления этих интегралов вводятся обозначения:
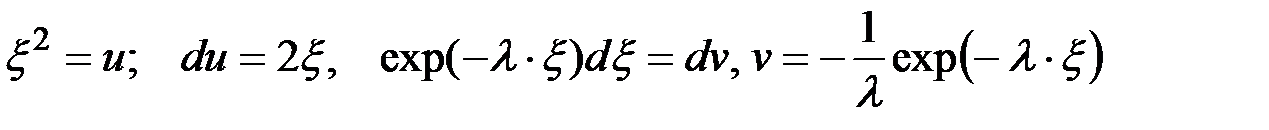 ,
,
тогда, пользуясь формулой интегрирования по частям, имеем:
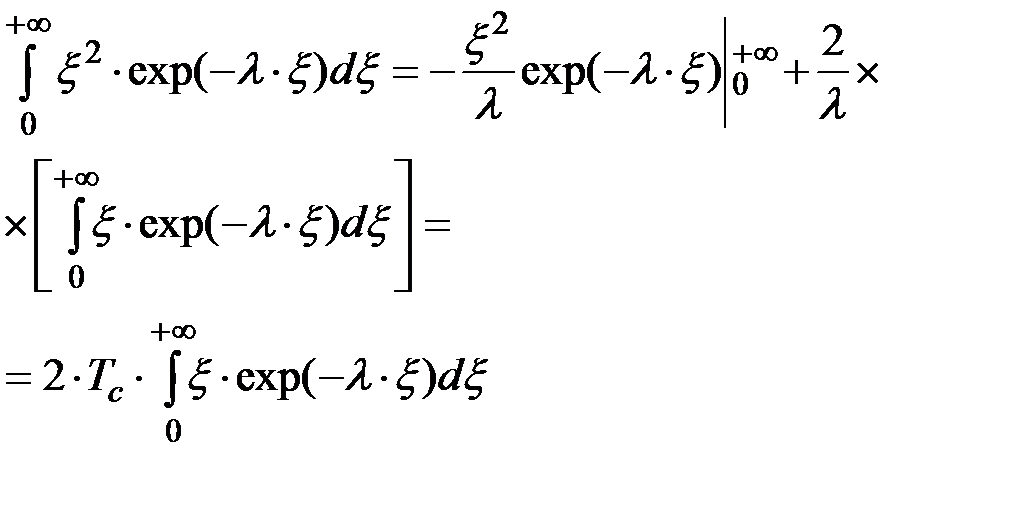
Подставляя это выражение в (2.24), получим:
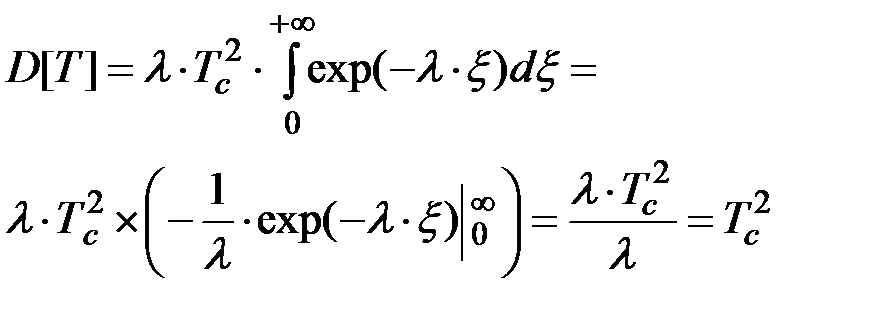 (2.27)
(2.27)
2.2. Характеристики технических систем, используемые в теории надежности.
Коэффициент стабильности надежности Kст –– отношение значений вероятностей исправной работы устройства для двух произвольных периодов времени;
Kст 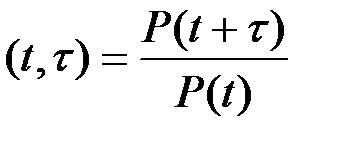 (2.28)
(2.28)
Если коэффициент стабильности равен единице, то надежность системы на участке t остается неизменной.
На практике часто используется показатель изменения надежности:
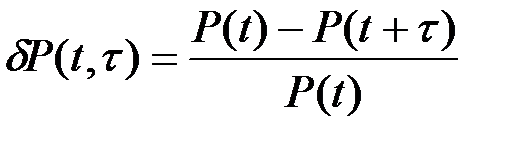 (2.29)
(2.29)
P(t) –– вероятность нахождения системы в исправном состоянии в течение времени T ³ t.
Коэффициент стоимости эксплуатации Kсэ –– отношение стоимости одного года эксплуатации системы Сэ к стоимости изготовления системы С0:
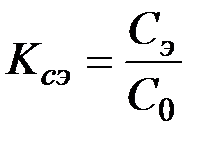 (2.30)
(2.30)
В корректной постановке Сэ=Сэ(t) и чем больше срок эксплуатации системы, тем выше износ ее элементов и тем выше значение стоимости эксплуатации. Однако зачастую в инженерной практике принимают Сэ=const
Особого внимания заслуживает коэффициент эффективности системы.
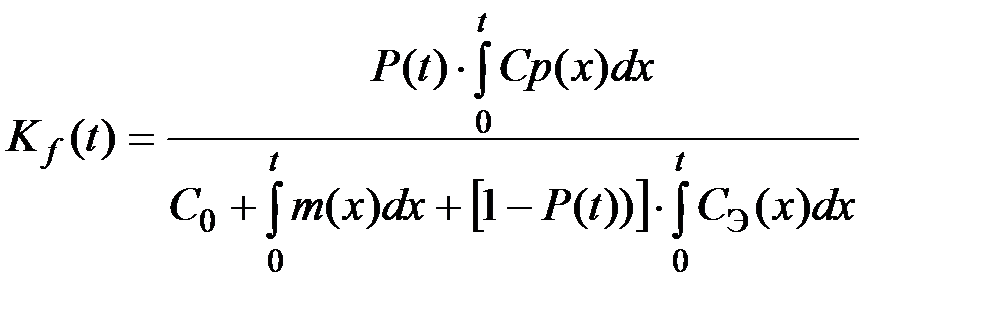 (2.31)
(2.31)
где С0 –– стоимость разработки (создания) системы; P(t) –– надежность технической системы; Cp(x) –– мгновенное значение прибыли; m(x) –– мгновенное значение платы за аренду (за загрязнение окружающей среды); Cэ(х) –– мгновенное значение расходов на эксплуатацию (ремонт) системы.
Рассмотрим расчетный пример
Пример 2.1.
Для расчетного примера приняты следующие значения величин:
Интенсивность отказов l=0.05 (1/год); стоимость С0=150 (усл. ед.); польза Ср(х)=40 (усл.ед.); амортизация m(x)=3 (усл. ед.); эксплуатация 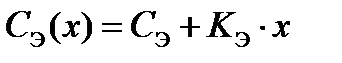 , где СЭ=1(усл. ед.), КЭ=0.5 (усл. ед.), что после интегрирования приводит к выражению:
, где СЭ=1(усл. ед.), КЭ=0.5 (усл. ед.), что после интегрирования приводит к выражению:
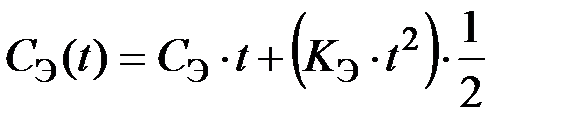
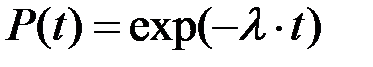
Результаты расчетов по программе в Matlab:
%Вычисление рационального срока эксплуатации системы
t=0:0.1:30;
c0=150;L=0.05;cp=40.*t;m=3.*t;ce=t+0.25.*t.^2;
p=exp(-L.*t);
A=p.*cp;
B=c0+m+(1-p).*ce;
Kf=A./B;
plot(t,Kf);
K1=1;
plot(t,Kf,'k-',t,K1,'k+','LineWidth',3)
xlabel('t')
ylabel('Kf')
grid on
title('Kf')
Рис. 2.4. Изменение коэффициента эффективности системы и ее надежности.
Как видно из графиков рис. 2.4 срок рентабельности технической системы находится в пределах от 6 лет до 20 лет, т.е. определяется тем временем, в пределах которого числитель (2.31) превышает знаменатель или «прибыль» системы выше расходов на ее создание и эксплуатацию.
2.3. Марковские процессы, потоки событий. Элементы теории массового обслуживания.
Говорят, что в физической системе происходит случайный процесс, если она с течением времени может под влиянием случайных факторов переходить из состояния в состояние.
Потоком событий называется последовательность событий, наступающих одно за другим в случайные моменты времени.
Плотностью (интенсивностью) потока называется среднее число событий в единицу времени.
Большое значение имеют процессы, для которых состояние системы изменяется в случайные моменты времени. Особую роль играют такого рода процессы, для которых выполнены три условия:
стационарность,
отсутствие последействия,
ординарность.
Процессы, удовлетворяющие всем этим условиям, называются простейшими или однородными процессами Пуассона.
В перечисленные условия вкладывается следующий смысл.
Стационарность означает, что для любой группы из конечного числа непересекающихся промежутков времени вероятность наступления определенного числа событий на протяжении каждого из них зависит от этих чисел и от длительности промежутков времени, но не зависит от сдвига всех временных отрезков на одну и ту же величину. В частности, вероятность появления m событий в течение промежутка от t до t +Dt не зависит от t и является функцией только аргументов m, Dt.
Отсутствие последействия означает, что вероятность наступления m событий в течение интервала времени (t, t+Dt) не зависит от того, сколько раз и как появились события ранее. Это предположение означает, что условная вероятность появления m событий на промежутке (t, t+Dt) при любом предположении о наступлении событий до момента t совпадает с безусловной вероятностью. Отсутствие последействия означает взаимную независимость появления того или иного числа событий в непересекающиеся моменты времени.
Ординарность выражает собой требование практической невозможности появления двух и более событий за малый промежуток времени Dt. Точнее, это означает следующее: обозначим через 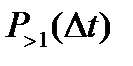 вероятность появления более, чем одного события за этот малый промежуток времени. Тогда условие ординарности состоит в следующем:
вероятность появления более, чем одного события за этот малый промежуток времени. Тогда условие ординарности состоит в следующем:
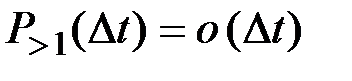
Если Pk(t) –– вероятность появления ровно k событий за время t:
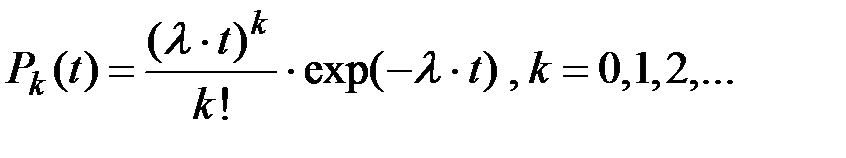
то P0(t) –– можно интерпретировать как вероятность того, что длительность промежутка времени между двумя последовательными появлениями событий окажется большей t.
Если события образуют пуассоновский поток, то число m событий, попадающих на любой интервал времени (t0, t0+t) распределено по закону Пуассона:
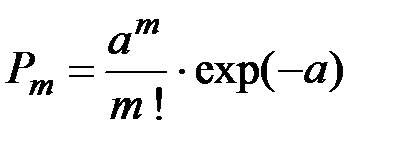 (2.32)
(2.32)
где a –– математическое ожидание числа событий, попадающих на этот участок:
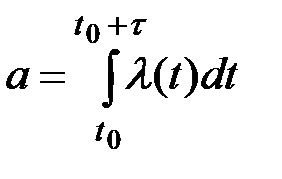 (2.33)
(2.33)
l(t) –– плотность (интенсивность) потока.
Если l(t)=const , пуассоновский поток называется стационарным пуассоновским или простейшим потоком.
Расстояние (временной интервал) Т между двумя соседними событиями в простейшем потоке есть непрерывная величина, распределенная по показательному закону с плотностью:
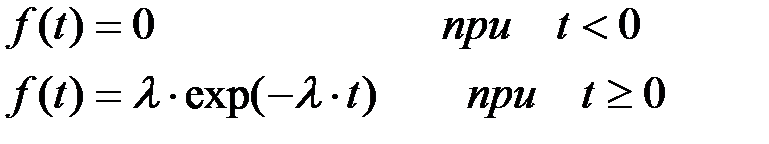 (2.34)
(2.34)
Для случайной величины Т, распределенной по показательному закону, справедливы характеристики:
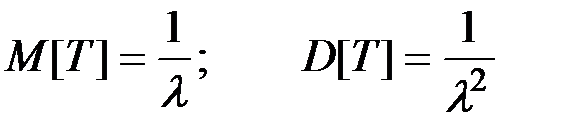 (2.35)
(2.35)
В физической системе S происходит случайный процесс, если она с течением времени может под влиянием случайных факторов изменять свое состояние.
Случайный процесс, протекающий в системе, называется процессом с дискретным временем, если переходы системы из состояния в состояние возможны только в определенные моменты времени t1, t2,…tn,… Если переходы возможны в любые произвольные моменты времени, процесс называется процессом с непрерывном временем.
Случайный процесс с дискретным состоянием называется марковским, если все вероятностные характеристики в будущем зависят только от того, в каком состоянии находится этот процесс в настоящее время и не зависят от того, каким образом этот процесс протекал в прошлом. Будущее зависит от прошлого только через настоящее. Если процесс марковский, то все потоки событий, переводящие систему из состояния в состояние, являются пуассоновскими.
При анализе случайных процессов с дискретным состоянием удобно пользоваться геометрической схемой, называемой графом состояний, который изображает возможные состояния системы и возможные переходы из состояния в состояние.
Каждое состояние системы обозначается квадратом или кружком, а возможные переходы системы из состояния в состояние –– стрелками, соединяющими квадраты или кружки. Заметим (рис. 2.5), что стрелками отмечаются только непосредственные переходы системы из состояния в состояние.
Например, если система из состояния S0 может перейти в состояние S3 только через состояние S1 или S2 , то стрелками отмечаются только переходы из S0 в S1 и из S0 в S2, а не из состояния S0 в S3.
| S0 |
| S2 |
| S3 |
| S1 |
Рис. 2.5. Граф состояний системы.
В теории надежности чаще встречаются ситуации, когда переходы системы из состояния в состояние происходят в случайные моменты времени, которые заранее предсказать невозможно. Для описания таких процессов в ряде случаев может быть применена схема марковского процесса с дискретным состоянием и непрерывным временем.
Система S называется системой с дискретным состоянием, если она имеет счетное множество возможных состояний (число состояний можно перенумеровать) S1, S2,…,Sn,… и переход из одного состояния в другое осуществляется скачком. В дальнейшем рассматриваются только системы с дискретным состоянием.
Состояние системы называется «состоянием без выхода», если из него невозможен переход ни в какое другое состояние.
Для описания случайного процесса, протекающего в системе, зачастую пользуются вероятностями состояний:
p1(t), p2(t),…,pn(t),
где pk(t) –– вероятность того, что в момент t система находится в состоянии Sк.
Вероятности pk(t) удовлетворяют условию:
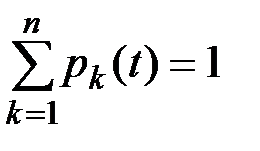
Введем в рассмотрение плотность lij вероятностей перехода системы из состояния Si в состояние Sj.
| t |
| t+∆t |
| ∆t |
| T |
Рис. 2.6. Представление режима работы системы во времени.
Пусть система (рис.2.6) в момент t находится в состоянии Si. Рассмотрим элементарный участок Dt, примыкающий к моменту t.
Назовем плотностью вероятностей (или интенсивностью) перехода из состояния Si в состояние Sj величину lij как предел отношения вероятности перехода от состояния Si в состояние Sj за время Dt к продолжительности этого промежутка времени Dt:
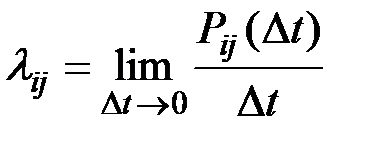 (2.36)
(2.36)
где Pij(Dt) –– вероятность того, что система, находившаяся в момент t в состоянии Si , за время Dt перейдет в состояние Sj (справедливо только для i¹j).
При малом значении временного интервала Dt вероятность Pij(Dt) с точностью до бесконечно малых высшего порядка малости равна:
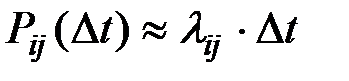 (2.37)
(2.37)
Если все интенсивности перехода lij не зависят от времени, марковский процесс называют однородным, в противном случае –– процесс называется неоднородным.
Пусть нам известны все lij для всех пар (Si, Sj) . Построим граф состояний системы и против каждой стрелки поставим соответствующую плотность вероятности перехода (рис. 2.7.3). Такой граф называется размеченным графом состояний.
| Si |
| Sj |
| Sk |
| lij |
| ljk |
Рис.2.7 Пример построения размеченного графа.
При наличии размеченного графа состояний системы, можно определить вероятности состояний P0(t), P1(t), P2(t)…как функции времени, а именно, эти вероятности удовлетворяют дифференциальным уравнениям Колмогорова.
Продемонстрируем методику вывода системы дифференциальных уравнений Колмогорова на конкретном примере (рис.2.8).
Пусть система имеет пять состояний S0, S1, S2, S3, S4. Поставим задачу найти одну из вероятностей состояния, например, P0(t). Это есть вероятность того, что в момент t система будет находиться в состоянии S0.
Придадим моменту t малое приращение Dt и найдем вероятность того, что в момент t+Dt система будет находиться в состоянии S0.
Реализация такого события возможна двумя путями:
а) система не изменит своего состояния за промежуток времени Dt;
б) система, находясь в момент t в состоянии S3, перейдет за Dt в состояние S0.
Вариант а)реализуется, если в момент t система с вероятностью P0(t) находилась в состоянии S0 и не перешла из состояния S0 в состояние S1. Вероятность последнего события может быть вычислена (для малых значений Dt) по формуле:
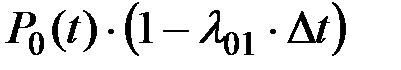 ,
,
где P0(t) –– вероятность нахождения системы в момент t в состоянии S0, l01×Dt –– вероятность перехода системы за промежуток времени Dt из состояния S0 в состояние S1, (1-l01×Dt) –– вероятность неперехода системы за интервал времени Dt из состояния S0 в состояние S1.
| l01 |
| S0 |
| l30 |
| l42 |
| S2 |
| S3 |
| l13 |
| S4 |
| l12 |
| l34 |
| S1 |
Рис. 2.8. Фрагмент размеченного графа технической системы.
Вариант б)реализуется в том случае, если система в момент t находилась с вероятностью Р3(t) в состоянии S3 и за интервал времени Dt перешла в состояние S0:
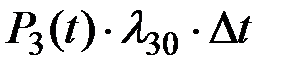 ,
,
где l30×Dt –– вероятность перехода за малый интервал времени Dt системы из состояния S3 в состояние S0.
Поскольку система в момент t+Dt могла находиться в состоянии Р0 только или первым или вторым способом, то получаем:
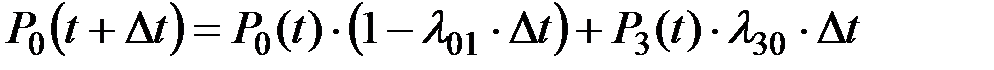
откуда:
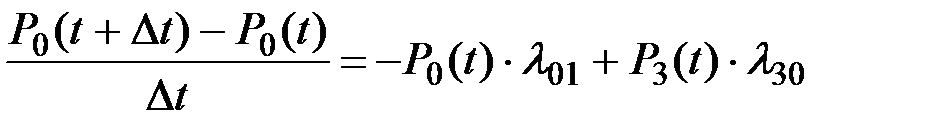 (2.38)
(2.38)
или:
 (2.39)
(2.39)
Рассмотрим состояние S1 и выведем уравнение для определения вероятности P1(t) того, что в момент t+Dt система будет находиться в состоянии S1.
Реализация такого состояния возможна, если:
- система находилась в момент t в состоянии S0 и за время Dt перешла в состояние S1. Вероятность такого перехода определяется произведением соответствующих вероятностей:
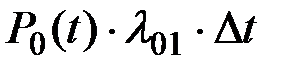
- система в момент t находилась в состоянии S1 и за интервал Dt своего состояния не изменила, т.е. не перешла ни в состояние S2, ни в состояние S3. Оценим вероятность осуществления этого варианта.
Вероятность того, что система, находясь в состоянии S1, перейдет за время Dt в состояние S2 или S3:
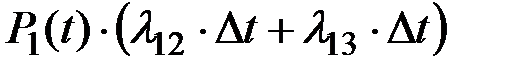
Вероятность неперехода системы из состояния S1 ни в одно из этих состояний:
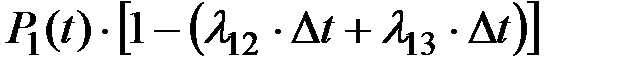
Окончательно получим:
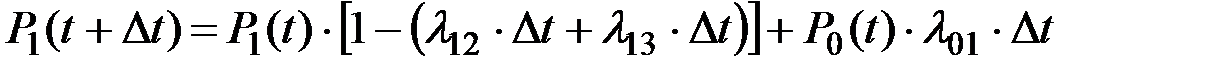
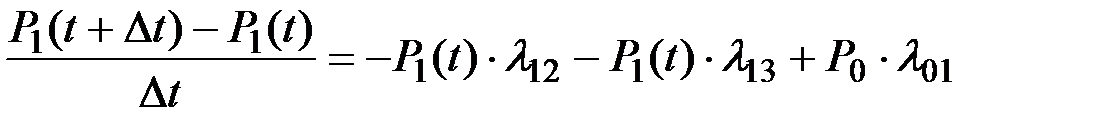
Или, при стремлении Dt к нулю, имеем окончательно:
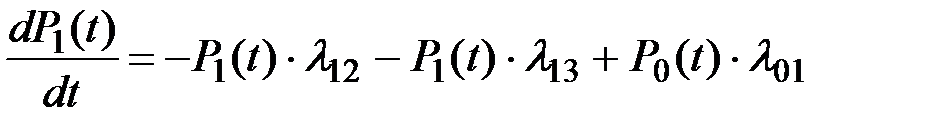 (2.40)
(2.40)
Аналогичным образом могут быть получены зависимости системы дифференциальных уравнений Колмогорова для всех остальных состояний рассматриваемой системы.
В итоге получим систему дифференциальных уравнений:
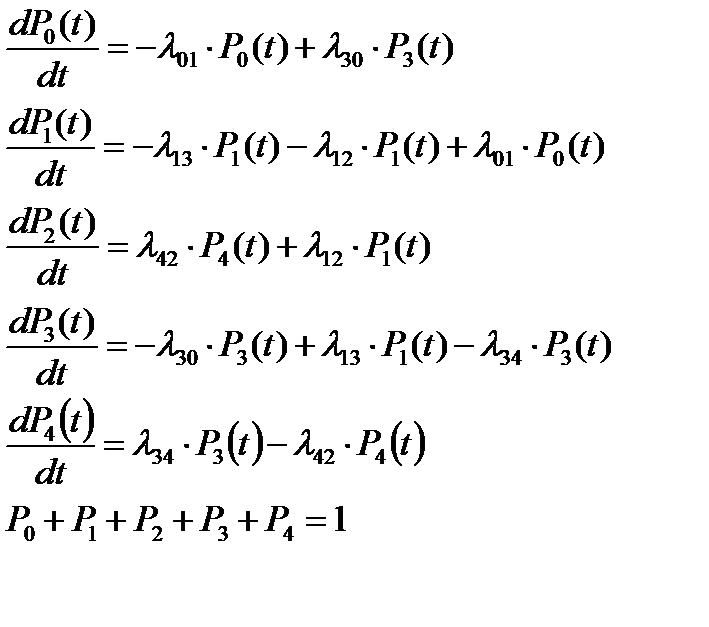 (2.41)
(2.41)
Интегрирование этой системы дифференциальных уравнений при начальных, условиях, например,
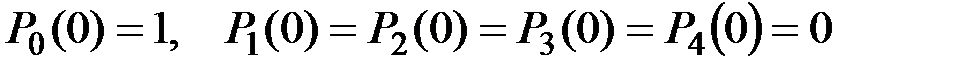
дает искомые функции вероятностей состояний: 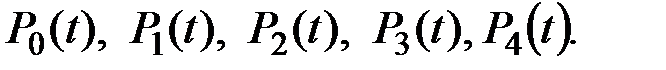
Все уравнения (2.41) построены по определенному правилу, зная которое можно выписывать систему для размеченного графа почти автоматически:
· в левой части каждого уравнения стоит производная 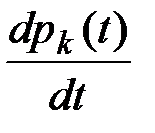 ,
,
· в правой части содержится столько членов, сколько стрелок связано непосредственно с данным k –– м состоянием,
· член правой части уравнения имеет знак плюс, если стрелка ведет в данное состояние и знак минус,если стрелка выходит из данного состояния,
· каждый член правой части уравнения равен плотности потока событий, переводящего системупо данной стрелке, умноженной на вероятность того состояния, изкоторого исходит стрелка.
Эти правила составления системы дифференциальных уравнений Колмогорова справедливы для любой непрерывной марковской цепи.
Например.
Рис. 2.9. Размеченный граф системы с дискретным состоянием
и непрерывным временем.
Система дифференциальных уравнений такой системы имеет вид:
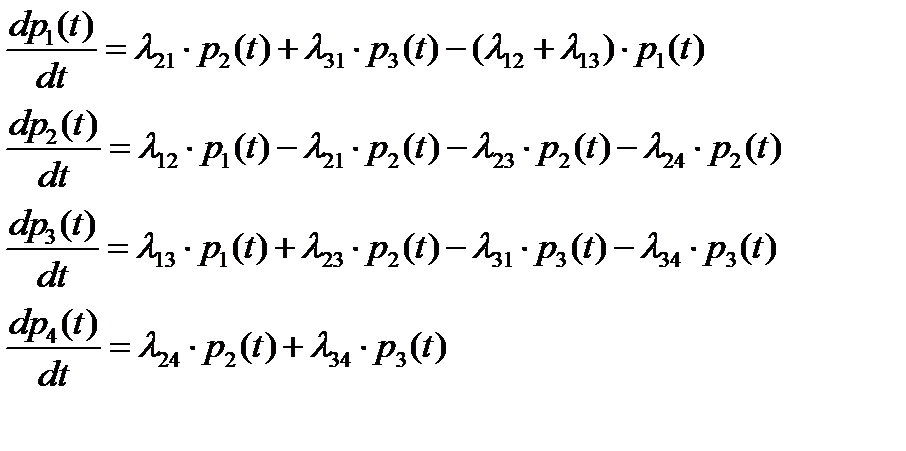 (2.42)
(2.42)
Начальные условия для интегрирования такой системы отражают состояние системы в начальный момент времени. Так, если в момент t=0 система была в состоянии Sk , то полагают:
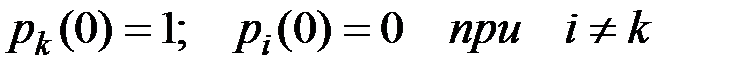
Число уравнений в системе может быть уменьшено на единицу, если учесть условие, что для любого t (для рассматриваемой системы):
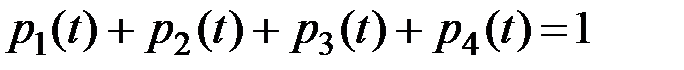
Дата добавления: 2019-02-07; просмотров: 1893;
