Определение надежности технических систем при постоянно включенном резерве («горячее» резервирование).
4.1. Количественные показатели надежности резервированной системы с постоянно включенным резервом.
Будем исследовать надежность технической системы, состоящей из одного основного и m резервных устройств, т.е. содержащей m+1 устройство. При этом принимаются следующие допущения:
- все устройства (основное и резервные) системы постоянно включены в работу и эксплуатируются в абсолютно одинаковых условиях нагружения;
- отказ любого устройства не влияет на работу остальных работоспособных устройств;
- отказ системы происходит в момент отказа последнего из (m+1) устройств;
- в момент включения системы в работу (t=0) все устройства работоспособны;
- все устройства (основное и резервные) абсолютно идентичны по показателям надежности;
- отказы устройств представляют собой простейший поток случайных событий;
- ремонт рассматриваемой технической системы невозможен.
Принятые допущения почти никогда не реализуются в практике, но они удобны для выводов основных показателей надежности технической системы, резервированной по способу постоянно включенного резерва.
Предполагая, что каждое устройство системы состоит из n элементов, отказы которых являются случайными и независимыми событиями, вероятность pj(t) безотказной работы любого из (m+1) устройства можно принять равной произведению вероятностей безотказной работы его отдельных элементов:
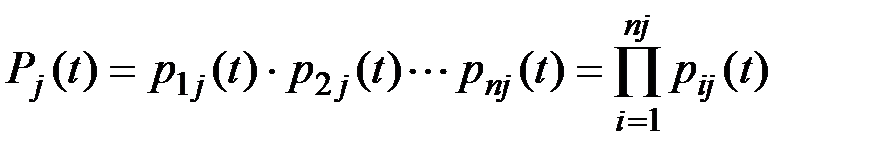
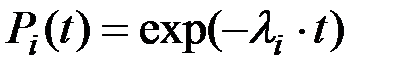(4.1)
где pij(t) –– вероятность безотказной работы i-го элемента j-го устройства в течение времени t; nj –– число элементов в j-м устройстве.
Учитывая принятую гипотезу об идеальности коммутаторов, вероятность отказа QC(t) технической системы будет равна:
(4.2)
Если рассматривается система с однотипными устройствами, то все Qj(t) равны между собой и можно принять обозначение:
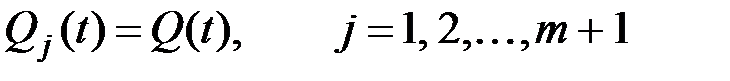(4.3)
тогда вероятность отказа системы в течение времени t может быть определена выражением:
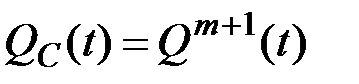
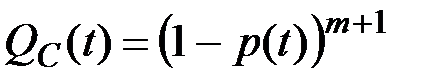(4.4)
где р(t) –– надежность одного (любого) устройства технической системы.
С учетом (4.1) можно записать:
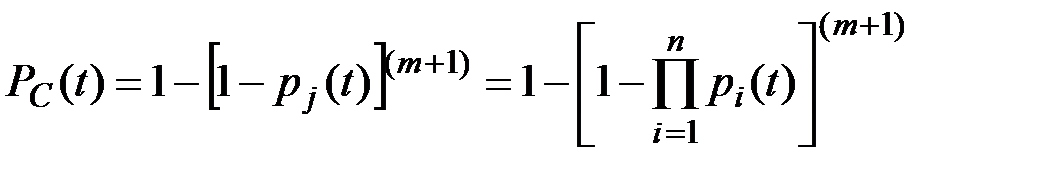(4.5)
Формулы (4.2)…(4.5) просты и удобны при вычислении различных показателей надежности резервированной системы. Так, если задана надежность р(t) резервирующих устройств (включая основное), то можно найти необходимую кратность резервирования, чтобы обеспечить требуемую надежность Рmp системы в целом:
из неравенства
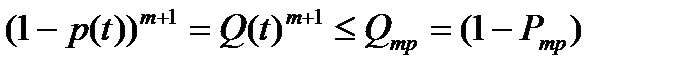(4.6)
получим
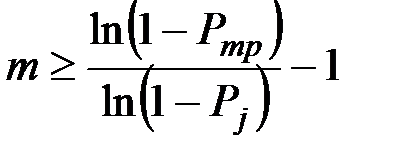(4.7)
Пример 4.1
Для достижения требуемой надежности системы Ртр= 0.99 или 0.95 к заданному моменту времени t при известных значениях надежности одного устройства рj(t) Î [0.1 , 0.8], необходимо определить требуемое число резервных устройств m (при общем их числе m+1) с использованием пакета Matcad.
| О п р е д е л е н и е т р е б у е м о й к р а т н о с т и р е з е р в и р о в а н и я |
Результаты решения можно свести в таблицу.
Таблица 4.1.
Требуемая кратность резервирования
| Надежность резервных PJ | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 |
| m (Pтр1=0,99) | ||||||||
| m (Pтр=0,95) |
В свете принятой гипотезы о простейшем потоке отказов, выражение для определения надежности pi(t) i-го элемента, входящего в состав одного из резервирующих устройств технической системы будет иметь вид:
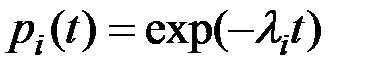(4.8)
где li –– интенсивность отказов i-го элемента устройства.
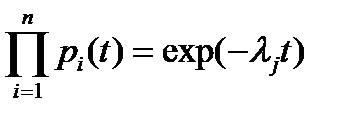(4.9)
где lj –– интенсивность отказов устройства (любого)
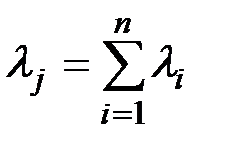(4.10)
С учетом выражений (4.8)…(4.10) надежность PC(t) и ненадежность QC(t) системы, резервированной по способу «горячего» резерва и состоящей из одного основного и m резервных однотипных устройств могут быть вычислены по формулам:
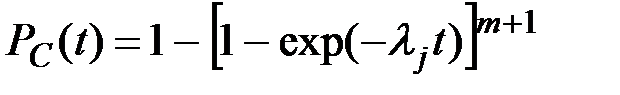(4.11)
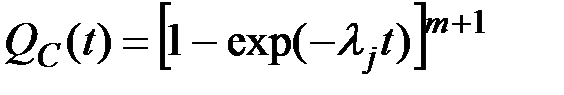(4.12)
Среднее время ТС безотказной работы системы определим из следующих рассуждений. В общем виде среднее время определяется как математическое ожидание случайной величины, имеющей плотность распределения f(t).
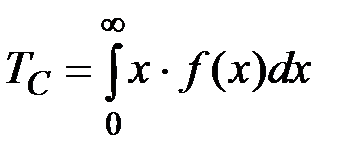(4.13)
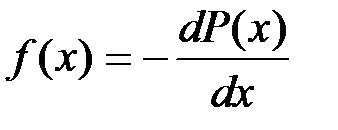(4.14)
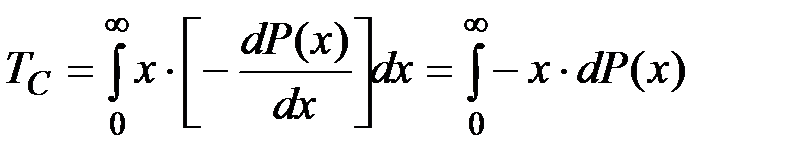
Введем обозначения
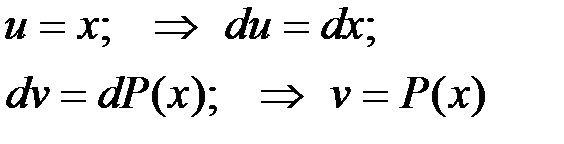
и применяем интегрирование по частям
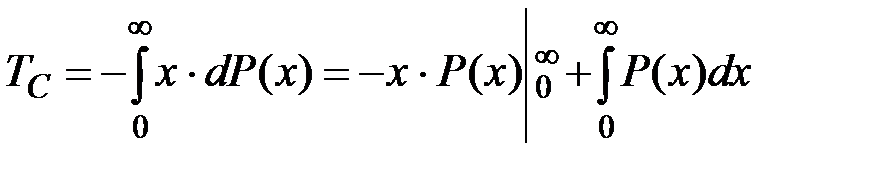
Поскольку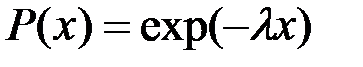 
убывает при x ® ¥ быстрее, чем возрастает x, следовательно,
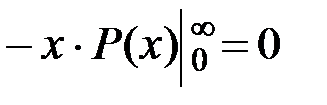(4.15)
Окончательно получаем
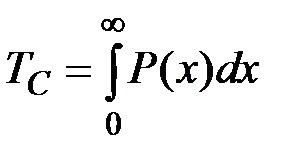(4.16)
С учетом (4.11), получаем:
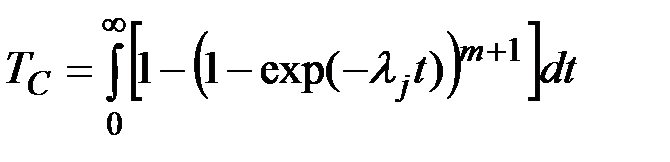(4.17)
Введем обозначение: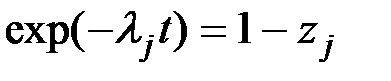 
тогда после дифференцирования получим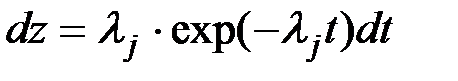 
откуда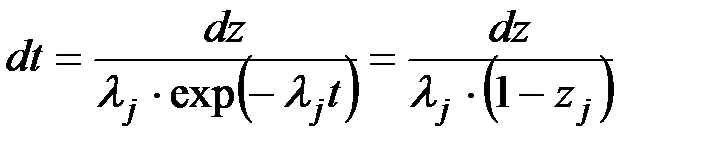 
при этом происходит изменение пределов интегрирования. При t=0 zj=0. При t=¥ zj=1, и выражение (4.17) с учетом выкладок Приложения 1 приобретает вид:
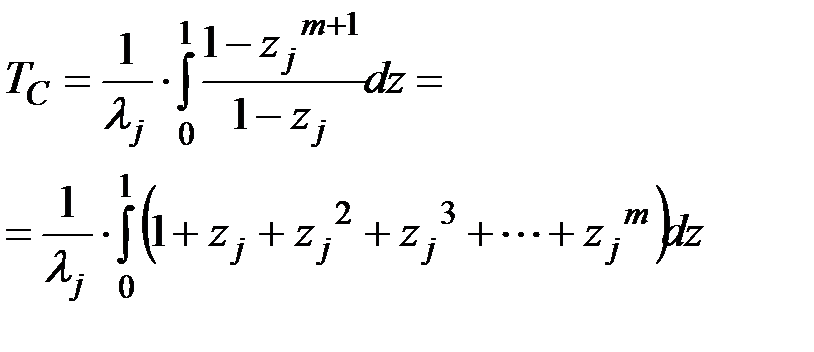(4.18)
Далее
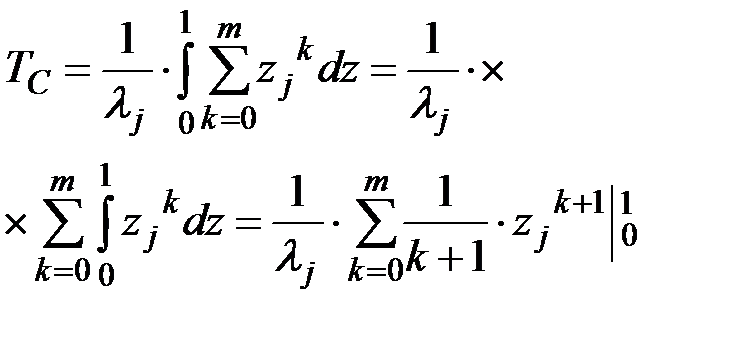(4.19)
Подставив пределы интегрирования, получим окончательное выражение для среднего времени безотказной работы системы, при «горячем» резервировании:
| В ы ч и с л е н и е о ж и д а е м о г о в р е м е н и TC(m) р а б о т ы с и с т е м ы д о о т к а з а п р и к р а т н о с т и р е з е р в и р о в а н и я m о т 1 д о 5 в Mathcad |
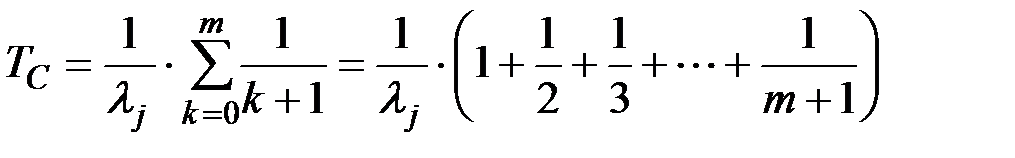(4.20)
Пример 4.2.
Размерность ожидаемого времени работы системы до отказа определяется размерностью интенсивности отказов устройств λJ.
Частота и интенсивность отказов резервированной системы вычисляется на основе выражений:
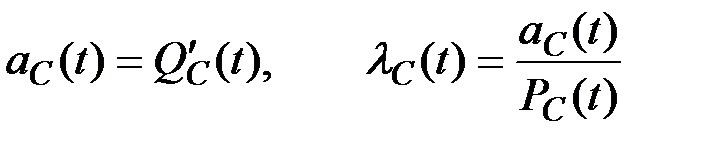(4.21)
Используя (4.11), (4.12), получим:
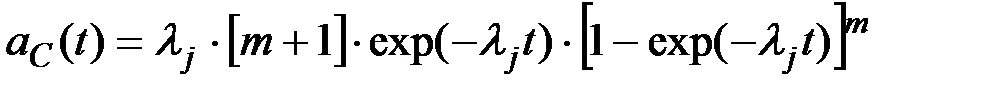(4.22)
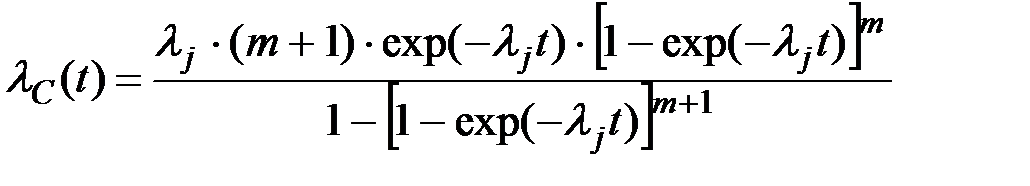(4.23)
Рис. 4.2. Изменение частоты отказов в течение времени эксплуатации системы при различной кратности резервирования и интенсивности отказов устройств lj=0.015 1/час.
Рис. 4.3. Изменение интенсивности отказов системы в течение времени ее эксплуатации при различной кратности резервирования и интенсивности отказов устройств lj=0.015 1/час.
Пример 4.3.
Рассматривается система, состоящая из четырех последовательно функционирующих блоков обеспечения безопасности. Известны вероятности отказа Q каждого блока и их масса x.
По требованиям эксплуатации системы общая масса системы безопасности не должна превышать заданного значения ММ.
Требуется определить, какие блоки следует резервировать для получения максимальной надежности системы при ограничении на общую массу.
Решение примера 4.3 в среде Matlab [16]
MM=25; допустимый максимальный вес системы обеспечения безопасности
x=[2.5 2.0 3.5 1.5]; веса устройств системы обеспечения безопасности
Q=[0.03 0.1 0.04 0.02]; ненадежность устройств системы обеспечения безопасности
p1=0;
for m1=1:5
for m2=1:5
for m3=1:5
for m4=1:5
if m1*x(1)+m2*x(2)+m3*x(3)+m4*x(4)<MM
p=(1-Q(1)^m1)*(1-Q(2)^m2)*(1-Q(3)^m3)*(1-Q(4)^m4);
end
if p>p1
p1=p;ma1=m1;ma2=m2;ma3=m3;ma4=m4;
end
end
end
end
end
m=[ma1 ma2 ma3 ma4]
MA=[ma1*x(1) ma2*x(2) ma3*x(3) ma4*x(4)]
MMA=sum(MA)
p1
p0=(1-Q(1))*(1-Q(2))*(1-Q(3))*(1-Q(4))
mm=[ma1-1 ma2-1 ma3-1 ma4-1]
m = 2 3 3 2 общее число устройств в каждом блоке
MA = 5.0000 6.0000 10.5000 3.0000
MMA = 24.5000 общая масса системы безопасности
p1 = 0.9976 надежность системы после резервирования
p0 = 0.8213 надежность системы до резервирования
mm = 1 2 2 1 число резервных устройств для каждого блока
Подводя итог, можно констатировать:
· «горячее» резервирование повышает вероятность безотказной работы системы в сравнении с надежностью нерезервированной системы, причем с увеличением кратности резервирования надежность технической системы повышается;
· среднее время безотказной работы резервированной системы с увеличением кратности резервирования растет медленно;
· частота отказов резервированной системы вне зависимости от кратности резервирования имеет нулевое значение в начальный момент времени работы системы, имеет максимум и стремится к частоте отказов нерезервированной системы при достаточно больших значениях ljt; максимум функции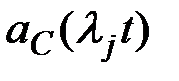 
находится в точке 
;
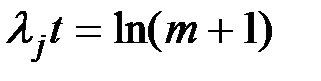· интенсивность отказов резервированной системы также равна нулю в момент включения системы в работу и асимптотически приближается к интенсивности отказов нерезервированной системы при больших значениях ljt.
Из приведенных выводов становится очевидным, что времена возникновения отказов резервированной системы нельзя отнести к стационарным потокам, хотя времена отказов резервных устройств являются простейшим потоком случайных событий. Это означает, что в общем случае среднее время безотказной работы и интенсивность отказов системы не равны соответственно среднему времени между соседними отказами и средней частоте отказов системы. Поэтому оценивать надежность резервированной системы с помощью среднего времени безотказной работы и интенсивности отказов системы можно только до первого ее отказа. Оценивать надежность резервированных систем длительного использования, работающих в режиме замены отказавших устройств следует на основе вычислений среднего времени между соседними отказами и средней частоты отказов, несмотря на то, что времена отказов резервных устройств удовлетворяют условиям простейшего потока случайных событий.
Вопросы для самоконтроля.
Приведите вывод функции изменения вероятности безотказной работы технической системы, резервированной по принципу постоянно включенного резерва для случая, когда основное и резервные устройства одинаковы и для случая, когда все они различны.
Объясните, каким образом можно рассчитать требуемую кратность резервирования технической системы при постоянно включенном резерве.
По каким критериям можно оценить эффективность «горячего» резервирования в сравнении с однотипной нерезервированной системой?
В чем преимущества и недостатки резервирования при постоянно включенном резерве?
5. Нагрузочное резервирование.
Дата добавления: 2019-02-07; просмотров: 616;