Метод интегрирования по частям.
Пусть даны дифференцируемые функции 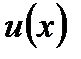 и
и 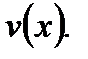 Тогда согласно (3.20) имеем
Тогда согласно (3.20) имеем
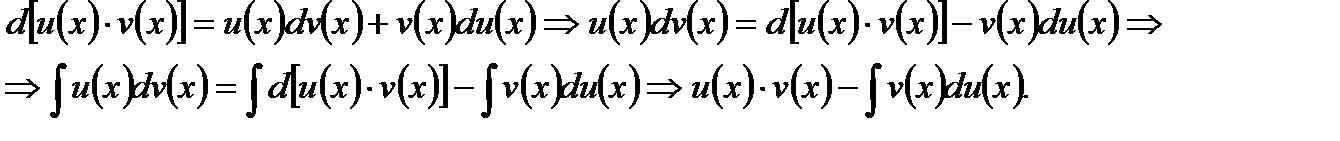 Таким образом, получили так называемую формулу интегрирования по частям в виде
Таким образом, получили так называемую формулу интегрирования по частям в виде
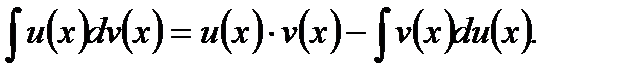 (5.21)
(5.21)
Методом интегрирования по частям (см. 5.21) обычно пользуемся в случаях, когда подынтегральная функция есть произведение многочлена относительно 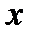 какой-то степени и трансцендентной функции (
какой-то степени и трансцендентной функции ( 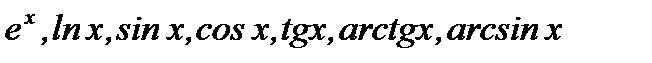 и так далее).
и так далее).
Пример 5.15.Вычислить неопределенный интеграл 
Решение.
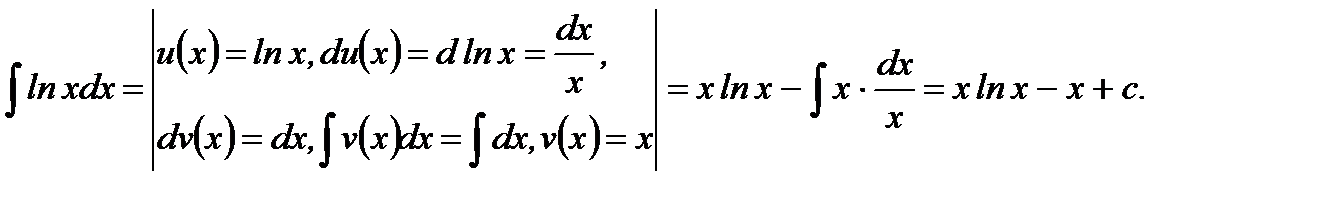
Ответ:
(
)
.
c
1
x
ln
x
xdx
ln
+
-
=
ò
Пример 5.16.Вычислить неопределенный интеграл 
Решение.
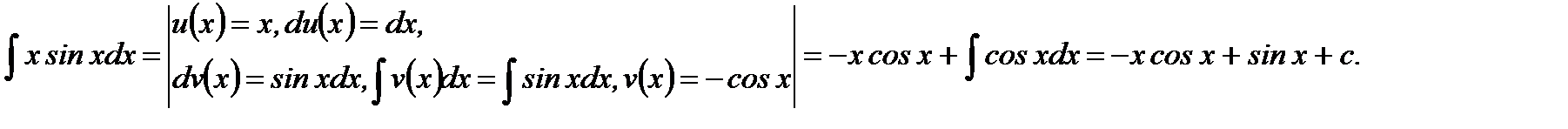
Ответ: 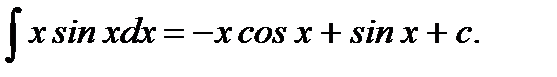

Пример 5.17.Вычислить неопределенный интеграл 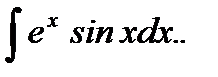
Решение.
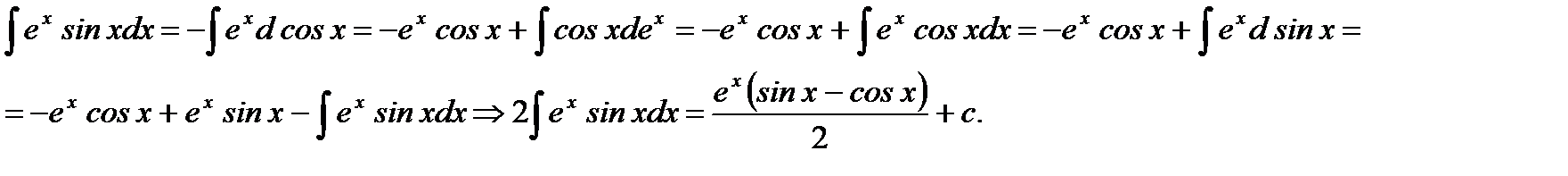
Ответ: 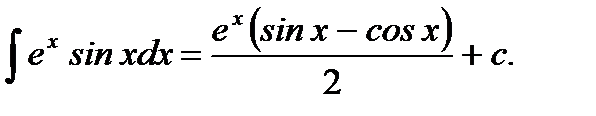

Пример 5.18.Вычислить неопределенный интеграл 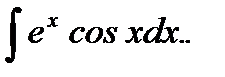
Решение.
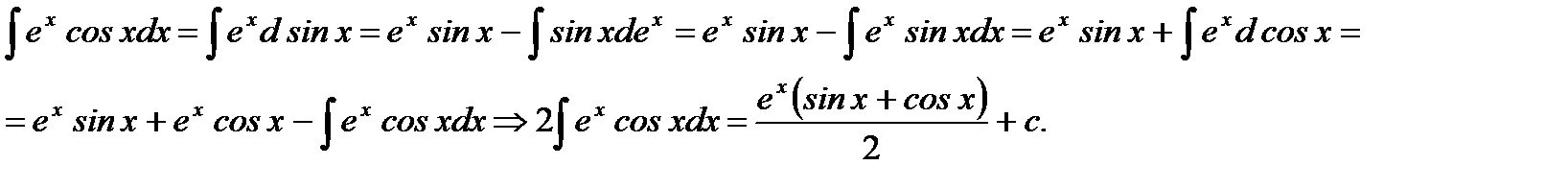
Ответ: 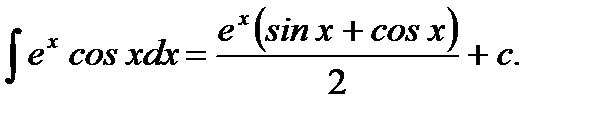

Пример 5.19.Вычислить неопределенный интеграл 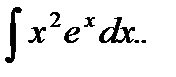
Решение.
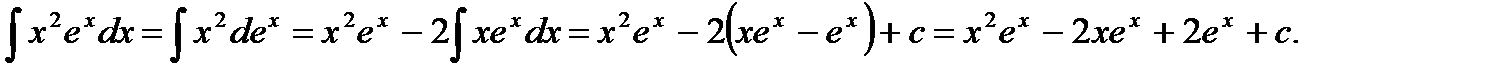
Ответ: 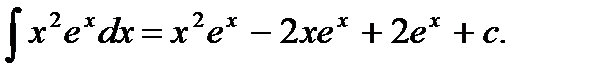
Пример 5.20.Вычислить неопределенный интеграл 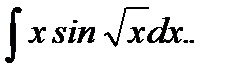
Решение.
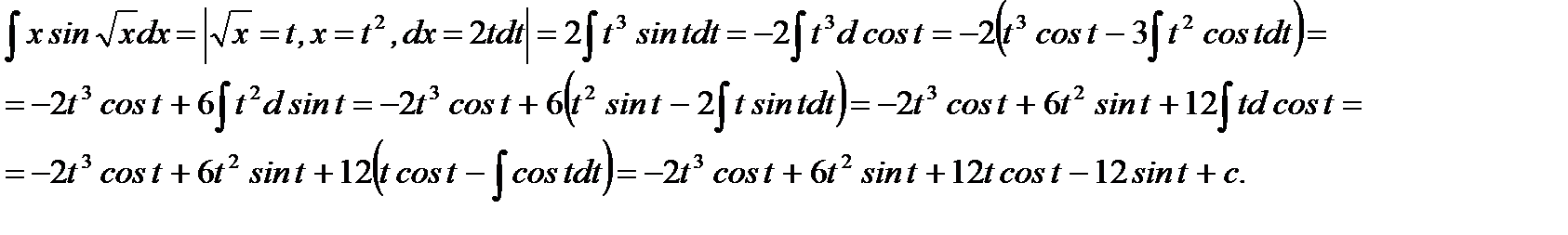
Ответ: 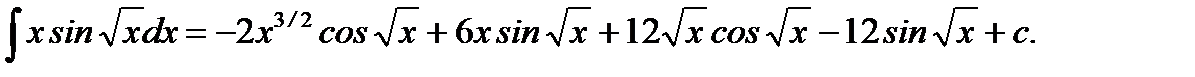
Ниже приведем некоторые формулы (среди них и рекуррентные формулы), которые получаются после вычисления соответствующих интегралов методом интегрирования по частям:
1. 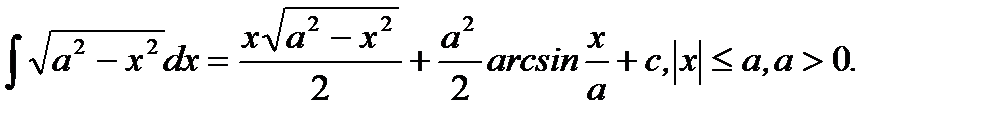 (5.22)
(5.22)
2. 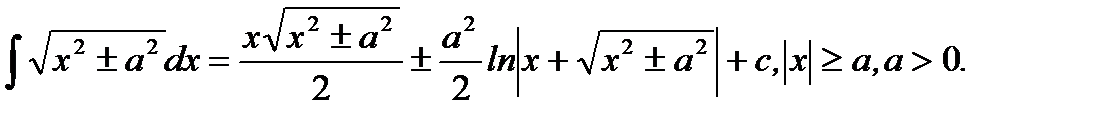 (5.23)
(5.23)
3. 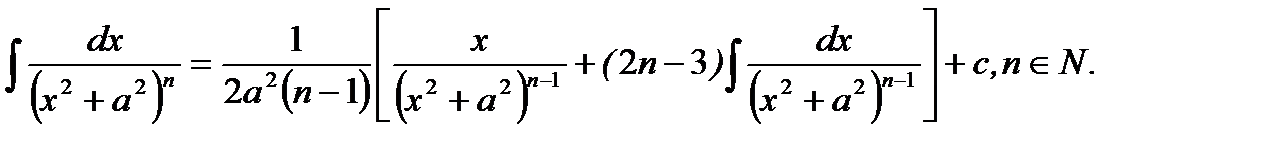 (5.24)
(5.24)
4. 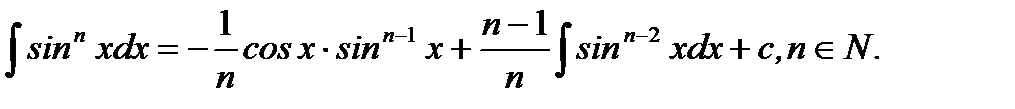 (5.25)
(5.25)
5. 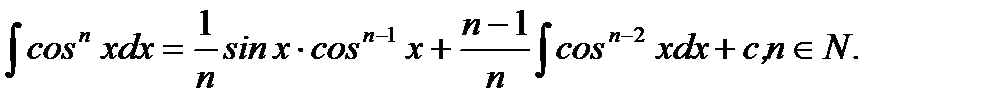 (5.26)
(5.26)
6.  (5.27)
(5.27)
7. 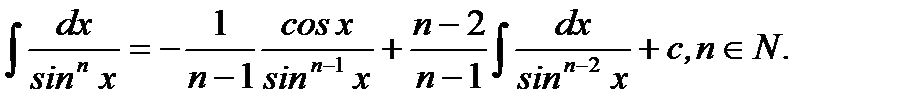 (5.28)
(5.28)
Дата добавления: 2018-11-25; просмотров: 354;
