Дедуктивные методы поиска решений.

Логические модели являются формой представления знаний о проблемных областях с небольшим пространством поиска решений и определенными фактами и знаниями. Они удобны также для формального описания мышления человека, так как часто его рассуждения при решении задач носят дедуктивный характер. Для построения подобных рассуждений система ИИ должна быть способна выводить новые факты исходя из известных ей. Новые логические конструкции и формы создаются применением правил вывода к имеющимся логическим формулам. Основам и методам математической логики посвящены известные монографии [29, 34, 66].

Распространенным типом логических моделей является логика предикатов первого порядка.

Логика предикатов первого порядка является расширением логики высказываний, так как основным объектом здесь является переменное высказывание (предикат), истинность и ложность которого зависят от значений его переменных. Рассмотрим коротко основные правила вывода логики предикатов.

Несколько дополнительных определений:

- Если формула истинна при всех возможных итерациях, то говорят, что она является общезначимой формулой (тавтологией).

- Если формула ложна при всех своих итерациях, то говорят, что она является противоречивой (противоречием). Противоречивая формула невыполнима.

Всякая формула может быть преобразована в нормальную формулу путем использования законов эквивалентных преобразований. Приведем некоторые из них:

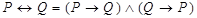
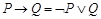
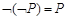- закон двойного отрицания

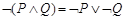; - законы де Моргана.

При логическом выводе в рамках данной формальной системы стоит задача образования из некоторой совокупности исходных ППФ новых формул, которые являются тавтологиями. Эта задача решается с помощью правил вывода и законов.

Modus Ponens (правило заключения или правило дедуктивного вывода) положительная форма условного категорического силлогизма.

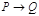; P|— Q ( |— означает “выводимость”).

Modus tollens (Отрицательная форма условно категорического силлогизма).

; |—

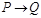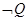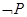
Modus tolleudo Ponens, Modus ponendo tolleus

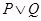
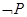|— Q …….. |—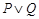

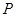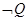
Правило силлогизма (правило ценного умозаключения)

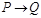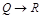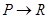, |— и другие.

Формула является выводимой, если она может быть получена из конечной совокупности исходных формул путем конечного количества шагов применения правил вывода. Для сокращения многократного применения основных правил вывода используются специальные правила.

Пусть даны формулы P₁, P₂,… P_n и формула Q. Говорят, что Q есть логическое следствие формул P₁, …, P_n тогда и только тогда, когда для всякой интерпретации I, в которой P₁Ù P₂Ù…ÙP_n истинна, Q также истинна. Здесь P₁, …, P_n называются аксиомами (или постулатами, или посылками) Q.

В дедуктивных системах поиска, по существу, необходимо доказывать, что некоторая формула логически следует из других формул. Утверждение, что формула логически следует из формул, называют теоремой. Проблема поиска решений сводится к проблеме доказательства теоремы, т.е. построения рассуждения, устанавливающего, что формула логически следует из других формул. Доказаны две теоремы, на которых основывается более краткий и простой способ вывода.

Теорема дедукции. Пусть даны формулы P₁,…,P_n и формула Q. Тогда Q есть логическое следствие P₁,…,P_n тогда и только тогда, когда формула

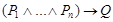общезначима.

Теорема о противоречии. Пусть даны формулы P₁,…,P_n и формула Q. Тогда Q есть логическое следствие P₁,…,P_n тогда и только тогда, когда формула

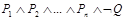противоречива.

Эти две теоремы имеют важное значение, т.к. позволяют прийти к следующему выводу: доказательство того, что отдельная формула есть логическое следствие конечного множества формул, эквивалентно доказательству того, что некоторая связанная с ними формула общезначима или противоречива.

При использовании для вывода теоремы дедукции или теоремы о противоречивости сначала задачу описывают формулой, а затем доказывают, что эти формулы общезначимы или противоречивы.

Помимо рассмотренных эквивалентных формул, в логике предикатов используются другие пары эквивалентных формул, содержащие кванторы. Их также называют законами. В дальнейшем были разработаны более эффективные методы доказательства теорем на базе логики предикатов. Они легли в основу машинных методов поиска доказательств теорем, т.е. логического следования утверждений из исходных.

Метод Эрбрана. Для поиска доказательства методом Эрбрана или методом резолюций (рассмотренным ниже) необходимо выполнить процедуру стандартизации, т.е. преобразования формул в предложения. Предложение – это множество дизъюнктов. Дизъюнкт – это дизъюнкция литер.

В результате стандартизации получаем стандартную форму в виде множества дизъюнктов. При использовании метода Эрбрана к стандартной форме формулы применяют процедуры поиска опровержения. Это делается для удобства реализации поиска, т.е. вместо доказательства общезначимости формулы доказывают, что отрицание формулы противоречиво.

Пусть S – стандартная форма формулы F, представленная в виде множества дизъюнктов. Тогда F противоречива в том случае, когда противоречива S.

Множество дизъюнктов невыполнимо тогда, когда оно ложно при всех интерпретациях на всех областях. Из-за невозможности рассмотрения интерпретаций на всех областях, строится такая область H, что если не существует удовлетворяющей интерпретации в этой области, то ее вообще не существует, т.е. S невыполнимо тогда, когда оно ложно при всех интерпретациях в этой области. Такая область называется универсумом Эрбрана и обозначается H(S).

Недостатком метода Эрбрана является экспоненциальный рост множества. Подробнее метод Эрбана см. [66,14].

Для ограничения порождения множества основных примеров предложен метод резолюций, разработанный Робинсоном [55].

Метод резолюций. Процедура поиска доказательства методом резолюций может применяться к любому множеству дизъюнктов с целью проверки его невыполнимости. Идея метода резолюций заключается в проверке наличия в множестве S пустого (ложного) дизъюнкта (противоречия). Если S содержит противоречие, то оно невыполнимо; если не содержит – то выводятся новые дизъюнкты до тех пор, пока не будет получено противоречие (это всегда имеет место для невыполнимого S). Подробнее метод резолюций см. в [9,66,55].

Недостатком метода резолюций является то, что неограниченное примене­ние правила резолюций может вызывать порождение большого числа дизъ­юнктов, многие из которых лишние и не относятся к делу, хотя и являются вполне корректными. Кроме того, для выполнимого множества дизъюнктов процедура, основанная на методе резолюций, будет продолжаться бесконечно.

Надо отметить, также, что методы резолюций неприемлемы в случае слож­ных проблем, так как пространство поиска, образуемое ими, возрастает экс­поненциально числу формул, используемых для описания проблемы.

Из-за указанных недостатков дедуктивные методы поиска решений не на­ходят в настоящее время широкого применения на практике и используются для проблемных областей с небольшим пространством поиска. Для более эф­фективного поиска решений необходимо использовать в системе эвристические знания о самом процессе решения задачи.

Методы повышения эффективности механизмов вывода, использующих эв­ристические процедуры при нахождении резольвент, а также новые стратегии резолюции описаны в [66]. Слабостью универсальных формальных дедуктив­ных систем является то, что они не в состоянии учитывать специфику конкрет­ных предметных областей. Поэтому другим направлением развития дедуктивных методов поиска решений явилась разработка планирующих систем и интеллектуальных решателей, ориентированных на проблемную область. Логиче­ский вывод в этих системах также преимущественно базируется на методе резолюций [63,124,22]. В этих системах производится аксиоматизация знаний о проблемной области и манипулирование ими при функционировании системы. Планирующие системы ориентированы преимущественно для нахождения це­лесообразного поведения интеллектуального робота.

Преимущества глубоко изученных логических моделей и дедуктивных ме­тодов (универсальность и определенность как формальной системы) послужи­ли основой разработки специальных логических языков высокого уровня, таких, как Пролог. Эти языки помогают структурировать дедуктивную проблему и обеспечивают различные встроенные функции, соединяются с характеризую­щими проблему формулировками и правилами эвристического руководства. Они определяют направление, которое использует вычислительная логика в попытке управлять сложными проблемами реального мира.