Вероятностный подход.
Случайная (или вероятностная) неопределенность может быть связана со случайностью событий, например, экономических ситуаций, состояний объекта, случайным характером отказов оборудования и другими факторами. При проектировании интеллектуальных СПР и организации работы с БЗ уровень достоверности и надежность многих знаний, фактов, событий и данных бывает различным. Для формализации рассуждений в условиях стохастической неопределенности используется теория вероятностей и статические решения. При реализации рассуждений с учетом неопределенности для вычисления вероятности некоторой гипотезы для варианта решения возможно применение байесовского подхода.
Рассмотрим основные положения байесовского метода и правило Байеса.
Пусть А есть событие в реальной действительности, а В – другое событие. Предположим, что события А и В не являются взаимно исключающими, но происходят условно при проявлении другого. Вероятность того, что событие А произойдет, если произойдет событие В, называется условной вероятностью.
Условная вероятность математически обозначается как Р(А|B), в которой вертикальная черта изображает «имело место», а полное выражение вероятности интерпретируется как «Условная вероятность того, что произойдет событие А при условии, что имело место событие В».
p(А|B)= 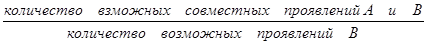 (6.1)
(6.1)
Количество возможных совместный проявлений А и В, или вероятность того, что А и В произойдут совместно, называется совместной вероятностью А и В.
Математически это представляется Р(АÇВ).
Количество способов возможного проявления В является вероятностью В, Р(В), и тогда
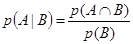 (6.2)
(6.2)
Так же, условная вероятность того, что произойдет событие В при условии, что имело место событие А определяется
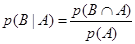 (6.3)
(6.3)
Отсюда,
p(ВÇА) =p(В|А)´p(А) (6.4)
Совместная вероятность является коммутативной, таким образом
p(АÇВ)= p(ВÇ А)
Следовательно
p(АÇВ) =p(В|А)´Р(А) (6.5)
Подстановка (6.5) в (6.2) приводит к следующему уравнению:
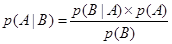 (6.6)
(6.6)
где
p(А|В) – условная вероятность того, что произойдет событие А при условии, что имело место событие В;
p(В|А) – условная вероятность того, что произойдет событие В при условии, что имело место событие А;
p(А) - вероятность того, что произойдет событие А;
p(В) - вероятность того, что произойдет событие В.
Уравнение (6.6) известно как правило (или формула) Байеса, которое названо именем Томаса Байеса, британского математика XVIII века, который предложил это правило.
Понятие условной вероятности предлагается, когда считается, что событие А было зависимым от события В. Этот принцип может быть расширен на случай, когда событие А зависит от некоторого числа несовместимых событий В1, В2, …, Вn.
Следующее множество уравнений может быть выведено из (6.2):
p(АÇВ1) =p(А|В1)´p(В1)
p(АÇВ2) =p(А|В2)´p(В2)
. . .
p(АÇВn) =p(А|Вn)´p(Вn)
Или после объединения.
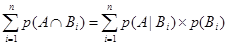 (6.7)
(6.7)
Если (6.7) просуммировано по всему полному перечню событий Bi, мы получаем
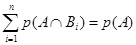 (6.8)
(6.8)
Это приводит к следующему уравнению условной вероятности, т.е. Р(А) выражается с помощью формулы полной вероятности:
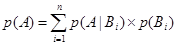 (6.9)
(6.9)
Если проявление события А зависит только от двух взаимно исключающих событий, например В и НЕ В, тогда (6.9) будет выглядеть так:
p(А)=p(А|B)´p(B)+p(A\ØB)´p(ØB) (6.10)
Где Ø - логическое НЕ.
Также
p(В)=p(В|А)´p(А)+p(В\ØА)´p(ØА) (6.11)
Подставим теперь (6.11) в формулу Байеса (6.6), что приводит к
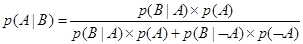 (6.12)
(6.12)
Уравнение (6.12) обеспечивает основу использования теории вероятности для управления неопределенностью в интеллектуальных системах.
Байесовский вывод.
Используя уравнение (6.12) мы можем теперь от теории вероятностей обратить наше внимание вновь к интеллектуальным системам [115]. Допустим все правила в БЗ представлены в следующей форме:
Если Н истинно
Тогда С истинно {с вероятностью р}.
Это правило подразумевает, что если событие Н происходит, тогда вероятность, что событие С произойдет р.
Что будет, если событие С произошло, но мы не знаем, произошло ли событие Н? Рассмотрим возможность вычисления вероятности того, что событие Н также произошло.
Уравнение (6.12) позволяет нам это сделать. Мы просто используем Н и С вместо А и В. В интеллектуальных системах Н обычно обозначает гипотезы, а С – свидетельства в поддержку этих гипотез.
Таким образом, уравнение (6.12), выраженное в терминах гипотез и свидетельств, выглядит так
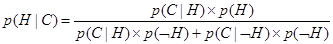 (6.13)
(6.13)
p(Н) – априорная (безусловная) вероятность того, что гипотеза Н является истинной;
p(С|Н) – вероятность того, что гипотеза Н является истинной, будет результатом свидетельства С;
p(ØН) - априорная (безусловная) вероятность того, что гипотеза Н является ложной;
p(С|ØН) – вероятность нахождения свидетельства С даже когда гипотеза Н ложна.
Уравнение (6.13) предполагает, что вероятность гипотезы Н, p(Н) должна быть определена перед тем, как проверены какие-либо свидетельства.
В интеллектуальных СПР вероятности требуются для решения задачи, которые ставят эксперты. Эксперт определяет априорные вероятности для возможной гипотезы p(Н) и p(ØН), а также условные вероятности для наблюдаемого свидетельства С, если гипотеза Н истинна, p(С|Н), и если гипотеза Н ложна, p(С|ØН). Пользователи обеспечивают информацию о наблюдаемом свидетельстве и интеллектуальная система вычисляет p(С|Н) для гипотезы Н в свете представленного пользователем свидетельства С. Вероятность p(С|Н) называется апостериорной вероятностью гипотезы Н при наблюдаемом свидетельстве С.
Рассмотрим ситуации, когда эксперт, основываясь на простом свидетельстве С, не может выбрать простую гипотезу, но скорее обеспечивает многочисленные гипотезы Н1, Н2,…, Нт. Или когда имеются многочисленные свидетельства С1, С2, …, Сn и эксперт также выдает множество гипотез.
Мы можем обобщить уравнение (6.13) принимая во внимание и многочисленные гипотезы Н1, Н2, …, Нт и многочисленные свидетельства С1, С2, …, Сn. Но гипотезы, так же как и свидетельства должны быть взаимно исключающими.
Для простого свидетельства С и многочисленных гипотез Н1, Н2, …, Нт следует:
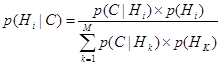 (6.14)
(6.14)
Для многочисленных свидетельств С1, С2, …, Сn и многочисленных гипотез Н1, Н2, …, Нт следует:
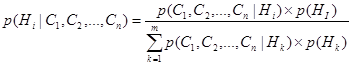 (6.15)
(6.15)
Применение уравнения (6.15) требует получения условных вероятностей всех возможных комбинаций свидетельств для всех гипотез. Это требование ложится огромным грузом на эксперта и делает его задачу практически невыполнимой.
Поэтому в интеллектуальных СПР и ЭС, тонкости совместного влияния многочисленных свидетельств должны не учитываться, а допускаться условная независимость между различными свидетельствами.
Следовательно, вместо неосуществимого уравнения (6.15) мы получаем
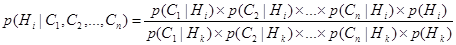 (6.16)
(6.16)
Для того, чтобы прояснить, каким образом интеллектуальная система вычисляет все апостериорные вероятности и в итоге ранжирует потенциально истинную гипотезу, рассмотрим простой пример.
Предположим, что эксперт, имея три условно независимых свидетельства С1, С2 и С3, создает три взаимно исключающие гипотезы Н1, Н2 и Н3 и обеспечивает априорные вероятности для этих гипотез – p(Н1), p(Н2) и p(Н3) соответственно. Эксперт также определяет условные вероятности каждого отмеченного свидетельства для всех возможных гипотез.
В Таблице 6.1. показаны априорные и условные вероятности, обеспеченные экспертом.
Таблица 6.1.
Априорные и условные вероятности.
| Вероятности | Гипотезы | ||
| i=1 | i=2 | i=3 | |
| P(Hi) P(C1|Hi) P(C2|Hi) P(C3|Hi) | 0.4 0.3 0.9 0.6 | 0.35 0.8 0.0 0.7 | 0.25 0.5 0.7 0.9 |
Допустим, что мы сначала наблюдаем свидетельство С3. Интеллектуальная система вычисляет апостериорные вероятности для всех гипотез по уравнению (6.14):
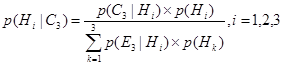
Таким образом
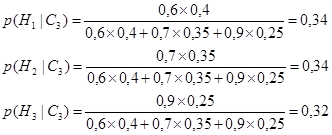
Как можно видеть, после того, как наблюдается свидетельства С3, доверие гипотезе Н2 и становится равным доверию гипотезе Н1. Доверие гипотезе Н3 также возрастает и даже приблизительно достигает доверию гипотезам Н1 и Н2.
Предположим теперь, что мы наблюдаем свидетельство С1. Апостериорные вероятности рассчитываются по уравнению (6.16):
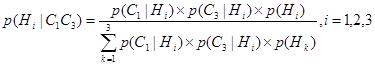
Таким образом
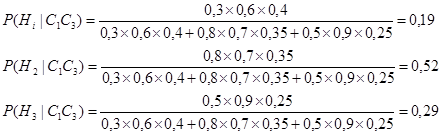
Гипотеза Н2 теперь рассматривается как наиболее вероятная, т.к. доверие гипотезе резко уменьшается.
После наблюдения свидетельства С2 интеллектуальная СПР также вычисляет последние апостериорные вероятности для всех гипотез:
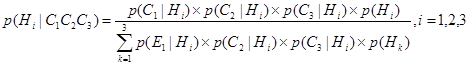
Таким образом
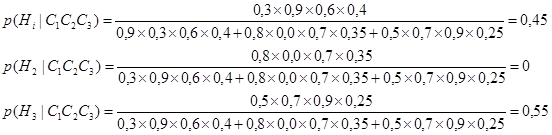
Хотя первоначальное ранжирование, предложенное экспертом было Н1, Н2 и Н3, только гипотезы Н1 и Н3 остались для рассмотрения после всех свидетельств (С1, С2 и С3), которые наблюдались. Гипотеза Н2 теперь может быть полностью исключена.
Заметим, что гипотеза Н3 теперь рассматривается как более предпочтительная, чем гипотеза Н1.
При применении методов на базе байесовской логики возникают трудности с получением большого числа данных, необходимых для определения условных вероятностей.
На практике делается предположение о независимости наблюдений, что видимо влияет на строгость статической модели. Подобные допущения присутствуют в методе на базе байесовского подхода, предложенного в [85].
Дуда, Харт и Нильсон видоизменили формулы Байеса для выводов в инженерии знаний и предположили метод выводов, названный субъектным байесовским методом.
Основные цели этого метода были успешно реализованы ими в экспертной системе PROSPECTOR [84].
Дата добавления: 2017-02-20; просмотров: 730;
