Композиционное правило вывода.

Пусть U и V – два универсальных множества с базовыми переменными u и v соответственно. Пусть R(u), R(u,v) и R(v) обозначают ограничения на u, (u,v) и v соответственно и представляют собой нечеткие отношения в U, U´V и V.

Пусть A и F – нечеткие подмножества множеств U и U´V. Тогда композиционное правило вывода утверждает, что решение уравнений назначения

R(u)=A (унарное нечеткое отношение) (6.27)

R(u,v)=F (бинарное нечеткое отношение) (6.28)

Имеет вид (v)=A°F (6.29)

Где A°F – композиция A и F. В этом смысле мы должны делать вывод. R(v)= A°F из того, что R(u)=A и R(u,v)=F.

При этом функция принадлежности определяется как

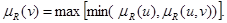(6.30)

Для определения композиционного правила вывода применяю нечеткие отношения. Известно достаточно большое количество нечетких отношений, используемых в композиционных правилах вывода.

Например, нечеткое отношение Заде:

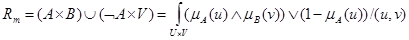(6.31)

В качестве простой иллюстрации этого правила предположим, что

U=V=1+2+3+4

A=малый=1/1+0.6/2+0./3

F=примерно равны=1/(1,1)+1/(2,2)+1/(3,3)+1/(4,4)+0,5/((1,2)+(2,1)+(2,3)+(3,2)+(3,4)+(4,3)).

Другими словами, А-унарное нечеткое отношение в U, названное «малый»; F – бинарное нечеткое отношение в U´V, названное «примерно равны».

Уравнения назначения в этом случае имеют вид:

R(u)=малый

R(u,v)=примерно равны,

И следовательно

R(v)=малый°примерно равны=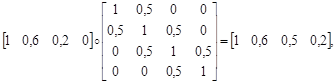

Что можно аппроксимировать следующим образом:

R(v)=более или менее малый.

Примечание 1: уравнение назначения для X имеет вид x=u:R(x) или эквивалентно x=u, uÎR(X), и отражает то, что элементу х назначается значение u с учетом ограничения R(X).

Итак, используя композиционное правило вывода, из того, что R(u)=малый и R(u,v)= примерно равны, мы вывели, что

R(v)=[1 0.6 0.5 0.2] точно

и R(v)= «более или менее малый» - в качестве лингвистического приближения.

Словами это приближенный вывод можно записать в виде:

u-«малый» (предпосылка)

u и v – «примерно равны» (предпосылка)

v – «более или менее малый» (приближенный вывод)

Основная идея этого схематически описанного метода состоит в следующем. Каждый факт или предпосылка записывается в виде уравнений назначения в отношениях, содержащих одно или больше число ограничений на базовые переменные. Эти уравнения решаются относительно желаемых ограничений при помощи композиции нечетких отношений. Получаемые решения и представляют собой вывод из данного набора предпосылок.

Рассмотрим пример применения приближенных рассуждений и композиционного правила вывода в управлении производственным процессом.