Приближенные рассуждения.
В классической теории исчисления высказываний выражение «Если А, Тогда В», где А и В – пропозициональные переменные (пропозициональная переменная – это переменная для предложений, которые рассматриваются лишь с точки зрения их истинности или ложности), записывается как А®В, где импликация (®) рассматривается как связка, смысл которой определяется таблицей истинности.
Таким образом А®ВºØАÚВ (6.17)
В том смысле, что А®В (А влечет В) и ØАÚВ (не А или В) имеют идентичные таблицы истинности. Более важным в нашем случае является неопределенное высказывание «Если А, Тогда В», коротко А®В, в котором А (антецедент) и В (консеквент) – нечеткие множества, а не пропозициональные переменные («пропозиция» означает предложение, выражение, высказывание).
Типичные примеры высказываний:
Если «большой», Тогда «малый»
Если «скользкий», Тогда «опасный;»
Они являются сокращениями предложений:
Если х-«большой», Тогда у-«малый»;
Если дорога «скользкая», Тогда езда «опасна».
В сущности предложения этого вида описывают отношения между двумя неопределенными переменными. Это означает что неопределенное высказывание следует скорее определить как нечеткое отношение в смысле (5.25), а не как связку в смысле (6.17).
Здесь целесообразно определить сначала декартово произведение двух нечетких множеств.
Пусть А-нечеткое подмножество области рассуждений U и пусть В- нечеткое подмножество другой области рассуждений V. Тогда декартово произведение А и В, обозначаемое А´В, определяется следующим образом
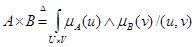(6.18)
где U´V означает декартово произведение множеств U и V, т.е.
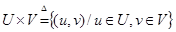
Заметим, что когда А и В – не нечеткие, (6.18) преобразовывается в обычное определение декартова произведения множеств.
Иными словами, (6.18) означает, что А´В нечеткое множество упорядоченных пар (u,v),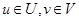 
, со степенью принадлежности (u,v) к (А´В), задаваемой формулой 
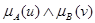. В этом смысле А´В есть нечеткое отношение U и V.
Пример 6.1. Пусть
U=1+2 (6.19)
V=1+2+3 (6.20)
A=1/1+0,8/2 (6.21)
B=0,6/1+0,9/2+1/3 (6.22)
Тогда
А´В=0,6/(1,1)+0,9/(1,2)+1/(1,3)+0,6/(2,1)+0,8/(2,2)+0,8/(2,3) (6.23)
Отношение, определенное в (6.17) можно представить матрицей отношения
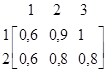
Смысл нечеткого высказывания вида «Если А, Тогда В» становится ясен, если рассматривать его как специальный случай условного высказывания «Если А, Тогда В, Иначе С», где А, В и С – нечеткие подмножества, возможно, различных областей U и V, соответственно.
В терминах декартова произведения последнее предложение определяется так:
Если А, Тогда В, Иначе С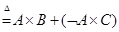 
(6.25)
Где + означает объединение нечетких множеств А´В и (ØА´С).
Чтобы обобщить понятие материальной импликации на нечеткие множества, предположим, что U и V – два возможно различных универсальных множества, а А, В и С – нечеткие подмножества множеств U, V и V соответственно.
Сначала определим смысл высказывания
Если А, Тогда В, Иначе С, и затем определим
Если А, Тогда В как частный случай высказывания Если А, Тогда В, Иначе С.
Определение. Высказывание Если А, Тогда В, Иначе С есть бинарное нечеткое отношение в U´V, определяемое следующим образом:
Если А, Тогда В, Иначе С=А´В+ØА´С (6.26)
То есть, если А,В и С – унарные нечеткие отношения в U, V и V, тогда Если А, Тогда В, Иначе С – бинарное нечеткое отношение в U´V, которое является объединением декартова произведения А и В (см.(5.23)) и декартова произведения отрицания А и С.
Далее высказывание Если А, Тогда В можно рассматривать как частный случай высказывания Если А, Тогда В, Иначе С при допущении, что С – полное множество V.
Т.о. Если А, Тогда В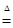 
Если А, Тогда В, Иначе V=А´В+ØА´V (6.27)
В сущности это равнозначно интерпретации высказывания Если А, Тогда В высказыванием Если А, Тогда В, Иначе безразлично.
Пример 6.2. Иллюстрация (6.26) и (6.27)
Предположим, что
U=V=1+2+3
А=малый=1/1+0,4/2
В=большой=0,4/2+1/3
С=не большой=1/1+0,6/2
Тогда Если А, Тогда В, Иначе С=(1/1+0,4/2)´( 0,4/2+1/3)+(0,6/2+1/3)´ (1/1+0,6/2)=0,4/(1,2)+1/(1,3)+0,6/(2,1)+0,6/(2,2)+0,4/(2,3)+1/(3,1)+0,6/(3,2)
Что можно представить в виде матрицы отношения
Если А, Тогда В, Иначе С=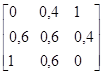 
Аналогично
Если А, Тогда В=(1/1+0,4/2)´(0,4/2+1/3)+(0,6/2+1/3)´(1/1+1/2+1/3) =0,4/(1,2)+1/(1,3)+0,6/(2,1)+0,6/(2,2)+0,6/(2,3)+1/(3,1)+1/(3,2)+1/(3,3)
Или эквивалентно
Если А, Тогда В=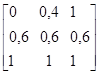 
Дата добавления: 2017-02-20; просмотров: 418;