Корни характеристического уравнения и решение для свободной функции
Если цепь описывается уравнением второго порядка, свободная составляющая содержит два слагаемых:
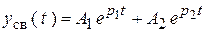 (1).
(1).
где 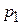 и
и 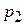 - корни квадратного характеристического уравнения.
- корни квадратного характеристического уравнения.
Они могут быть :
− действительными различными числами;
− действительными равными числами;
− комплексно-сопряженными числами.
Во всех случаях действительные компоненты – отрицательные.
Корни характеристического уравнения определяют характер переходного процесса (форму переходной функции). Поэтому уравнение и называют характеристическим. Т.о. возможны три варианта:
1. Решение (1) является универсальным, но непосредственно срабатывает только при действительных различных корнях.
2. При действительных равных корнях отыскание решения в форме (1) в каждом конкретном случае приведет к неопределенности вида 0/0. После раскрытия ее по правилу Лапиталя получается конкретный результат, который можно получить сразу, отыскивая решение в виде:
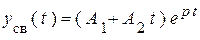 (2).
(2).
3. Используя формулу (1) при комплексно-сопряженных корнях мы получим два комплексно-сопряженных слагаемых, которые сворачиваются по формулам Эйлера и образуют обязательно действительную функцию. К тому же результату можно прийти, если отыскивать решение в виде:
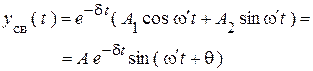 (3).
(3).
Здесь: 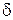 и
и 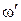 − компоненты корней характеристического уравнения:
− компоненты корней характеристического уравнения: 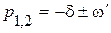 .
.
Во всех приведенных решениях есть две постоянные интегрирования: 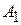 и
и 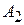 или
или 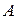 и
и 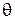 .
.
 Рис. 1.63
Рис. 1.63
|
 Рис. 1.62.
Рис. 1.62.
|
4. Возможен нулевой корень, который дает в решении постоянную свободную составляющую (ток в индуктивном контуре без потерь (рис 1.62), напряжение на последовательно соединенных емкостях (рис. 1.63).
5. Два мнимых сопряженных корня дают незатухающую свободную синусоиду (свободные колебания в идеальном колебательном контуре).
Дата добавления: 2018-09-24; просмотров: 1039;
