Разряд конденсатора на сопротивление
И индуктивность
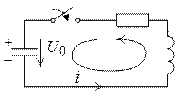 Рис. 1.84
Рис. 1.84
|
Конденсатор 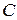 , предварительно заряженный от постороннего источника до напряжения
, предварительно заряженный от постороннего источника до напряжения 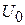 , разряжается после коммутации на сопротивление
, разряжается после коммутации на сопротивление 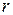 и индуктивность
и индуктивность 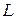 (Рис. 1.84). Внешних источников уже нет. Это свободный процесс. Наблюдается, пока накопленная до коммутации энергия
(Рис. 1.84). Внешних источников уже нет. Это свободный процесс. Наблюдается, пока накопленная до коммутации энергия 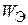 не израсходуется на тепловые потери в сопротивлении
не израсходуется на тепловые потери в сопротивлении 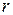 .
.
На этом простейшем примере одноконтурной схемы рассматривается характер свободного процесса в цепи второго порядка.
СУР: 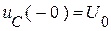 ;
; 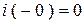 .
.
ННУ: 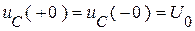 ;
; 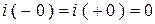 .
.
ЗНУ: 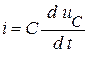 ;
; 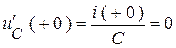 .
.
НУР: 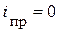 ;
; 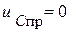 .
.
Уравнение цепи для функции 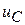 :
:
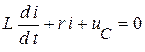 ,
,
т.к.:
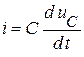 ,
, 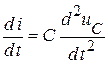 ,
,
получим:
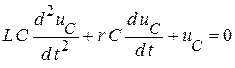 ,
,
или
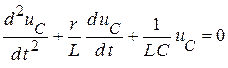 .
.
Уравнение однородное, описывает только свободный процесс. Значит, уравнение для тока 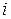 имеет точно такой же вид.
имеет точно такой же вид.
Характеристическое уравнение цепи и его корни:
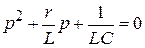 .
.
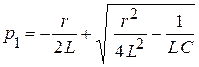 ;
;
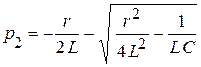 .
.
В зависимости от значений корней характеристического уравнения 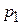 и
и 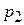 различают три характера переходного процесса:
различают три характера переходного процесса:
1. Апериодический процесс:
Корни 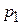 и
и 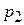 различные действительные отрицательные числа, что соответствует соотношению параметров (дискриминант больше нуля).
различные действительные отрицательные числа, что соответствует соотношению параметров (дискриминант больше нуля).
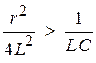 →
→ 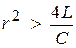 →
→ 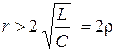 ,
,
где 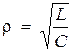 − волновое характеристическое сопротивление контура.
− волновое характеристическое сопротивление контура.
Решение однородного уравнения и производная от этого решения:
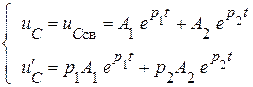 .
.
Определение постоянных интегрирования по начальным условиям из системы алгебраических уравнений:
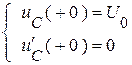 →
→ 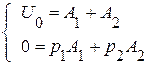 .
.
Решая систему, получили:
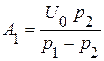 и
и 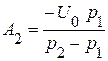 .
.
Запишем окончательные решения для напряжения 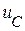 и других функций с учетом рассчитанных
и других функций с учетом рассчитанных 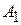 и
и 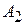 :
:
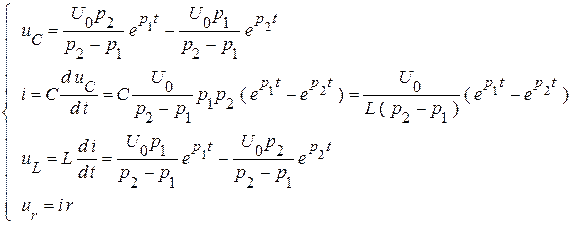
Функции тока 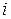 и напряжения
и напряжения 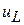 записаны по дифференциальным соотношениям. В решении для тока
записаны по дифференциальным соотношениям. В решении для тока 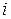 произведение корней квадратного уравнения по теореме Виета равно свободному члену
произведение корней квадратного уравнения по теореме Виета равно свободному члену 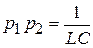 .
.
Построение переходных функций:
Из анализа решений для корней характеристического уравнения 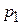 и
и 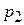 имеет что:
имеет что:
1.) 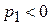 ; 2.)
; 2.) 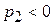 ; 3.)
; 3.) 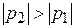 ; 4.)
; 4.) 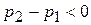 .
.
С учетом этого, сопоставим характеристики слагаемых 1 и 2 в решениях:
Для напряжения 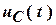 : :
| |
| 1сл. > 0 | 2сл. < 0 |
| | 1сл.( + 0 ) | > | 2сл.( + 0 ) | | |
| 1сл. затухает медленно | 2сл. затухает быстро |
| Сумма двух экспонент разного знака с разными постоянными времени дает кривую с максимумом второго порядка и точкой перегиба. | |
Для тока 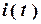 : :
| |
| 1сл. < 0 | 2сл. > 0 |
| | 1сл.( + 0 ) | = | 2сл.( + 0 ) | | |
| 1сл. затухает медленно | 2сл. затухает быстро |
Для напряжения 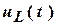 : :
| |
| 1сл. > 0 | 2сл. < 0 |
| | 1сл.( + 0 )| < | 2сл.( + 0 ) | | |
| 1сл. затухает медленно | 2сл. затухает быстро |
 Рис. 1.85
Рис. 1.85
|
Анализ решения:
1. Процесс называется апериодическим, т.к. функции тока 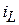 и напряжения
и напряжения 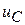 , подчиняющиеся законам коммутации, не меняют знака.
, подчиняющиеся законам коммутации, не меняют знака.
2. Во время переходного процесса ток отрицательный вследствие того, что конденсатор разряжается, а условные направления напряжения 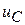 и тока
и тока 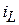 приняты одинаковые.
приняты одинаковые.
3. Напряжение 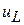 меняет знак. ПротивоЭДС по принципу Ленца сначала препятствует нарастанию тока, а затем препятствует его уменьшению, значит, меняет свое направление.
меняет знак. ПротивоЭДС по принципу Ленца сначала препятствует нарастанию тока, а затем препятствует его уменьшению, значит, меняет свое направление.
4. Энергетика процесса.
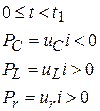
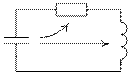 Рис. 1.86
Рис. 1.86
| 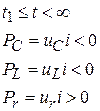
 Рис. 1.87
Рис. 1.87
|
Знак мгновенной мощности 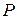 определяет направление потоков энергии. Они отмечены стрелками на рис. 1.86 и на рис. 1.87. При
определяет направление потоков энергии. Они отмечены стрелками на рис. 1.86 и на рис. 1.87. При 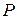 >0 энергия воспринимается элементами схемы. При
>0 энергия воспринимается элементами схемы. При 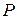 <0 – отдается им.
<0 – отдается им.
2. Предельный апериодический процесс:
При соотношении: 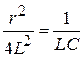 ,
, 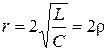 , корни действительные равные отрицательные числа.
, корни действительные равные отрицательные числа.
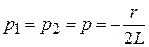
Решение для напряжения 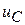 и его производной
и его производной 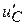 :
:
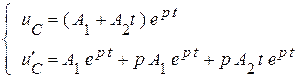
Определение постоянных по начальным условиям:
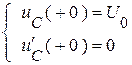
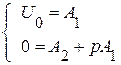 →
→ 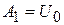 и
и 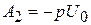 .
.
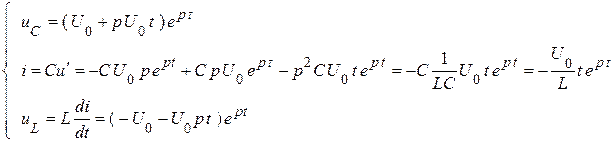
Математическая форма решения изменилась, но процесс сохранил свой характер, остался апериодическим.
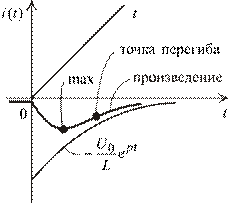 Рис. 1.88
Рис. 1.88
|
Построим, например ток 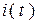 (рис. 1.88). Форма кривой осталась прежней, но получена как результат перемножения изображенных на рисунке сомножителей.
(рис. 1.88). Форма кривой осталась прежней, но получена как результат перемножения изображенных на рисунке сомножителей.
Таким образом сохраняется та же форма кривых для напряжений: 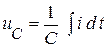 и
и 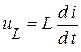 . Но стоит перешагнуть норму
. Но стоит перешагнуть норму 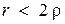 , как характер процесса изменится.
, как характер процесса изменится.
3. Колебательный процесс:
При соотношении параметров 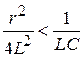 , когда
, когда 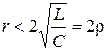
корни характеристического уравнения комплексно-сопряженные:
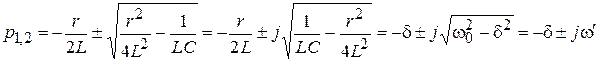 .
.
Компоненты корней
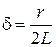 – коэффициент затухания;
– коэффициент затухания;
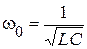 – частота собственных незатухающих колебаний;
– частота собственных незатухающих колебаний;
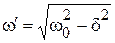 – частота свободных затухающих колебаний.
– частота свободных затухающих колебаний.
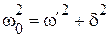
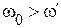
Решение для напряжения 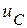 и его производная
и его производная 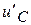 .
.
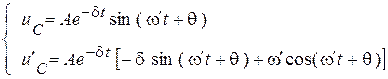
Сложение синусоид в комплексной плоскости (рис. 1.89):
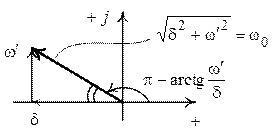 Рис. 1.89
Рис. 1.89
|
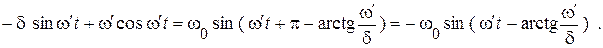
Подставим результат сложения в решение для 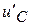 , учитывая теперь начальную фазу:
, учитывая теперь начальную фазу:
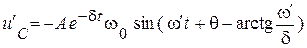 .
.
Определение постоянных из начальных условий:
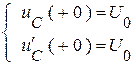
После их подстановки в решения, получим систему:
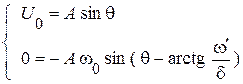
Решаем систему:
В последнем уравнении нулевым может быть только второй сомножитель, т.е. 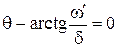 , откуда
, откуда 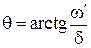 .
.
Тогда: 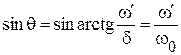 (см. рис. 1.89),
(см. рис. 1.89), 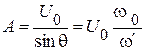 .
.
Искомые функции:
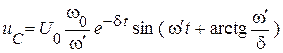 ,
,
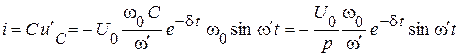 ,
,
Здесь и в последующем решении учитывается, что 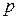 есть волновое (характеристическое) сопротивление последовательного rLC контура:
есть волновое (характеристическое) сопротивление последовательного rLC контура:
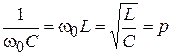
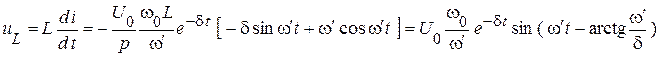
Здесь также используется полученный выше результат сложения синусоид.
Итак, перепишем еще раз решения для свободных функций, записанных с использованием вторичных параметров.
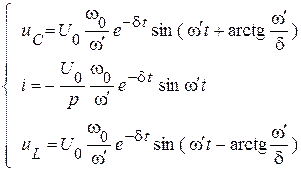
Частный случай контура без потерь.
Компоненты вторичных параметров:
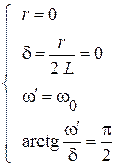 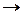
| Переходные функции:
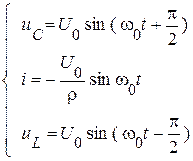
|
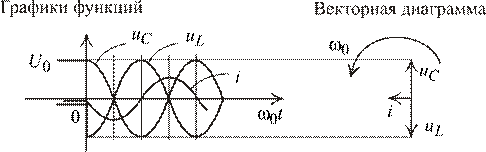 Рис. 1.90
Рис. 1.90
|
Сразу после коммутации наблюдаем новый установившийся режим синусоидального тока. Свободные незатухающие колебания с частотой 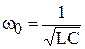 . Как при резонансе напряжений в LC контуре без потерь. Фазовая ориентация обычная для синусоидального режима. На рис. 1.90 показана векторная диаграмма мгновенных значений. Векторы напряжений
. Как при резонансе напряжений в LC контуре без потерь. Фазовая ориентация обычная для синусоидального режима. На рис. 1.90 показана векторная диаграмма мгновенных значений. Векторы напряжений 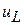 и
и 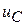 проектируются в амплитуды синусоид при
проектируются в амплитуды синусоид при 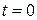 . Период определяется по формуле Томпсона:
. Период определяется по формуле Томпсона: 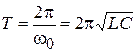 .
.
Графики затухающих колебаний.
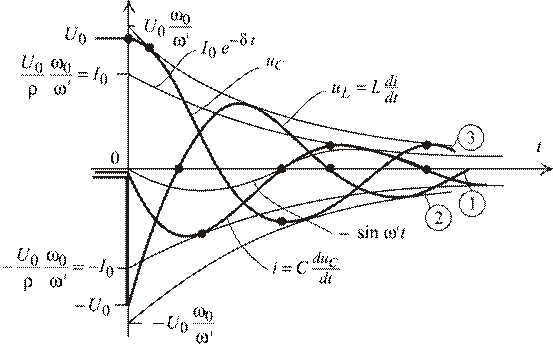 Рис. 1.91
Рис. 1.91
|
Сначала строится ток 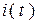 , как затухающая синусоида, вписанная в экспоненциальный коридор (произведение незатухающей синусоиды и экспоненты). Потом напряжение
, как затухающая синусоида, вписанная в экспоненциальный коридор (произведение незатухающей синусоиды и экспоненты). Потом напряжение 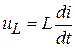 . Затем напряжение
. Затем напряжение 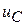 вписываем в тот же коридор, что и
вписываем в тот же коридор, что и 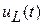 , так чтобы
, так чтобы 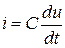 . Максимумы затухающих синусоид находятся левее точек касания с экспонентами и не совпадают по времени с максимумом синусоидального сомножителя.
. Максимумы затухающих синусоид находятся левее точек касания с экспонентами и не совпадают по времени с максимумом синусоидального сомножителя.
Деформация характера.
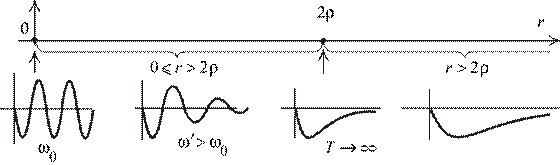 Рис. 1.92
Рис. 1.92
|
При 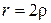 ,
, 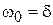 ,
, 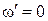 и
и 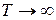 процесс переходит в апериодический. Значения
процесс переходит в апериодический. Значения 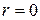 и
и 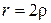 являются границами нормы, где при накоплении
являются границами нормы, где при накоплении 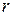 процесс приобретает новое качество.
процесс приобретает новое качество.
Наложение свободного и принужденного процесса.
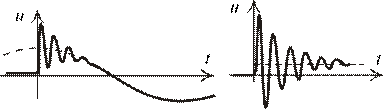 Рис. 1.93
Рис. 1.93
|
Задача. Цепь с синусоидальным источником ЭДС (рис. 1.94). Наложение принужденных и свободных составляющих.
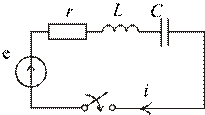 Рис. 1.94
Рис. 1.94
|
Условие:
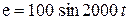 (В);
(В); 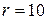 (Ом);
(Ом);
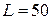 (мГн);
(мГн); 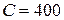 (мкФ).
(мкФ).
Определить закон изменения тока 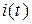 .
.
Решение:
1. Рассмотрим СУР.
Источник отключен: 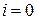 ;
; 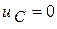 .
.
В конце СУР: 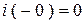 ;
; 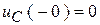 .
.
2. Зафиксируем ННУ: 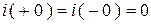 ;
; 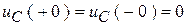 .
.
3. Определим ЗНУ: 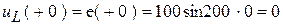 .
.
Т.к. 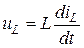 , то
, то 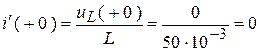 .
.
4. Рассчитаем НУР синусоидального тока, принужденную составляющую искомой функции и значение ее первой производной:
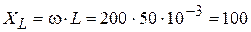 ;
;
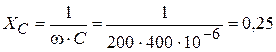 .
.
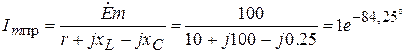 ,
,
Принужденная составляющая искомой функции:
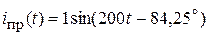 .
.
Начальное значение принужденной составляющей:
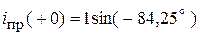 .
.
Первая производная принужденной составляющей искомой функции:
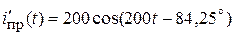 .
.
Начальное значение производной принужденной составляющей:
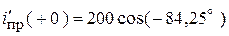 .
.
5. Составим характеристическое уравнение и найдем его корень:
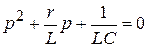 ;
;
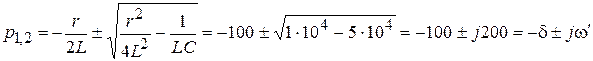 .
.
здесь:
коэффициент затухания 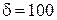 , постоянная времени
, постоянная времени 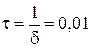 (с), угловая частота
(с), угловая частота 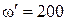 , период свободной составляющей
, период свободной составляющей 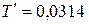 (с).
(с).
6. Запишем общее решение в виде:
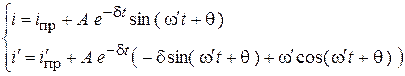
7. Определим постоянную интегрирования и искомую функцию:
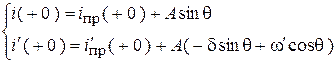
или 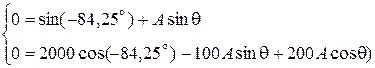
Решая совместно два уравнения, получаем: 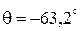 и
и 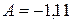 .
.
Следовательно, ток 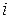 равен:
равен:
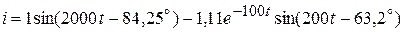 .
.
9. Построит графики для найденной функции (рис. 1.95):
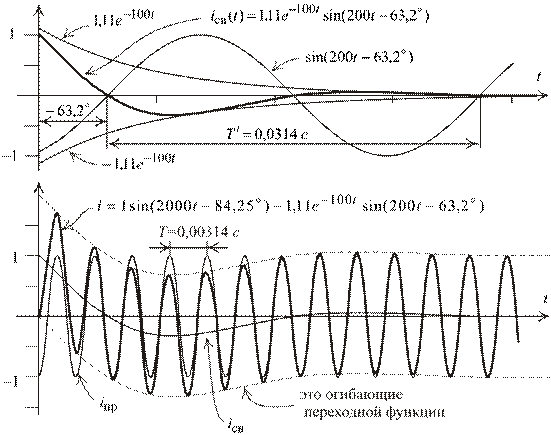 Рис. 1.95
Рис. 1.95
|
Дата добавления: 2018-09-24; просмотров: 983;
