Примеры решения задач в цепи
Первого порядка.
Задача 1. Цепь с постоянным источником ЭДС (рис.1.33).
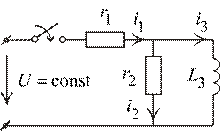 Рис. 1.33
Рис. 1.33
|
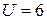 ( В );
( В ); 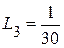 ( Г );
( Г );
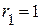 ( Ом );
( Ом ); 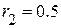 ( Ом ).
( Ом ).
Определить мгновенные значения токов, напряжение на катушке и сопротивлении 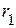 .
.
Решение:
1. Рассмотрим СУР.
Источник отключен: 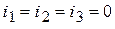 ;
; 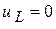 .
.
В конце СУР: 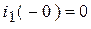 ;
; 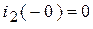 ;
; 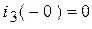 ;
; 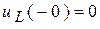 .
.
2. Зафиксируем ННУ: 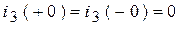 .
.
3. Определим ЗНУ: по первому закону коммутации индуктивность разрывает ветвь в расчетной схеме для 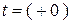 (рис. 1.34):
(рис. 1.34):
 Рис. 1.34
Рис. 1.34
|
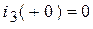 ;
;
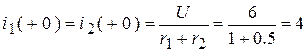 ;
;
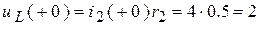
4. Рассчитаем НУР постоянного тока (рис. 1.35):
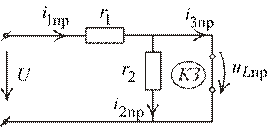 Рис. 1.35
Рис. 1.35
|
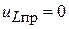 как напряжение короткого замыкания;
как напряжение короткого замыкания;
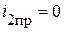 ;
;
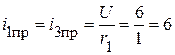 ;
;
Начальные значения принужденных составляющих − те же самые величины 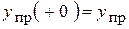 .
.
5. Составим характеристическое уравнение и найдем его корень:
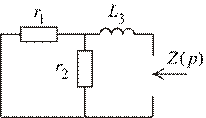 Рис. 1.36
Рис. 1.36
|
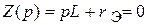 ;
;
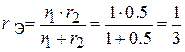 ;
;
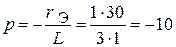 .
.
Постоянная времени и длительность переходного процесса равна:
 (с),
(с), 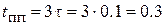 (с).
(с).
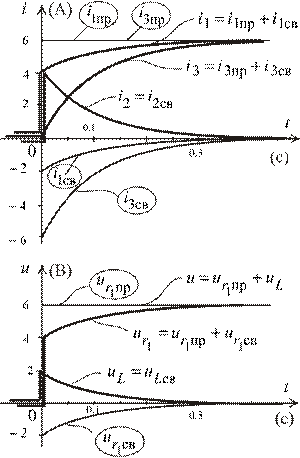 Рис. 1.37
Рис. 1.37
|
6. Определим постоянные интегрирования:
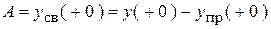 .
.
7. Запишем общее решение в виде:
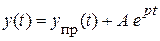 .
.
Расчет сведем в таблицу:
| СУР | НУ | НУР | ПИ | ПФ | |
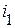
| -2 | 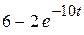
| |||
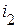
| 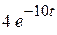
| ||||
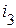
| -6 | 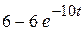
| |||
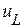
| 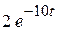
|
Определим напряжение
на сопротивлении 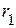 :
:
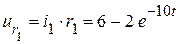 .
.
8. Построим графики рассматриваемых функций (рис. 1.37)
Задача 2. Переходный процесс в цепи с постоянным источником ЭДС при изменении параметров схемы (рис. 1.38).
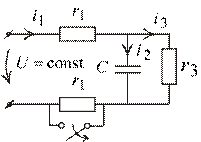 Рис. 1.38
Рис. 1.38
|
Условие:
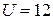 ( В );
( В ); 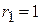 ( Ом );
( Ом ); 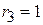 ( Ом ),
( Ом ), 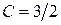 ( мкФ ).
( мкФ ).
Определить функции изменения токов
и напряжения на конденсаторе.
Решение:
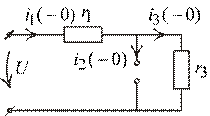 Рис. 1.39
Рис. 1.39
|
1. Рассмотрим СУР постоянного тока и конечные значения функций.
Нижнее сопротивление 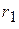 шунтировано ключом, емкость разрывает цепь постоянного тока.
шунтировано ключом, емкость разрывает цепь постоянного тока.
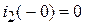 ;
;
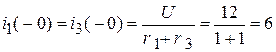 ;
;
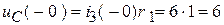 .
.
2. Зафиксируем ННУ: 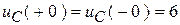 .
.
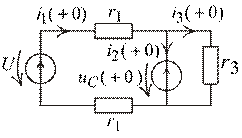 Рис. 1.40
Рис. 1.40
|
3. Определим ЗНУ по схеме замещения для 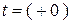 (рис. 1.40).
(рис. 1.40).
Система уравнений не связана, и каждое решение находится для отдельно взятого уравнения:
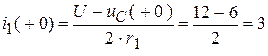 ;
;
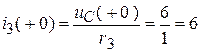 ;
; 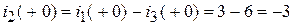 .
.
4. Рассчитаем НУР постоянного тока (рис. 1.41):
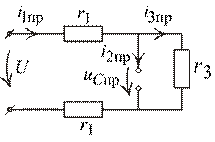 Рис. 1.41
Рис. 1.41
|
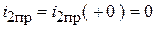
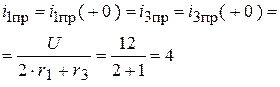 ;
;
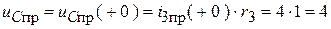 .
.
5. Составим характеристическое уравнение и найдем его корень (рис.1. 42):
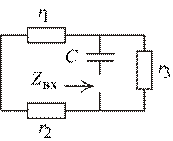 Рис. 1.42
Рис. 1.42
|
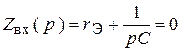 ;
; 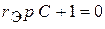 ;
; 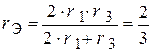 .
.
Решая уравнение, нашли: 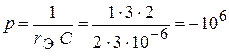 ,
,
Постоянная времени и длительность переходного процесса равна:
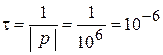 ( с ),
( с ), 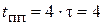 ( мс ).
( мс ).
6. Определим постоянные интегрирования:
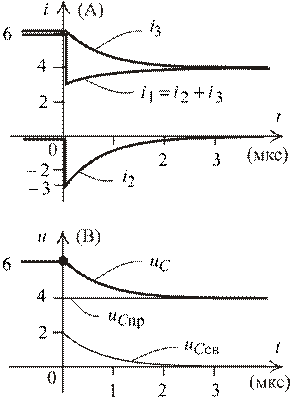 Рис. 1.43
Рис. 1.43
|
В общем виде:
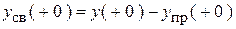 .
.
Для конкретных функций:
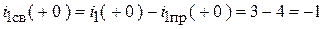 ;
;
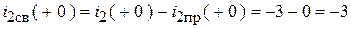
 .
.
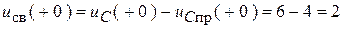 .
.
7. Переменные функции:
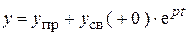 .
.
Решение сведем в таблицу:
| СУР | НУ | НУР | ПИ | ПФ | |
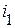
| −1 | 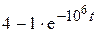
| |||
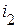
| −3 | 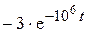
| |||
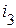
| 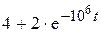
| ||||
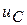
| 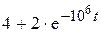
|
8. Обратим внимание на начальную скорость изменения нарастания напряжения 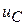 .
.
Если 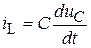 , то
, то 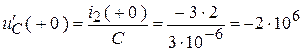 .
.
Значит, скоротечны электромагнитные переходные процессы.
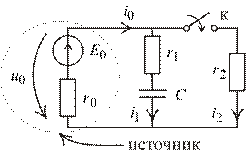 Рис. 1.44
Рис. 1.44
|
Задача 3. Цепь первого порядка со схемой замещения реального постоянного источника напряжения. Анализ работы источника по его вольтамперной характеристике (рис. 1.44).
Условие:
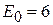 ( В );
( В ); 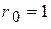 ( Ом );
( Ом ); 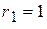 ( Ом );
( Ом ); 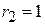 ( Ом );
( Ом ); 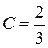 ( мкФ ).
( мкФ ).
Рассчитать все переходные функции.
Решение:
1. Рассмотрим СУР постоянного тока и конечные значения функций. Ключ «К» разомкнут, емкость не пропускает постоянный ток: 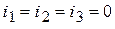 ;
; 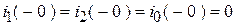 ;
;  .
.
2. Зафиксируем ННУ: 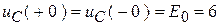 .
.
3. Определим ЗНУ по схеме замещения для 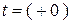 методом узловых потенциалов (рис. 1.45).
методом узловых потенциалов (рис. 1.45).
 Рис. 1.45
Рис. 1.45
|
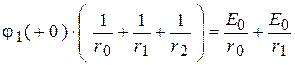 ,
,
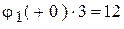 →
→ 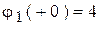 .
.
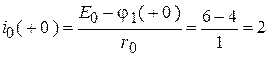 ;
; 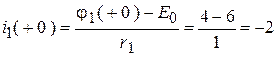 ;
;
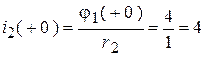 ;
; 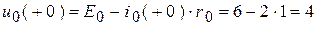 .
.
4. Рассчитаем НУР постоянного тока:
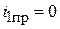 ;
; 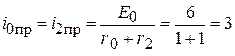 ;
;
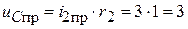 ;
; 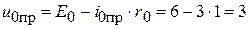 .
.
Начальные значения принужденных составляющих − те же самые величины  .
.
5. Составим характеристическое уравнение и найдем его корень (рис.1. 46):
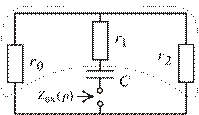 Рис. 1.46
Рис. 1.46
|
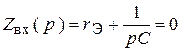 ;
; 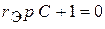 ;
;
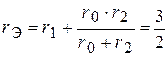 .
.
Решая уравнение, нашли: 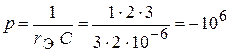 ,
,
Постоянная времени и длительность переходного процесса равна:
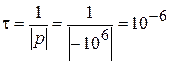 (с);
(с); 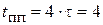 (мс).
(мс).
6. Определим постоянные интегрирования:
В общем виде: 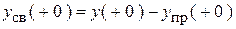 .
.
7. Переменные функции:
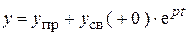 .
.
Решение сведем в таблицу. Так же построим графики рассматриваемых функций (рис. 1.47).
В момент коммутации, как видно на графике 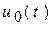 (см. рис. 1.46), напряжение
(см. рис. 1.46), напряжение 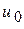 на полюсах ав источника моментально падает до величины его ЭДС
на полюсах ав источника моментально падает до величины его ЭДС 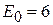 (В) и
(В) и  (В), а режим работы источника по его вольтамперной характеристике мгновенно из точки, помеченной как
(В), а режим работы источника по его вольтамперной характеристике мгновенно из точки, помеченной как 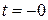 , мгновенно перемещается в точку, помеченную как
, мгновенно перемещается в точку, помеченную как 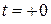 . Затем, за время всего переходного процесса режим работы сползает к точке, помеченной как
. Затем, за время всего переходного процесса режим работы сползает к точке, помеченной как 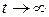 до принужденных значений
до принужденных значений 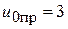 (В) и
(В) и 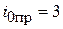 (А).
(А).
Конденсатор во время переходного процесса разряжается отрицательным током 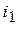 от начального
от начального 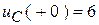 (В) до установившегося напряжения
(В) до установившегося напряжения 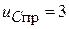 (В).
(В).
На графиках представлена полная картина переходного процесса. Здесь прослеживаются все уравнения цепи:
Нагрузка  подключается непосредственно к полюсам источника. Поэтому напряжения
подключается непосредственно к полюсам источника. Поэтому напряжения 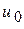 и
и 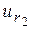 во время переходного процесса совмещены.
во время переходного процесса совмещены.
 Рис. 1.47
Рис. 1.47
|
Задача 4. Переходный процесс в цепи первого порядка с двумя емкостями и с постоянным источником питания (рис. 1.48).
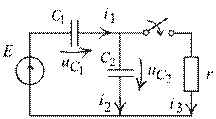 Рис. 1.48
Рис. 1.48
|
Условие:
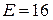 ( В );
( В ); 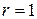 ( Ом );
( Ом ); 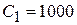 ( мкФ ),
( мкФ ), 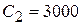 ( мкФ ).
( мкФ ).
Определить функции изменения токов
и напряжения на конденсаторах.
Решение:
1. В старом установившемся режиме (рис. 1.49) цепь представляет собой
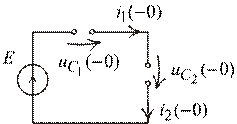 Рис. 1.49
Рис. 1.49
|
электростатическую систему. Нужно разделить напряжение источника между двумя последовательно соединенными емкостями. Объединенные прокладки последовательных конденсаторов имеют один общий заряд 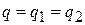 , то есть
, то есть  . Значит:
. Значит: 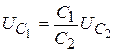 .
.
Из второго уравнения Кирхгофа:
 ,
,
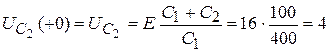 ,
,
Следовательно:
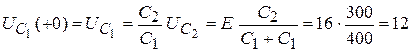 .
.
2. Зафиксируем ННУ: 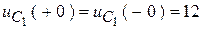 .
.
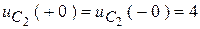 .
.
3. Определим ЗНУ. По схеме замещения для момента времени 
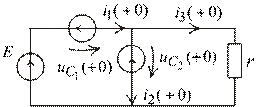 Рис. 1.50
Рис. 1.50
|
(рис. 1.50) из-за идеализации источника питания не позволяет определить начальные значения токов 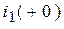 и
и 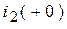 . Но можно рассчитать ток в третьей ветви:
. Но можно рассчитать ток в третьей ветви:
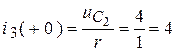 .
.
Значит, постоянные интегрирования будем находить только для трех функций: 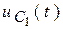 ,
, 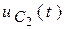 и
и 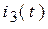 .
.
4. Рассчитаем НУР постоянного тока (рис. 1.51):
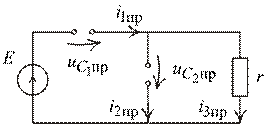 Рис. 1.51
Рис. 1.51
|
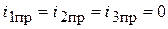 ;
;
 ;
;
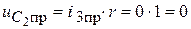
5. Составим характеристическое уравнение и найдем его корень (рис.1. 52):
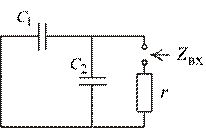 Рис. 1.52
Рис. 1.52
|
 ;
;
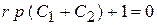 .
.
Решая уравнение, нашли:
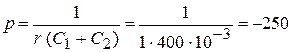 .
.
Постоянная времени и длительность переходного процесса равна:
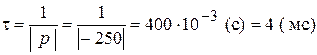 ,
, 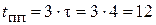 (мс).
(мс).
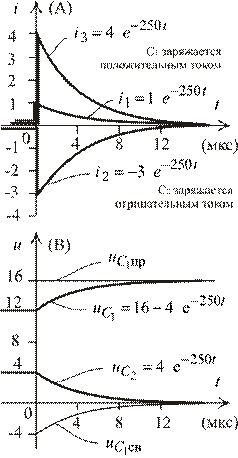 Рис. 1.53
Рис. 1.53
|
6. Определим постоянные интегрирования:
В общем виде:
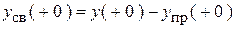 .
.
Для конкретных функций:
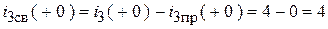 ;
;
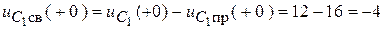
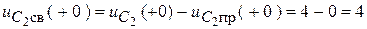
7. Переходные функции:
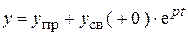 .
.
Решение сведем в таблицу:
| СУР | НУ | НУР | ПИ | ПФ | |
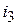
| −1 | 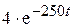
| |||
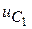
| −3 | 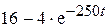
| |||
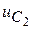
| 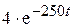
|
Токи в емкостях найдем из дифференциальных зависимостей;
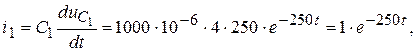
 .
.
Для токов и напряжения 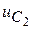 наблюдается только свободный процесс.
наблюдается только свободный процесс.
8. Графики переходных функций (рис.1.53).
9. Другой вариант коммутации в этой же схеме (рис. 1.54):
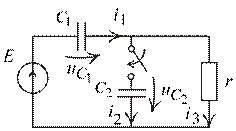 Рис.1.54
Рис.1.54
|
Просмотрим бегло все позиции расчета переходного процесса.
1) СУР и ННУ:
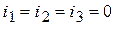 ;
; 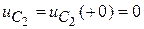 ;
;
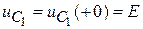 .
.
2) НУР – такой же, как и старый.
Значит:
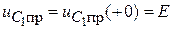 ,
, 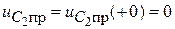 .
.
3) Характеристическое уравнение то же
самое, что и в первом варианте.
4) Переходные функции:
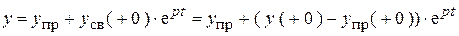 ,
,
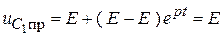 ,
,
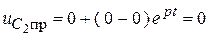 .
.
В цепи не будет переходного процесса. Это предсказуемый результат. Незаряженный конденсатор  подключается на нулевое напряжение. Очевидно, что ничего не произойдет.
подключается на нулевое напряжение. Очевидно, что ничего не произойдет.
10. Еще один вариант коммутации в заданной схеме (рис.1.55):
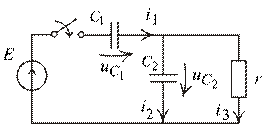 Рис.1.55
Рис.1.55
|
Емкостный контур, как и в первом варианте задачи, понизит порядок дифференциального уравнения до первого. Но в силу физических законов коммутации источник не в состоянии мгновенно поделить своё напряжение между емкостями левого контура, что делает предположение о мгновенной коммутации некорректным. Это небольшой аванс читателю. Расчет переходных процессов в цепях с некорректной коммутацией рассмотрим в следующей главе.
Задача 5. Цепь с синусоидальным источником ЭДС (рис.1.56).
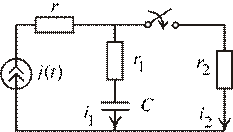 Рис. 1.56
Рис. 1.56
|
Условия:
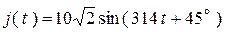 (А);
(А);
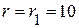 (Ом);
(Ом); 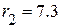 (Ом);
(Ом);
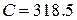 (мкФ).
(мкФ).
Определить закон изменения тока 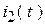
Решение:
1. Рассмотрим СУР.
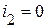 ,
,
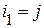 ,
,
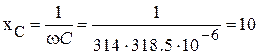 ,
,
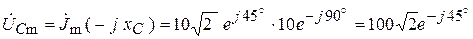 ,
,
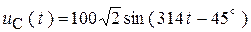 ,
,
В конце СУР: 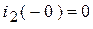 ;
; 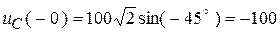 .
.
2. Зафиксируем ННУ:  .
.
3. Определим ЗНУ для искомого тока по схеме замещения (рис. 1.55) для 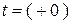 .
.
Начальные значения источника тока:
 .
.
В схеме один независимый контур. Для расчета выбираем метод контурных токов (одно уравнение для контура ( I )). Ток во второй ветви формируется только одним контурным током: 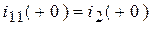 . Второй контурный ток задается только источником тока:
. Второй контурный ток задается только источником тока: 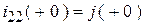 . Контурная ЭДС формируется только одним источником:
. Контурная ЭДС формируется только одним источником: 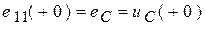 :
:
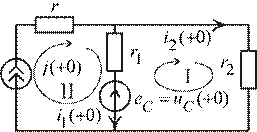 Рис. 1.57
Рис. 1.57
|
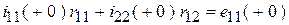 .
.
Откуда имеем:
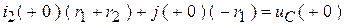 .
.
С учетом этого уравнения запишем так:
 ,
,
или:
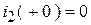 .
.
4. Рассчитаем НУР синусоидального тока и принужденную составляющую искомой функции:
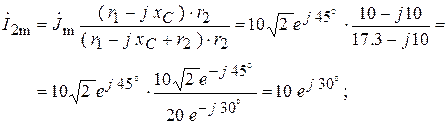
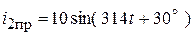 ;
;
Начальные значение принужденной составляющей:
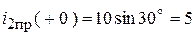 .
.
Период: 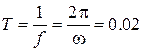 .
.
5. Составим характеристическое уравнение и найдем его корень (рис. 1. 58):
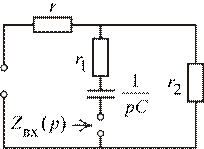 Рис. 1.58
Рис. 1.58
|
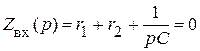 ,
,
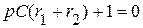 ,
,
Решая уравнение, нашли: 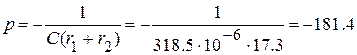 .
.
Постоянная времени и длительность переходного процесса равна:
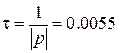 (с),
(с), 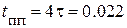 (с).
(с).
Переходный процесс практически заканчивается за время одного периода.
6. Определим постоянные интегрирования:
В общем виде: 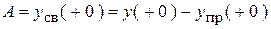 .
.
Следовательно, для тока 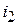 :
: 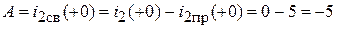 .
.
7. Переменная функция:
В общем виде: 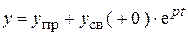 .
.
Тогда, для тока 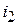 :
:
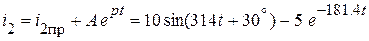 .
.
8. Построим график для найденной функции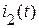 (рис. 1.59):
(рис. 1.59):
 Рис. 1.59
Рис. 1.59
|
Задача 6.Реакция цепи первого порядка на импульсное возмущение экспоненциальной формы (рис.1.60.)
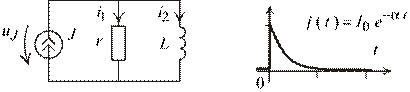 Рис. 1.60
Рис. 1.60
|
Определить законы изменения всех токов и напряжения на источнике питания.
Решение:
1. Рассмотрим СУР.
Источник отключен: 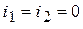 ;
; 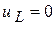 .
.
В конце СУР: 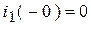 ;
; 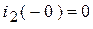 ;
; 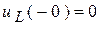 .
.
2. Зафиксируем ННУ: 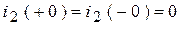 .
.
3. Определим ЗНУ: по первому закону коммутации индуктивность разрывает ветвь в расчетной схеме для 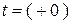 :
:
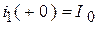 .
.
4. Новый установившийся режим − нулевой. Не может служить частным решением неоднородного дифференциального уравнения.
5. Уравнения цепи:
Из системы: 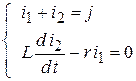
 для тока для тока 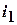 получим: получим:
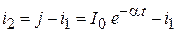 ; ;
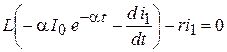 ; ;
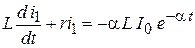 ; ;
| для тока 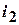 получим: получим:
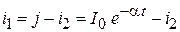 ; ;
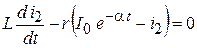
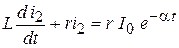 ; ;
|
Обозначив 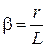 , запишем уравнения в конечной форме: , запишем уравнения в конечной форме:
| |
 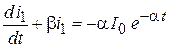
| 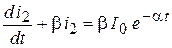
|
Коэффициенты левой части уравнения одинаковы. Различают только свободные члены (правые части).
6. Частное решение неоднородного дифференциального уравнения. Ищем в виде правой части. ( Метод неопределенных коэффициентов).
Для тока 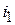 : :
 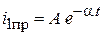 ; ;
| Для тока 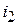 : :
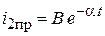 ; ;
|
| Подставим эти решения в уравнения для токов: | |
  ; ;
| 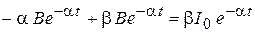 ; ;
|
| После сокращения на общий множитель, получим: | |
 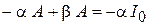 ; ;
| 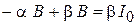 ; ;
|
 Отсюда и находятся неопределенные ранее коэффициенты: Отсюда и находятся неопределенные ранее коэффициенты:
| |
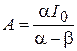 ; ;
| 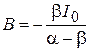 ; ;
|
| тогда: | |
 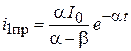
| 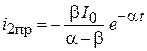
|
7. Постоянные интегрирования: 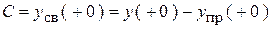
 Для тока Для тока 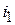 : :
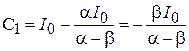
| Для тока 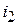 : :
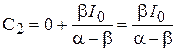
|
8. Характеристическое уравнение и его корень:
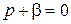 ;
;
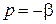 .
.
9. Переходные функции: 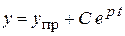 .
.
 Для тока Для тока 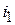 : :
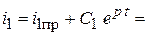
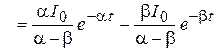 . .
| Для тока 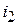 : :
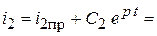
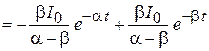 . .
|
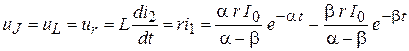 . .
|
6. Проверка: 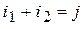
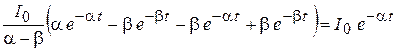 ;
;
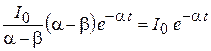 .
.
7. Переходные функции и графики при:
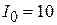 (А);
(А); 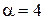 ( 1/с);
( 1/с); 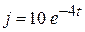 (А);
(А); 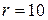 (Ом);
(Ом); 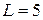 (Гн.).
(Гн.).
Тогда:
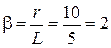 (1/с);
(1/с);
 (1/с).
(1/с).
Постоянные времени и время переходного процесса:
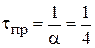 (с);
(с);
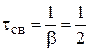 (с).
(с).
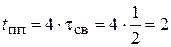 (с).
(с).
В схеме один накопитель. Это цепь первого порядка, но переходные функции как в цепи второго порядка. Это источник сформировал принужденную составляющую в форме свободной экспоненты.
Графики представлены на рис. 1.61
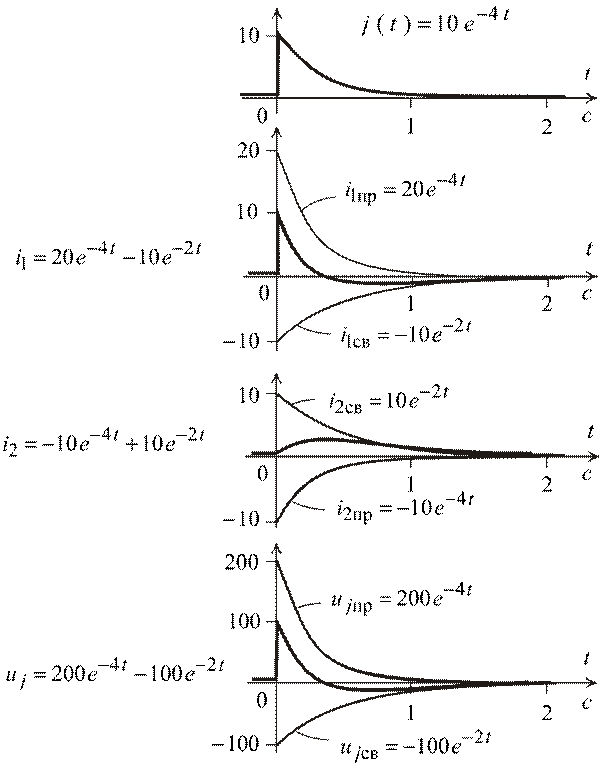 Рис. 1.61
Рис. 1.61
|
Дата добавления: 2018-09-24; просмотров: 2622;
