В переходном процессе
1.В цепи с одним реактивным накопителем 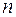 =1. В цепи с двумя различными ( L и C ) накопителями
=1. В цепи с двумя различными ( L и C ) накопителями 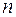 =2.
=2.
2.В других случаях n может быть меньше суммарного числа реактивных элементов.
 Рис. 1.19
Рис. 1.19
|
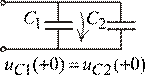 Рис. 1.20
Рис. 1.20
|
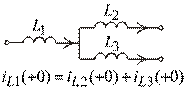 Рис. 1.21
Рис. 1.21
|
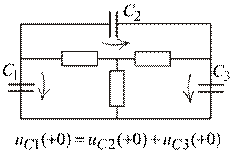 Рис. 1.22
Рис. 1.22
|
Порядок уравнения совпадает с числом слагаемых общего решения однородного уравнения 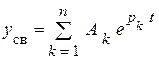 . Каждое слагаемое суммы можно формально рассматривать по принципу наложения как реакцию от отдельно взятого источника. Для свободного процесса это внутренние источники (реактивные накопители), запас энергии, которых в момент коммутации определяется значениями
. Каждое слагаемое суммы можно формально рассматривать по принципу наложения как реакцию от отдельно взятого источника. Для свободного процесса это внутренние источники (реактивные накопители), запас энергии, которых в момент коммутации определяется значениями 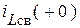 и
и 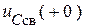 . Но слагаемые в решении
. Но слагаемые в решении 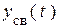 линейно независимы, значит внутренние источники, формирующие их, также должны быть линейно независимыми. Следовательно, порядок дифференциального уравнения равен числу реактивных накопителей, начальные условия для которых являются линейно независимыми. По этой причине:
линейно независимы, значит внутренние источники, формирующие их, также должны быть линейно независимыми. Следовательно, порядок дифференциального уравнения равен числу реактивных накопителей, начальные условия для которых являются линейно независимыми. По этой причине:
1). Последовательные индуктивности при определении порядка 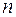 следует считать одним элементом, т.к. (рис. 1.19):
следует считать одним элементом, т.к. (рис. 1.19):
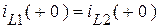 .
.
2). Параллельные емкости при определении порядка n следует считать одним элементом, т.к. (рис. 1.20):
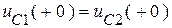 .
.
3). Если в схеме после исключения идеальных источников имеется узел или сечение с индуктивными ветвями, одно из независимых начальных условий является суммой других (рис. 1.21):
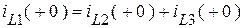 .
.
Такой объект уменьшает 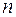 на 1.
на 1.
4). Если в пассивной схеме есть чисто емкостный контур, одно из начальных условий равно сумме напряжений на других емкостях (рис. 1.22):
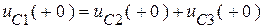 .
.
Такой контур тоже уменьшает 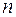 на 1.
на 1.
Вывод:
Наивысший порядок уравнения определяется по формуле:
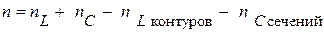
Здесь:
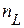 – число индуктивностей после упрощения 1;
– число индуктивностей после упрощения 1;
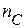 – число емкостей после упрощения 2;
– число емкостей после упрощения 2;
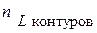 – число индуктивных узлов (сечений) 3;
– число индуктивных узлов (сечений) 3;
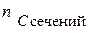 – число чисто емкостных контуров 4.
– число чисто емкостных контуров 4.
В каких-то схемах при определенном соотношении параметров, этот порядок может еще уменьшиться.
3.Пример
В послекоммутационных схемах:

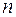 =1 =1
| 
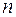 =1 =1
| 
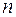 =2 =2
| |
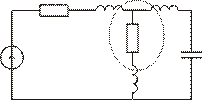
 =3 =3
| 
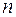 =3 =3
| ||

|
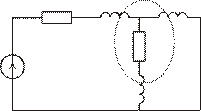
Пример для самостоятельного обдумывания:
Здесь нет последовательных индуктивностей или параллельных емкостей. Но на рисунке указаны пять существующих здесь индуктивных сечений.
Значит: 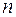 =6−5=1.
=6−5=1.
Дата добавления: 2018-09-24; просмотров: 508;
