Зависимые начальные условия
Значения всех других функций и значения производных от всех без исключения функций в момент времени 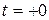 называют зависимыми начальными условиями. Это, например,
называют зависимыми начальными условиями. Это, например, 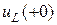 ,
, 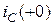 ,
, 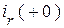 ,
, 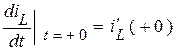 и т.д. Поведение этих функций в момент
и т.д. Поведение этих функций в момент 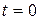 визуально неопределимо. Может оказаться, например, что
визуально неопределимо. Может оказаться, например, что 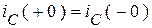 , или
, или 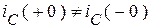 . Все зависит от содержания схемы. Поэтому эти начальные условия называются зависимыми, они не могут быть извлечены из старого установившегося режима и требуют специального расчета в каждой конкретной ситуации.
. Все зависит от содержания схемы. Поэтому эти начальные условия называются зависимыми, они не могут быть извлечены из старого установившегося режима и требуют специального расчета в каждой конкретной ситуации.
Расчет зависимых начальных условий:
1. Сначала рассчитываются независимые начальные условия.
2. Составляется система независимых уравнений Кирхгофа послекоммутационной схемы для мгновенных значений 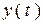 .
.
3. В уравнения на место независимой переменной 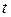 подставляется её конкретное значение
подставляется её конкретное значение 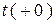 . Все функции превращаются в числа. Система из дифференциальной превращается в алгебраическую, где искомыми величинами являются начальные значения
. Все функции превращаются в числа. Система из дифференциальной превращается в алгебраическую, где искомыми величинами являются начальные значения 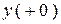 . Здесь внешние источники представлены значениями
. Здесь внешние источники представлены значениями 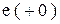 и
и 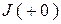 , а функции
, а функции 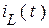 и
и 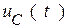 известными начальными значениями
известными начальными значениями 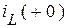 и
и 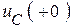 .
. 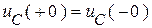 .
.
4. Поскольку это полная система независимых уравнений, количество зависимых начальных условий 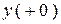 равно количеству уравнений, и система всегда имеет однозначные решения. Зависимые начальные условия являются решениями этой системы.
равно количеству уравнений, и система всегда имеет однозначные решения. Зависимые начальные условия являются решениями этой системы.
5. В цепи второго порядка для каждой функции 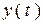 нужно будет определять две постоянных интегрирования, для чего потребуются начальные условия первых производных
нужно будет определять две постоянных интегрирования, для чего потребуются начальные условия первых производных 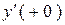 .
.
Сначала, исходя из дифференциальной связи токов и напряжений на реактивных накопителях, рассчитываются начальные значения 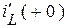 и
и 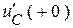 . Из соотношения
. Из соотношения 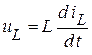 следует, что
следует, что 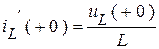 . Аналогично из связи
. Аналогично из связи 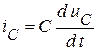 определяем, что
определяем, что 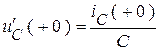 .
.
Далее надо продифференцировать систему уравнений послекоммутационной схемы и записать её для мгновенных значений при 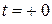 . Здесь будут известны уже начальные значения возмущений
. Здесь будут известны уже начальные значения возмущений 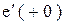 ,
, 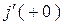 и рассчитанные ранее
и рассчитанные ранее 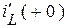 ,
, 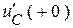 . В такой системе число уравнений равно количеству неизвестных еще начальных значений производных.
. В такой системе число уравнений равно количеству неизвестных еще начальных значений производных.
4. Пример:Рассчитаем все начальные условия для схемы (рис. 1.9):
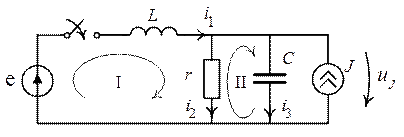 Рис. 1.9
Рис. 1.9
|
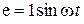 (В),
(В),
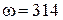 (1/с),
(1/с),
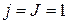 (А),
(А),
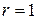 (Ом),
(Ом),
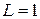 (мГн),
(мГн),
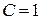 (мкФ).
(мкФ).
Решение:
1. Старый установившийся режим (СУР).
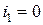 ;
; 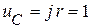 .
.
В конце старого установившегося режима:
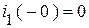 ,
, 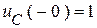 .
.
2. Независимые начальные условия (ННУ):
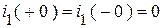 ,
, 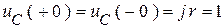 .
.
3. Начальные значения возмущений:
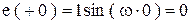 ;
; 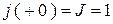 .
.
4. Зависимые начальные условия:
Начальные значения функций:
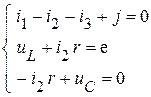 для
для 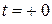
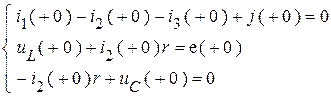
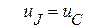
Здесь известны: 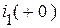 ,
, 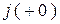 ,
, 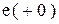 ,
, 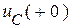 .
.
Решая систему, получили:
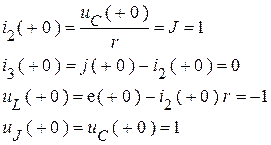
Определим начальные значения производных из дифференциальных соотношений:
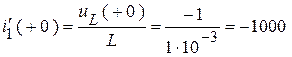 А/с;
А/с;
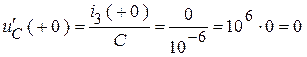 В/с.
В/с.
Уже из этих результатов, определяющих очень большие начальные скорости некоторых переходных функций, следует заключение о скоротечности электромагнитных переходных процессов.
Продифференцируем систему уравнений Кирхгофа:
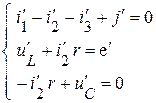 для
для 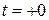
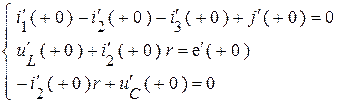
Т.к. 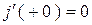 и
и 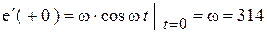 , то, решая систему, получим:
, то, решая систему, получим:
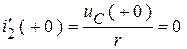
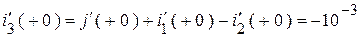
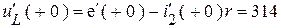
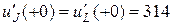 .
.
5. Схема замещения цепи для расчета зависимых начальных значений функций 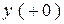
В момент 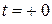 из конца старого установившегося режима сохраняются значения
из конца старого установившегося режима сохраняются значения 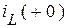
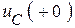 . Эти известные величины можно задать источниками тока
. Эти известные величины можно задать источниками тока 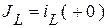 и ЭДС
и ЭДС 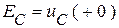 . В соответствии с принципом компенсации
. В соответствии с принципом компенсации 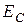 направляется навстречу току в ветви (т.е. навстречу напряжению
направляется навстречу току в ветви (т.е. навстречу напряжению 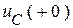 ). Если при этом внешние источники представить величинами
). Если при этом внешние источники представить величинами 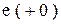 и
и 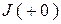 , то во всех ветвях схемы будут наблюдаться мгновенные значения остальных функций
, то во всех ветвях схемы будут наблюдаться мгновенные значения остальных функций 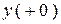 и получится схема замещения цепи для расчета начальных значений функций. При нулевых независимых начальных условиях индуктивность разрывает ветвь, а емкость является короткозамкнутым участком. (Рис. 1.10)
и получится схема замещения цепи для расчета начальных значений функций. При нулевых независимых начальных условиях индуктивность разрывает ветвь, а емкость является короткозамкнутым участком. (Рис. 1.10)
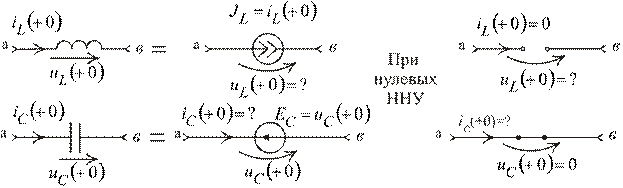 Рис. 1.10
Рис. 1.10
|
Для выше рассмотренного примера имеем:
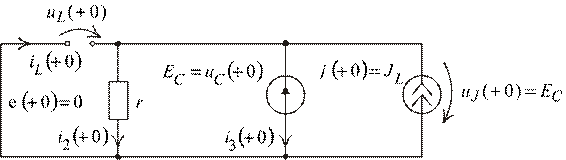 Рис. 1.11
Рис. 1.11
|
Схема (рис. 1.11) описывается теми же самыми алгебраическими уравнениями. Принципы построения схемы замещения элементарны.
Смысл построения такой схемы заключается в расширении возможностей расчета зависимых начальных условий 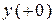 . Для ее расчета можно воспользоваться любым известным методом (методом контурных токов, методом узловых потенциалов и т.д.).
. Для ее расчета можно воспользоваться любым известным методом (методом контурных токов, методом узловых потенциалов и т.д.).
6.Схема замещения не содержит реактивных элементов. Значит, зависимые начальные условия для 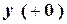 не зависят от реактивных параметров
не зависят от реактивных параметров 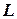 и
и 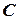 .
.
От реактивных параметров зависят начальные значения производных 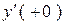 .
.
Дата добавления: 2018-09-24; просмотров: 2128;
