Математическая характеристика уравнения и способ отыскания его решения

Это:

1. Обыкновенное дифференциальное уравнение (одна независимая переменная – время ).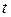

2. Линейное дифференциальное уравнение ( 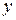и её производные входят в первой степени).

3. Дифференциальное уравнение с постоянными коэффициентами (комбинации постоянных параметров, зависящие от структуры схемы).

4. Неоднородное уравнение (с правой частью), 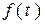– функция времени, которая является линейной комбинацией возмущений внешних источников.

5. Порядок уравнения зависит от числа реактивных накопителей, структуры схемы и соотношения параметров. Но он не более общего числа реактивных элементов. В нашем примере он равен двум (два накопителя – катушка и конденсатор).

Итак: для линейной цепи это обыкновенное линейное неоднородное дифференциальное уравнение с постоянными коэффициентами.

Математический вид уравнения определяет способ отыскания его решения. Для уравнения такого вида решение отыскивается в виде суммы двух линейно независимых слагаемых. В электротехнической терминологии это принужденная и свободная функции.

.

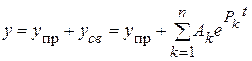Здесь:

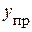– частное решение неоднородного уравнения. Математически оно отыскивается в виде правой части. Значит, вид этого решения полностью определяется источниками. Поэтому в электротехнике это решение и называют принужденной составляющей. Рассчитывается эта функция известными математическими методами (например: методом неопределенных коэффициентов).

В двух существенно важных случаях, смысловое содержание 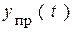позволяет обойти формальные математические способы отыскания этого решения.

В цепи с постоянными источниками правая часть уравнения – постоянное число. Решение 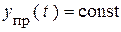должно удовлетворять уравнениям цепи. Постоянные решения наблюдаются в НУР. Поэтому 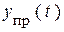естественным образом отождествляется с решениями в НУР. Для определения 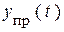любой функции нужно просто рассчитать НУР цепи постоянного тока.

Аналогично в цепи с синусоидальными источниками 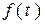– синусоидальная функция. Решения 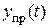для всех функций синусоиды, удовлетворяющие уравнениям схемы. Они естественно находятся из расчета нового синусоидального режима работы схемы.

Свободная составляющая 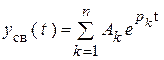– общее решение однородного дифференциального уравнения. Это множество решений уравнения без правой части. Оно не формируется внешними источниками. Приравнивая к нулю правую часть уравнения, мы тем самым исключаем из схемы внешние источники энергии. Однородным уравнением описывается цепь с исключенными источниками. Поэтому решение 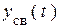в электротехнике и называют свободной составляющей.

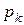Число слагаемых суммы равно порядку дифференциального уравнения. Здесь – постоянные интегрирования, а - корни характеристического уравнения.

Во время переходного процесса в цепи с источниками существует функция 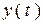, и нельзя физически выделить её слагаемые 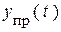и 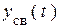. Такое разделение следует рассматривать только как удачно найденный математический прием отыскания решения.

Физически в чистом виде принужденный процесс можно наблюдать только в новом установившемся режиме в цепи с постоянными или синусоидальными источниками. Свободный процесс в чистом виде можно наблюдать как переходную функцию в цепи без источников.