Постоянная интегрирования для любой функции в цепи первого порядка равна начальному значению ее свободной составляющей.

Можно записать:

.

3.Содержание расчета переходного процесса в цепи первого порядка.

Для составления решения рассматривается ряд задач, в результате чего определяются все компоненты искомой функции.

Рис.1.26

4.Для иллюстрации характера переходного процесса в цепи первого порядка рассмотрим два элементарных примера с одноконтурными схемами при постоянном и синусоидальном источниках.

Пример 1: Включение 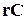цепи на постоянное напряжение .

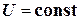Конденсатор предварительно зарядим до напряжения .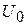

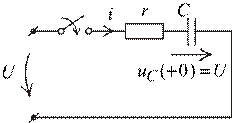Рис. 1.27

СУР: ; ; .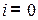

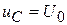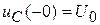НУ: ; .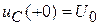

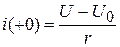НУР: ; ; .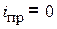

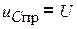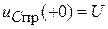ПИ: .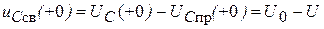

Характеристическое уравнение и его корень:

; .

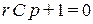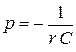Полное решение для напряжения :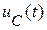

.

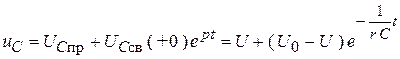Ток 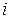из дифференциальной связи :

.

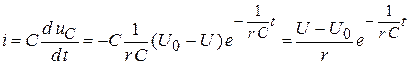Анализ решения: Деформация процесса в зависимости от начальных условий (рис. 1.28).

Рис. 1.28

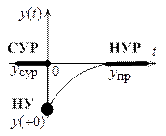Рис. 1.29

В цепи с постоянными источниками , а для 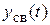- экспонента. Значит, переходная функция 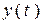представляет собой кривую, которая от значения 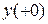монотонно и асимптотически приближается к новому установившемуся режиму 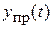. Это обстоятельство позволяет качественно представить переходный процесс, для чего необходимо рассчитать только старый установившийся режим, начальные условия и новый установившийся режим (рис. 1.29).

Пример 2: Включение нагрузки на синусоидальное напряжение.

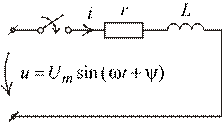Рис. 1.30

СУР: ; ; .

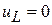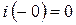НУ: ; .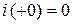

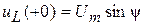НУР: ;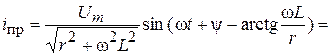

.

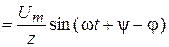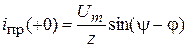ПИ: .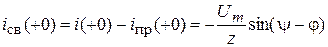

Характеристическое уравнение и его корень: ; .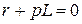

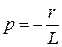Полное решение:

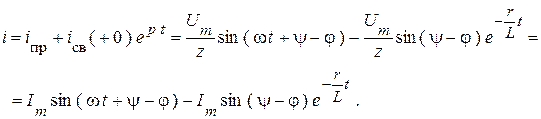
Напряжение на индуктивности 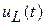найдем из дифференциальной связи:

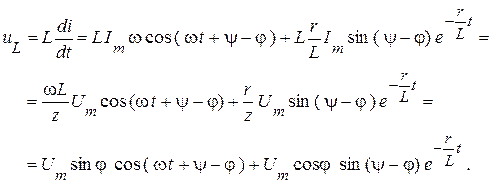
Анализ решения: Деформация процесса в зависимости от момента включения источника и соотношения параметров.

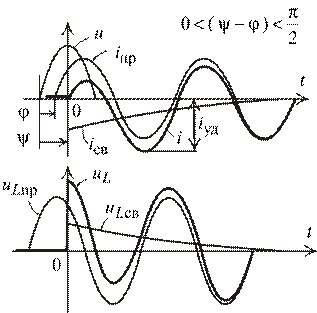Рис. 1.31

На синусоидальный ток нового установившегося режима накладывается свободная экспонента (рис. 1.31), начальное значение которой 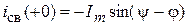определяется двумя независящими друг от друга факторами. С одной стороны это начальная фаза 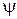, зависящая от момента включения. Это случайный фактор. С другой стороны это угол сдвига фаз 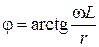нового установившегося режима, зависящим от соотношения параметров схемы. Теми же параметрами определяется и постоянная времени 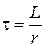, от которой зависит скорость установления принужденного режима. В какие-то моменты максимальное значение тока может превышать амплитуду 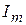. Его называют ударным значением .

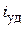Два крайних случая (рис. 1.32).

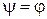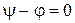В одном крайнем случае, когда и , постоянная интегрирования превращается в нуль, переходный процесс будет отсутствовать и сразу после включения наступит новый установившийся режим: .

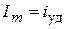На левом рисунке сохранены параметры, угол сдвига остался тем же, что и в первом варианте, где рассматривался общий случай. Изменен только момент включения.

На правом рисунке представлен вариант, приближенный к другому крайнему случаю. Соотношение параметров таково, что

угол 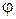приближен к 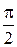, что затягивает затухание свободной функции вследствие увеличения постоянной времени 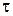. Момент включения подобран так, чтобы 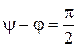и 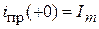. Тогда максимально возможное начальное значение свободной функции за полпериода практически не затухает и ударное значение тока 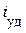приближается к двойному амплитудному значению. Таким образом: .

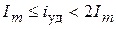Среднестатистическое отношение 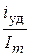наблюдается в пределах от 1,3 в низковольтовых до 1,8 в высоковольтовых цепях.

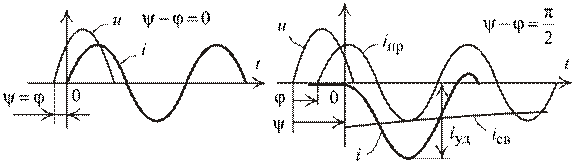Рис. 1.32

5.Далее изложенный материал иллюстрируется решением нескольких задач по расчету переходного процесса в цепи первого порядка.