Сложный сигнал и ряд Фурье
На рис.3 показан двумерный вектор F в комплексной плоскости. Этот вектор имеет действительную составляющую а в направлении действительной оси и мнимую составляющую ib в направлении мнимой оси. Вектор F представлен суммой этих составляющих, то есть
| F = a + ib. | (13) |
Вектор F целесообразно представить при помощи его амплитуды (модуля)  и фазового угла q. Из рис.3 следует, что составляющие вектора F полярных и прямоугольных координатах связаны друг с другом соотношениям (13)
и фазового угла q. Из рис.3 следует, что составляющие вектора F полярных и прямоугольных координатах связаны друг с другом соотношениям (13)

Из последних выражений следует, что:
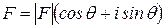
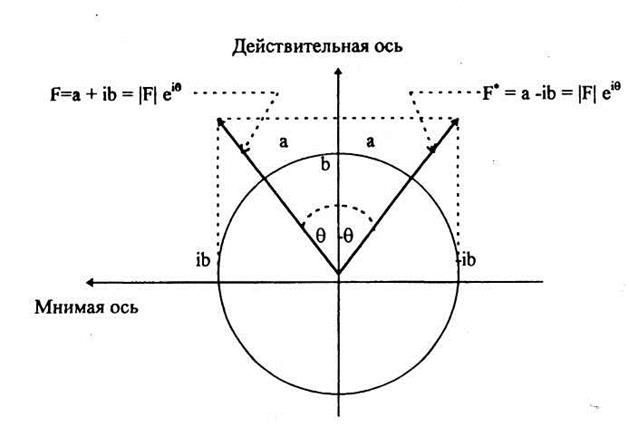
Рис.3. Двумерный вектор в комплексном представлении
Учитывая формулу Эйлера, вектор F можно представить комплексным вектором (экспоненциалом)
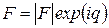 . .
|
Комплексно сопряженным вектором F* называется вектор, имеющий с вектором F одну точку приложения (в данном случае это точка 0), одинаковую абсолютную величину (в данном случае |F|) и одинаковый по абсолютной величине, но взятый с противоположным знаком полярный угол q.
Пусть вектор F равномерно вращается вокруг точки 0 и его абсолютная величина |F| при этом не изменяется. Тогда фазовый угол является линейно изменяющейся функцией времени
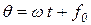 , ,
| (14) |
где обозначения соответсвуют (12). Используя зависимость для угловой частоты, получим
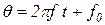 , ,
| (15) |
где f- частота, f=1/T, где Т- период.
Из сказанного следует, что ехр(if0) является единичным вектором с соответствующим фазовым углом f0.
Простая гармоника с амплитудой А, исходным фазовым углом q и частотой показана на рис.4,а. Соответствующее графическое представление невыгодно с точки зрения того, что горизонтальная ось (ось X) является осью как времени, так и фазового угла. Кроме того, полезное для математической обработки представление отрицательных частот или бессмысленно или, по меньшей мере, неясно.
На рис.4,6 показано представление гармонической составляющей в виде суммы двух векторов, вращающихся в противоположных друг другу направлениях и имеющих каждый амплитуду A/2. Один из этих векторов имеет исходный фазовый угол q и вращается с частотой f, в то время как другой имеет исходный угол - q и совершает вращательное движение с частотой - f. Отрицательная частота при векторном представлении имеет ясный физический смысл и указывает на происходящее с отрицательным знаком изменение фазового угла и, по существу, необходима для описания вращения векторов в противоположных друг другу направлениях.
Рис.4,6 показывает положение составляющих векторов в начале отсчета времени. При вращении этих векторов результат их векторного сложения всегда совпадает с действительной осью (мнимые составляющие аннулируют друг друга) и соответствуют показанной на рис.4,а синусоиде. Эквивалентность представлений на рис.4,а и 4,6 определена математическим равенством
 , ,
| (16) |
Итак:
анализ искомого решения уравнения движения механической сиcтемы сводится прежде всего к оценке параметров отдельной гармоники с частотой f;
из полученного результата возникает вопрос и возможности представления действительного числа в виде суммы вида
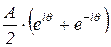 , ,
|

Рис.4. Гармоническая составляющая A cos(2pft + f) (a);
гармоническая составляющая, представленная векторной суммой вращающихся в противоположных друг другу направлениях двух векторов (б)
Математической основой частотного анализа периодической функции является ее разложение в ряд Фурье. Преобразование Фурье принимает различные формы в зависимости от вида анализируемых функций. Однако все виды преобразования Фурье имеют общим предположение того, что исследуемые сигналы состоят из определенного (возможно бесконечного) числа синусоидальных и/или косинусоидальных составляющих (гармоник) с различными частотами, причем отдельные составляющие имеют определенные амплитуды и фазовые углы.
Если функция f(t) периодическая с периодом Т = 2l, то функциональный ряд вида
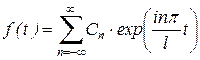 , ,
| (17) |
является комплексной формой ряда Фурье. Комплексные коэффициенты С определяются по формуле
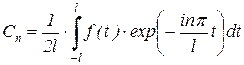 , (n=0,±1, ±2, ±3,…) , (n=0,±1, ±2, ±3,…)
| (17) |
Выражения 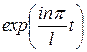 называются гармониками, а числа аn=np/l называются волновыми числами. Совокупность волновых чисел называется спектром.
называются гармониками, а числа аn=np/l называются волновыми числами. Совокупность волновых чисел называется спектром.
Возможны и другие формы записи выражения (17)
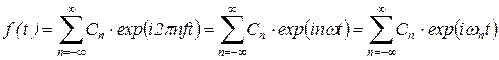 , ,
| (18) |
где wn = n f.
Таким образом, любой периодический сигнал может быть представлен в виде суммы простых гармоник.
Дата добавления: 2018-09-24; просмотров: 618;
