Z – ТРАНСФОРМАЦИЯ сигналов [4, 12, 22].

ЦИФРОВАЯ ОБРАБОТКА СИГНАЛОВ

Цифровая обработка сигналов оперирует с дискретными представлениями сигналов. Математика дискретных преобразований зародилась в недрах аналоговой математики еще в 18 веке в рамках теории рядов и их применения для аппроксимации функций, однако ускоренное развитие она получила в 20 веке после появления первых вычислительных машин. В принципе, в своих основных положениях математический аппарат дискретных преобразований подобен преобразованиям аналоговых сигналов и систем. Однако дискретность данных требует учета этого фактора, а его игнорирование может приводить к существенным ошибкам. Кроме того, ряд методов дискретной математики не имеет аналогов в аналитической математике.

Распространенным способом анализа дискретных цифровых последовательностей является z-преобразование (z-transform). Оно играет для дискретных сигналов и систем такую же роль, как для аналоговых – преобразование Лапласа. Большое значение z-преобразование имеет для расчетов рекурсивных цифровых систем обработки сигналов, а потому рассматривается отдельной темой перед началом изучения рекурсивных цифровых фильтров.

Z – ТРАНСФОРМАЦИЯ сигналов [4, 12, 22].

Определение z-преобразования. Z-преобразование представляет собой разложение функций в ряды степенных полиномов по z. Впервые z-преобразование введено в употребление П.Лапласом в 1779 и повторно "открыто" В.Гуревичем в 1947 году с изменением символики на z^-k. В настоящее время в технической литературе имеют место оба вида символики. На практическое использование преобразования это не влияет, т.к. смена знака только зеркально изменяет нумерацию членов полинома (относительно z⁰), числовое пространство которых в общем случае от -¥ до +¥. В дальнейшем в качестве основной будем использовать символику положительных степеней z, давая пояснения по особенностям отрицательной символики, если таковая имеется.

Произвольной непрерывной функции s(t), равномерно дискретизированной и отображенной отсчетами s_k = s(kDt), равно как и непосредственно дискретной функции, можно поставить в однозначное соответствие степенной полином по z, последовательными коэффициентами которого являются значения s_k:

s_k = s(kDt) Û TZ[s(kDt)] = 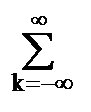s_k z^k = S(z). (8.1.1)

где z = s+jw - произвольная комплексная переменная. В показательной форме z = r×exp(-jj), где r = |z| = 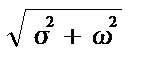, j = arg(z) =argtg(w/s).

Пример 1:s_k = {1, 2, 0, -1, -2, -1, 0, 0}.

S(z) = 1z⁰+2z¹+0z²-1z³-2z⁴-1z⁵+0z⁶+0z⁷ = 1+2z-z³-2z⁴-z⁵.

В каузальных системах значения импульсного отклика систем существуют при k ≥ 0 и уравнение (8.1.1) действует в одностороннем варианте:

H(z) = 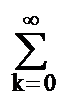h_k z^k.

В общем случае, z-преобразование – это степенной ряд с бесконечным количеством членов, поэтому он может сходиться не для всего пространства значений z. Область z, в которой z-преобразование сходится и значения S(z) конечны, называют областью сходимости.

Пример 2:Последовательность (сигнал) конечной длины, непричинная: s_-k = {1, 2, 3, 2, 1}, k = 0, 1, 2, 3, 4.

S(z) = 1z⁰+2z^-1+3z^-2+2z^-3+1z^-4 = 1+2/z+3/z²+2/z³+1/z⁴.

Очевидно, что S(z) = ∞ при z = 0. Область сходимости – все значения z, за исключением z = 0.

Пример 3:Последовательность конечной длины, причинная (как импульсный отклик каузальной системы): s_k = {1, 2, 3, 2, 1}, k = 0, 1, 2, 3, 4.

S(z) = 1+2z+3z²+2z³+z⁴.

S(z) = ∞ при z = ∞. Область сходимости – все значения z, за исключением z = ∞.

Пример 4:Последовательность конечной длины, двусторонняя (как импульсный отклик симметричного фильтра): s_k = {1, 2, 3, 2, 1}, k = -2, -1, 0, 1, 2.

S(z) = 1z^-2+2z^-1+3z⁰+2z¹+1z² = 1/z²+2/z+3+2z+z².

S(z) = ∞ при z = 0 и z = ∞. Область сходимости не включает точки z = 0 и z = ∞.

Пример 5:Последовательность бесконечной длины, причинная (как импульсный отклик рекурсивного интегрирующего фильтра): s_k = 0 при k < 0, s = 1 при k ≥ 0.

S(z) = z^-0+z¹+z²+z³+ … = 1+z+z²+z³+ … = 1/(1-z)

Ряд удовлетворяет условию сходимости только при |z| < 1.

Значения z, для которых S(z) = ∞, называются полюсами, а для которых S(z) = 0, называются нулями функции S(z). Как видно из примеров, для последовательностей конечной длины z-преобразование сходится везде кроме точки z=∞ для имеющих правостороннюю часть (k≥0), и точки z=0 для имеющих левостороннюю часть (k<0), в любых их комбинациях. Для бесконечных причинных последовательностей преобразование сходится везде внутри круга единичного радиуса с центром в начале координат.

По заданному или полученному в результате анализа какой-либо системы z-полиному однозначно восстанавливается соответствующая этому полиному функция путем идентификации коэффициентов степеней при z^k с k-отсчетами функции.

Пример 6:S(z) = 1+3z²+8z³-4z⁶-2z⁷ = 1z⁰+0z¹+3z²+8z³+0z⁴+0z⁵-0z⁶-2z⁷.

s_k = {1, 0, 3, 8, 0, 0, -4, -2}.

Смысл величины z в z-полиноме заключается в том, что она является оператором единичной задержки по координатам функции. Умножение z-образа сигнала s(k) на величину zⁿ означает задержку сигнала (сдвиг вправо по временной оси) на n интервалов: zⁿS(z) Û s(k-n). Чтобы убедиться в этом, достаточно в приведенном выше примере выполнить умножение многочлена S(z), например на z², выполнить обратное преобразование и получить новый сигнал s_k = {0, 0, 1, 0, 3, 8, 0, 0, -4, -2}.

Z-образы с положительными степенями z соответствуют каузальным (физически реализуемым) процессам и системам, которые работают в реальном масштабе времени с текущими и "прошлыми" значениями сигналов. При обработке информации на ЭВМ каузальность сигналов не относится к числу ограничений и возможно использование отрицательных степеней z, соответствующих отсчетам сигналов "вперед". Последнее применяется, например, при синтезе симметричных операторов фильтров, что позволяет производить обработку информации без внесения в сигнал фазовых искажений. При использовании символики z^-1 "прошлым" значениям соответствуют значения с отрицательными степенями z, "будущим" – с положительными.

Основное достоинство z-преобразований заключается в простоте математических операций со степенными полиномами, что имеет немаловажное значение при расчетах цифровых фильтров и в спектральном анализе.

Связь с преобразованиями Фурье и Лапласа. Запишем дискретный сигнал s_k в виде суммы весовых импульсов Кронекера:

s_k = s(kDt) = 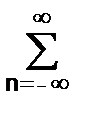s(nDt) d(kDt-nDt).

Определим спектр сигнала по теореме запаздывания:

S(w) = 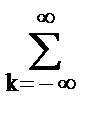s(kDt) exp(-jwkDt).

Выполним замену переменных, z = exp(-jwDt), и получим:

S(w) = 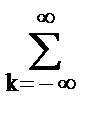s(kDt)×z^k = S(z).

Отсюда следует, что дискретное преобразование Фурье является частным случаем z-преобразования при z = exp(-jwDt).

Аналогичной подстановкой z = exp(-p) может осуществляться переход к дискретному преобразованию Лапласа. В общем виде:

S(w) = S(z), z = exp(-jwDt); S(p) = S(z), z = exp(-pDt). (8.1.2)

Обратное преобразование:

S(z) = S(w), w = ln z / jDt; S(z) = S(p), p = ln z/Dt. (8.1.3)

При отрицательной символике z связь между представлениями осуществляется соответственно подстановками z^-1 = exp(jwDt) и z^-1 = exp(p).

При z^k = exp(-jwkDt) z-преобразование представляет собой особую форму представления дискретных сигналов, при которой на полином S(z) можно ссылаться как на временную функцию (по значениям коэффициентов kDt), так и на функцию частотного спектра сигнала (по значениям аргумента w).

Отображение z-преобразования выполняют на комплексной z-плоскости с Re z и Im z по осям координат (рис. 8.1.1). В частности, спектральной оси частот w на z-плоскости соответствует окружность радиуса:

|z| = |exp(-jwDt)| = 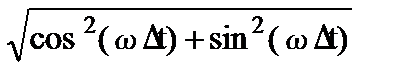= 1.

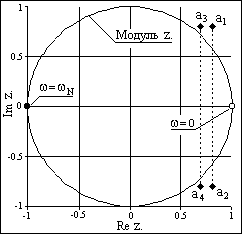Рис. 8.1.1. Комплексная z-плоскость

Подстановка значения какой-либо частоты w в z = exp(-jwDt) отображается точкой на окружности. Частоте w = 0 соответствует точка Re z = 1 и Im z = 0 на правой стороне оси абсцисс. При повышении частоты точка смещается по окружности против часовой стрелки, и занимает крайнее левое положение на частоте Найквиста w_N = p/Dt (Re z = -1, Im z = 0). Отрицательные частоты спектра отображаются аналогично по часовой стрелке на нижней полуокружности. Точки 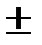w_N совпадают, а при дальнейшем повышении или понижении частоты значения начинают повторяться в полном соответствии с периодичностью спектра дискретной функции. Проход по полной окружности соответствует одному периоду спектра, а любая гармоника спектра сигнала задается на плоскости двумя точками, симметричными относительно оси абсцисс.

Сигналы и системы непрерывного времени очень часто описываются с помощью преобразования Лапласа. Если z=exp(-sDt), где s=s + jw, то

z = exp(-(s + jw)Dt) = exp(-sDt) exp(-jwDt).

Следовательно, |z| = exp(-sDt), arg(z) = wDt = 2pfDt = 2pf/f_D, где f_D - частота дискретизации, при этом ось w отображается на z-плоскости единичной окружностью, правая сторона s-плоскости отображается внутрь окружности, а левая сторона – на внешнюю сторону окружности. При использовании символики z^-1 отображение сторон s-плоскости на z-плоскости меняется местами.