ПРОСТРАНСТВО Z-ПОЛИНОМОВ [2, 12, 36].
Область сходимости. Полином S(z) (8.1.1) называют z-образом или z-изображением функции s(kDt). Преобразование имеет смысл для области тех значений z, в которой ряд S(z) сходится, т.е. сумма ряда представляет собой аналитическую функцию переменной z, не имеющую полюсов и особых точек:
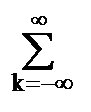 |sk||z|k < ∞
|sk||z|k < ∞
В общем случае, множества z, для которых полиномы S(z) сходится, образуют на z-плоскости определенные области, показанные на рис. 8.2.1.
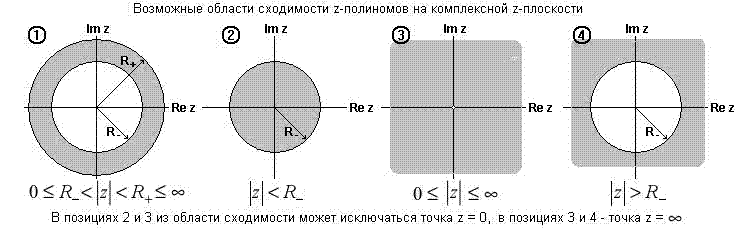
Рис. 8.2.1.
Из приведенной выше связи z-преобразования с преобразованием Фурье следует, что если функция s(t) имеет спектральное представление S(w), то единичная окружность |z| = |exp (-jw)| = 1 обязательно должна входить в область сходимости полинома S(z). И наоборот, если область сходимости полинома S(z) включает в себя единичную окружность, то дискретное преобразование Фурье функции s(t) – прообраза полинома S(z), должно существовать, а в противном случае – нет. Последнее следует из того, что z-преобразование, являясь более общим случаем преобразования дискретных функций, может существовать и для функций, для которых не существует преобразования Фурье. Примером этого может служить функция единичного скачка:
un = 1, n ≥ 0; un = 0, n < 0.
Для преобразования Фурье функции u(n) не выполняется условие абсолютной суммируемости (энергия функции бесконечна). Но для z-преобразования имеем:
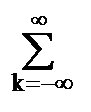 |uk||z|k =
|uk||z|k = 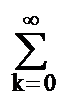 |z|k < ∞, при |z| < 1.
|z|k < ∞, при |z| < 1.
Примеры z-преобразования часто встречающихся на практике дискретных сигналов.
Импульсы Кронекера. В общем случае, для импульса Кронекера в произвольной точке числовой оси:
d(k-n) =1 при k=n, d(k-n) = 0 при k ≠ n.
Xd(z) = 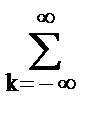 d(k-n) zk = zn.
d(k-n) zk = zn.
Для импульса Кронекера в нулевой точке соответственно Xd(z) = z0 =1. Ряд Xd(z) сходится на всей z-плоскости.
Функция Хевисайда (единичный скачок, причинная последовательность бесконечной длины, например, импульсный отклик рекурсивного интегрирующего фильтра).
x(k) = 0 при k < 0, x(k) = 1 при k ³ 0.
X(z) =  zk = zk.
zk = zk.
Ряд сходится при |z| < 1, при этом его сумма равна:
X(z) = 1/(1-z).
Z-преобразование действительно везде внутри круга единичного радиуса с центром в начале координат.
При использовании символики z-1:
X(z) = 1/(1-z-1) = z/(z-1), |z| > 1.
На границе области аналитичности функция X(z) имеет один простой полюс при z=1.
Экспоненциальная функция:
x(k) = 0 при k < 0, x(k) = ak при k ³ 0.
X(z) = 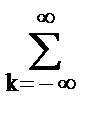 x(k) zk =
x(k) zk =  ak zk =
ak zk =  (az)k.
(az)k.
Как и в предыдущем случае, ряд сходится при |az| < 1, при этом:
X(z) = 1/(1-az), |z| < 1/a.
При использовании символики z-1:
X(z) = z/(z-a), |z| > a.
Комплексная экспонента:
x(k) = exp(jwk), k ≥ 0; x(k) = 0, k < 0.
X(z) = 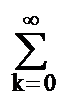 exp(jwk) zk =
exp(jwk) zk = 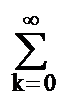 (z exp(jw))k = 1/(1-z exp(jw)), |z| < 1.
(z exp(jw))k = 1/(1-z exp(jw)), |z| < 1.
Аналитическая форма z-образов существует для z-преобразований, если возможно свертывание степенного ряда в аналитическое выражение. Выше, в примерах z-преобразования, уже приводилось приведение к аналитической форме z-образов функции Хевисайда и экспоненциальной функции. Ниже в таблице приводится z-трансформация ряда распространенных функций, которые могут использоваться для прямого и обратного преобразования.
Таблица 8.2.1.
| Функция s(k), k≥0 | z - образ S(z) | z-1 – образ S(z) |
| b | b / (1-z), |z| < 1 | bz / (z-1), |z| > 1 |
| b k | bz / (1-z)2, |z| < 1 | bz / (z-1)2, |z| > 1 |
| b k2 | bz (1+z) / (1-z)3, |z| < 1 | bz (z+1) / (z-1)3, |z| > 1 |
| b ak | b / (1 - za), |z| < 1/a | bz / (z - a), |z| > a |
| bkak | baz / (1 - za)2, |z| < 1/a | baz / (z - a)2, |z| > a |
| cos ak | (1-z cos a) / (1-2z cos a+z2), |z| < 1 | z (z-cos a) / (z2-2z cos a+1), |z| > 1 |
| sin ak | z sin a / (1-2z cos a+z2), |z| < 1 | z sin a / (z2-2z cos a+1), |z| > 1 |
| b exp(-ak) | b / (1-z exp(-a)), |z| < 1/exp(-a) | bz / (z-exp(-a)), |z| > exp(-a) |
| bk exp(-ak) | bz exp(-a) / (1-z exp(-a))2, |z| < 1/exp(-a) | bz exp(-a) / (z-exp(-a))2, |z| > exp(-a) |
В таблице приведены преобразования как для символики z, так и для символики z-1 (по Гуревичу), которая иногда бывает удобней в некоторых математических операциях. Переход из одной символики в другую достаточно прост и выполняется заменой z в одной символике на 1/z в другой.
Дата добавления: 2017-08-01; просмотров: 499;
