Пример разложения периодического сигнала вряд Фурье

Рассмотрим пример представления периодического сигнала суммой элементарных гармоник. Пусть сигнал задан функцией 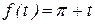на интервале [0,2p]. График данной функции представлен на рис.5.

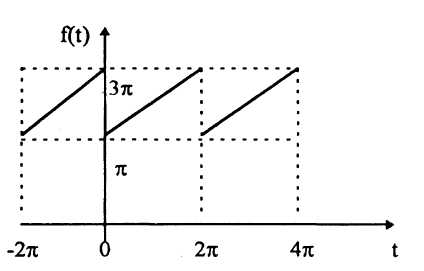
Рис.5. Сложный периодический сигнал

Период функции T=2p. Следовательно, частота

.

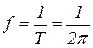Тогда угловая частота

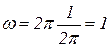
В этом случае разложение функции f(t) в ряд Фурье вида (18) примет следующий вид:

.

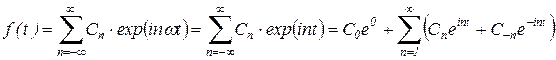(18)

Найдем коэффициенты С₀, С_n и С_-n:

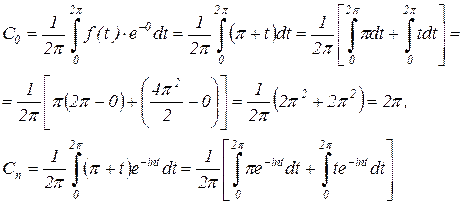
Рассмотрим интегралы в квадратных скобках по отдельности.

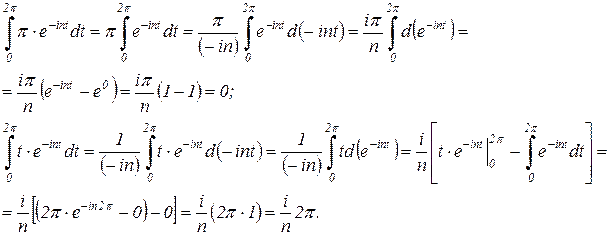
Также можем получить значение коэффициента С_n:

.

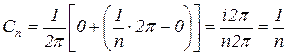Поделав аналогичные вычисления для коэффициента С_-n, получим

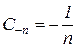
Найдя выводы для C₀, C_n, C_-n, подставив их в выражение разложения функции f(t), получим

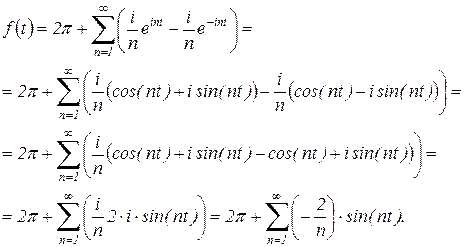
Таким образом получили

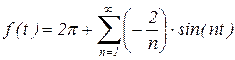
Сложный сигнал, представленный функцией f(t), является суммой простых гармонических сигналов. На рис. 6 представлено приближение функции f(t) суммой гармоник в зависимости от числа приближений n (см. пример 1).

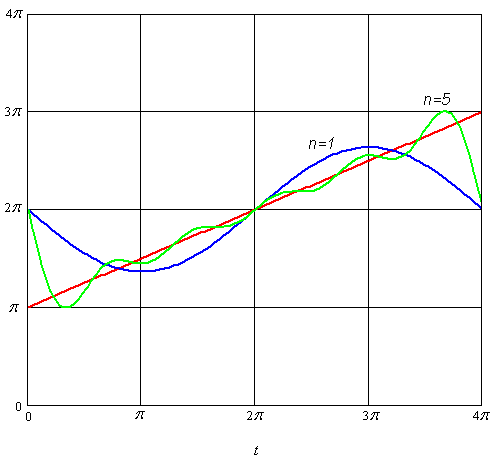
Рис. 6. Приближение функции суммой гармоник в зависимости от числа n

Изменение амплитуды гармонического сигнала в зависимости от номера гармоники n представлено на рис.7.

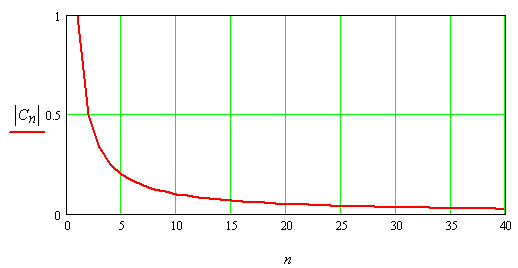
Рис.7. Изменение амплитуды гармонического сигнала

Выводы.

На основе проведенного анализа сложного периодического сигнала можно сделать следующие выводы:

· датчик, установленный в какой-либо точке исследуемой механической системы, измеряет функцию времени в виде

;

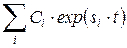· функция времени имеет стандартный вид: ;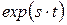

· вибрация механической системы есть суперпозиция гармонических колебаний и затухающих собственных колебаний (с демпфированием);

· любой периодический сигнал может быть представлен в виде суммы простых гармоник.