Уравнение частоты собственных колебаний механической системы.

Любая техническая система в процессе своей эксплуатации подвержена воздействию внешних силовых факторов, которое определяется как входной сигнал. Результатом взаимодействия входного сигнала с технической системой является выходной сигнал. Следовательно, задача исследования технической системы состоит в ответе на вопрос: как входной сигнал преобразуется в выходной сигнал? То есть, возникает необходимость оценки количественных характеристик системы и возможности преобразования входного сигнала.

Исследование состояния системы необходимо начать с представления ее некой расчетной схемой и составления на основе учета действующих на систему сил уравнения ее движения.

В общем случае уравнение движения системы представляет собой дифференциальное уравнение в частных производных второго порядка по времени и четвертого порядка по пространственным координатам относительно функции перемещения точек системы. Исторически одним из первых методов, нашедших широкое применение при решении краевых задач для уравнений с частными производными, является метод разделения переменных, или метод Фурье, заключающийся в построении набора частных решений, каждое из которых разыскивается в виде произведения функций меньшего числа переменных (как правило, одного переменного). В ряде случаев оказывается, что такое представление не вступает в противоречие с исходным дифференциальным уравнением (тогда говорят, что уравнение допускает разделение переменных) и приводит в зависимости от размерности задачи к нескольким дифференциальным уравнениям, содержащим один и тот же числовой параметр. В зависимости от характера области, в которой решается краевая задача, граничных и начальных условий представляется возможным определить дискретные значения (иногда сплошной спектр) этих параметров, что приводит к совокупности частных решений, суммируя которые находят достаточно общее представление решения. Неизвестные коэффициенты (дискретные значения или некоторые функции) определяются уже на заключительном этапе при удовлетворении краевых условий.

В самом общем случае решение дифференциального уравнения движения системы может быть представлено в виде

;

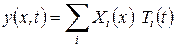(19)

где 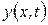- перемещение точек системы;

x - радиус-вектор точки системы;

t - время;

Х_i (х) - функция формы;

T_i (t) - функция времени.

Функция времени T(t) (индекс i опущен) определяется из обыкновенного дифференциального уравнения относительно времени t, и получаемого из общего уравнения движения после разделения переменных. В общем случае уравнение для определения T(t) имеет вид для случая постоянных коэффициентов:

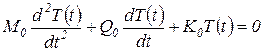
(20)

для случая переменных коэффициентов:

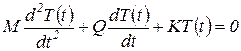
(21)

В (20) и (21) М₀, М - соответственно постоянная и переменная матрицы масс; К₀, К - соответственно постоянная и переменная матрицы жесткости; Q₀, Q - соответственно постоянная и переменная матрицы, иногда называемые матрицей демпфирования, что верно лишь для частных случаев. В общем случае реальная механическая система представляет собой сложную комбинацию одномассовых и многомассовых систем и систем распределенными параметрами. Поэтому коэффициентами в уравнениях (20) и (21) в общем случае являются матрицы.

Из (20) следует, что характеристиками описываемого данным уравнением механического процесса являются спектр собственных чаете (собственных значений) 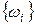и соответствующие им функции форм (собственные функции) Х_i(х). Характеристиками же описываемого уравнением (21) механического процесса являются спектр критических частот изменения параметра и область динамической неустойчивости. При этом спектр критических частот строится на основе спектра собственных частот уравнения с постоянными коэффициентами.

Спектр критических частот, область динамической неустойчивости и анализ уравнения с переменными коэффициентами является самостоятельной задачей, выходящей за рамки данного курса. Поэтому для первого знакомства с основами технической диагностики ограничимся только анализом собственных и вынужденных колебаний систем, уравнения движения которых описываются уравнениями с постоянными коэффициентами, а функция времени в решении (19) находится из уравнения (20).

Уравнение (20) может быть представлено в виде

,

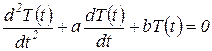(22)

где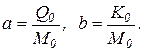

Решение уравнения (22) зависит от соотношения между его коэффициентами. При

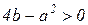
решение будет иметь вид

,

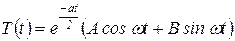(23)

где 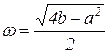- собственная частота.

При

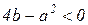
решение имеет вид

,

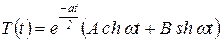(24)

где 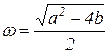- собственная частота.

При 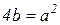решение имеет вид

,

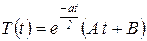(25)

Функция времени (25) представляет собой суперпозицию двух монотонных процессов, численно выраженных экспонентой и линейной функцией времени. То есть, функция (25) не описывает процесса гармонических колебаний системы и поэтому не будет рассматриваться в рамках нашего курса.

Процессы, характеризуемые функцией времени (24), не являются характерными для рассматриваемой нами области техники. Поэтому в рамках нашего курса ограничимся рассмотрением процессов, характеризуемых функцией времени (23).

Согласно (23) функция времени зависит от угловой собственной частоты w, это означает, что частоты собственных колебаний системы, а следовательно, в более общем случае спектр собственных частот системы являются численными характеристиками, количественно отражающими состояние системы. В свою очередь, значение частоты зависит от массы, демпфирования и жесткости механической системы. Изменение любого параметра системы, количественно влияющего на эти матрицы, ведет к изменению частоты собственных колебаний, а следовательно, и к изменению функции времени.

Но влияние частоты не ограничивается только функцией времени. Покажем, что выражение каждой из функций формы в (19) зависит от соответствующего ей значения собственной частоты.