Комплексное частотное решение для свободных колебаний механической системы с демпфированием

Есть два пути диагностического анализа технического объекта (системы):

· измерение входного и выходного сигналов с последующей их статистической обработкой с целью установления какой-либо закономерности между ними (модель "черного ящика");

· представление технической системы в виде некоторой модели с формальным описанием ее состояния аналитическим уравнением движения.

Аналитическое решение обладает огромным преимуществом, ибо позволяет оценить функциональную зависимость всех участвующих в процессе параметров. В результате удается проанализировать процесс движения технической системы (например, по принципу анализа функций в математике) применительно к задачам технической диагностики. Но аналитическое решение обладает и недостатками, способными привести к принципиальной ошибке или даже свести на нет полученный результат.

Поиск аналитического решения требует точного знания всех параметров, так или иначе влияющих на процесс движения механической системы (насосов, компрессоров, трубопроводных систем и т.д.). Учитывая, что, как минимум, значительная часть таких параметров имеет случайный характер с широким диапазоном изменения своего численного значения, получение точного аналитического или численного (на ЭВМ) решения задачи и его использование требует большой аккуратности и высокой квалификации, ибо вероятность ошибки огромна.

Проанализируем путь измерения входного и выходного сигналов (модель "черного ящика"). В данном случае мы не связаны необходимостью точного знания всех влияющих на механический процесс параметров, ибо измеряя ту или иную характеристику получаем конечный результат совместного действия на техническую систему всех участвующих в процессе движения системы факторов. Но измерение какого-либо параметра отнюдь не ведет еще к полному решению задачи. Проведение измерений и их точность являются принципиальным этапом решения задачи. Но еще более важным является этап обработ ки полученных результатов. Для выявления причин возможного изменения состояния системы необходимо знать функциональные связи между большим числом факторов.

По-видимому, наиболее перспективным является метод сочетания аналитического решения с измерением, который позволяет использовать при качественной оценке состояния механической системы ее истинные количественные характеристики. Аналитическое решение необходимо именно для расшифровки поступающего сигнала. В противном случае следует проводить статистическую обработку, для которой необходима исходная модель и достаточное количество измерений. Именно на основании анализа аналитического решения можно получить модель статистической обработки и, следовательно, информацию о том, как проводить измерения.

Уравнение движения системы в большинстве случаев является дифференциальным уравнением 4-го порядка по пространственным координатам и 2-го по времени, решение которого имеет вид

где у - исследуемая численная характеристика механической системы (например, перемещение, скорость, ускорение точек системы);

х - радиус-вектор точки системы, х= {х1, х2, х3};

t - время;

f(x,t) - закон изменения параметров системы, который нужно найти.

В большинстве случаев решение (1) уравнения движения допускает разделение переменных (метод разделения переменных Фурье). В этом случае искомое решение ищется в виде

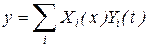
(2)

где 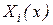- искомая функция формы;

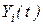- искомая функция времени.

В результате подстановки решения (2) в уравнение движения (1) вместо одного уравнения относительно двух переменных х и t имеем два уравнения относительно соответственно одного переменного х и t.

Рассмотрим возможность определения параметров закона системы путем измерения, При этом прежде всего необходимо установить: что за сигнал поступает на датчик и как из этого сигнала получить информацию о состоянии системы?

Согласно принципу разделения переменных общее искомое решение уравнения движения системы может быть представлен в виде (2). Но датчик стоит в конкретной точке, то есть координаты данной точки фиксированы, что математически означает х = х⁰. В этом случае выражение (2) имеет вид

(3)

где C_i - постоянные.

Таким образом, измеряя параметры механической системы в конкретной точке мы измеряем функцию времени закона изменения параметров механической системы (2). При этом искомая функция времени является согласно (3) суммой (линейной комбинацией) неких функций времени. Это значит, что вопрос нахождения и исследования искомой функции времени (3) в данной точке механической системы является фактически вопросом нахождения и исследования функций, составляющих ее линейную комбинацию. Поэтому не ограничивая общности рассуждений, рассмотрим некую отдельную функцию времени y(t), входящую в линейную комбинацию (3) или являющуюся ее результатом. Что представляет собой выражение (3) в чисто механическом аспекте? Фактически мы сводим рассматриваемую систему к некой одномассовой (рис.1), закон изменения параметров которой тождественно равен закону изменения параметров исследуемой системы в данной точке.

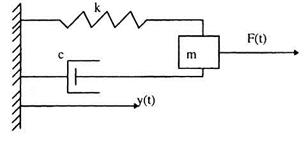
Рис.1. Одномассовая механическая система

Уравнение движения одномассовой механической системы имеет вид\

,

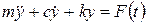(4)

где 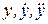- перемещение, скорость и ускорение одномассовой сисметы;

m - масса системы;

с - коэффициент демпфирования;

к - жесткость системы;

F(t) - внешняя возбуждающая сила, действующая на систему.

В случае свободных колебаний (внешняя возбуждающая сила F(t)=0) уравнение (4) имеет вид

,

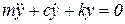(5)

Общее решение уравнения (5) есть

,

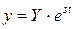(6)

Искомое решение в данном виде подставляем в уравнение (5) и приходим к алгебраическому уравнению

,

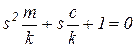(7)

которое называется характеристическим уравнением системы. Обозначим собственную частоту системы без демпфирования

,

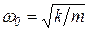и, подставив в уравнение (7), получим

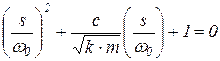
(8)

или

,

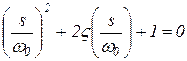(9)

где 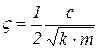является относительным демпфированием.

Корни квадратно уравнения (9) будут

.

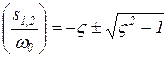(10)

При 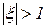корни являются действительными величинами, в противном случае - комплексными. В этом случае корень s = s + i w называется комплексной частотой. Эти частоты графически изображаются в плоскости комплексной частоты, в которой вещественная ось представляет собой s, скорость затухания (величину демпфирования), а мнимая ось представляет величину i w - угловую частоту (рис.2). Каждая точка на этой плоскости определяет некоторую форму колебаний. Если величина s является чисто мнимой, то решение уравнения имеет вид

.

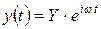(11)

и характеризует колебания с постоянной амплитудой.

При чисто вещественном значении s решение имеет вид

.

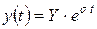что соответствует неколебательному движению.

Значения s, являющиеся комплексными и, следовательно, лежащие на плоскости и дающие решения в виде

.

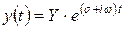описывают колебательное движение, амплитуда которого увеличивается или уменьшается экспоненциально во времени в зависимости от знака s.

Таким образом, колебательное и неколебательное движения могут рассматриваться по отдельности. Корректность такого подхода обеспечивается принципом суперпозиции сил.

Учитывая, что закон изменения параметров системы формально характеризуется функцией времени y(t), приведем основные термины и определения.

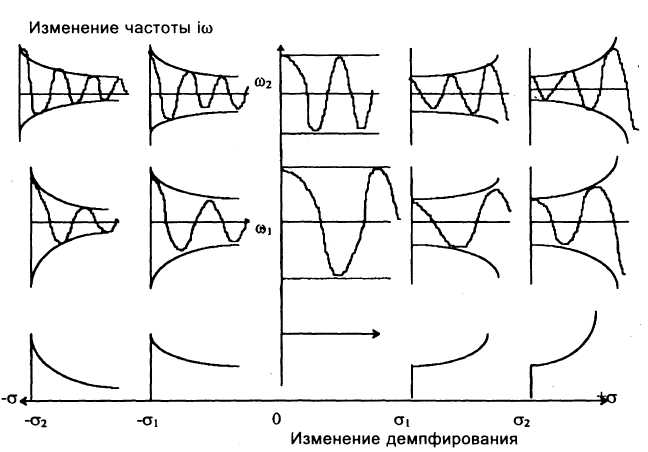
Рис.2. Колебания, соответствующие точкам на комплексной плоскости

Колебания (вибрация), при которых значения колеблющейся величины (характеризующей вибрацию) изменяются во времени по закону

,

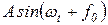(12)

где А - амплитуда, 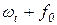- фаза, 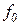- начальная фаза, 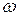- угловая частота;

A, 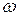, 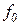- постоянные параметры, называются гармоническими колебаниями (вибрацией).

Максимальное значение величины (характеризующей вибрацию) при гармонических колебаниях (вибрации) называется амплитудой гармонических колебаний (вибрации). Амплитудой.

Аргумент синуса, которому пропорционально значение колеблющейся величины (характеризующей вибрацию) при гармонических колебаниях (вибрации), называется фазой гармонических колебаний (вибрации). Фазой.

Фаза гаромнических колебаний (вибрации) в начальный момент времени называется начальной фазой гармонических колебаний (вибрации). Начальной фазой.

Колебания (вибрация), при которых каждое значение колеблющейся величины (характеризующей вибрацию) повторяется через равные интервалы времени, называются периодическими колебаниями (вибрацией).

Наименьший интервал времени, через который при периодических колебаниях (вибрации) повторяется каждое значение колеблющейся величины (характеризующей вибрацию), называется периодом колебаний (вибрации). Периодом.

Величина, обратная периоду колебаний (вибрации), называется частотой периодических колебаний (вибрации). Частотой.

Производная по времени от фазы гармонических колебаний (вибрации), равная частоте, умноженной на 2 я, называется угловой частотой гармонических колебаний (вибрации). Угловой частотой.

Комплексная величина, модуль которой равен амплитуде, а аргумент - начальной фазе гармонических колебаний A exp(if), называется комплексной амплитудой гармонических колебаний. Комплексной амплитудой.

Таким образом, можно констатировать, что:

датчик, установленный в какой-либо точке исследуемой механической системы, измеряет функцию времени в виде

,

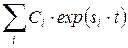функция времени имеет стандартный вид: exp(st); вибрация механической системы есть суперпозиция гармонических колебаний и затухающих (с демпфированием).