Метод валентных связей (ВС)
Основы метода ВС разработали в 1927 г. Вальтер Гайтлер (Heitler) и Фриц Лондон (London). Модельной частицей для этого метода является молекула водорода Н2. При построении волновой функции молекулы в методе валентных связей считается, что: 1)атомы в молекуле сохраняют свою индивидуальность – каждый электрон принадлежит ядру своего атома, 2) известны волновые функции электронов атома А (YА) и атома В (YВ) –атомные орбитали, 3) считается, что частицы (электроны и ядра атомов) неразличимы.
Уравнение Шрёдингера для молекулы водорода. Составим уравнение Шрёдингера для молекулы водорода. Входящая в него потенциальная энергия включает в себя сумму энергий электростатического взаимодействия всех частиц между собой (двух электронов -e и двух ядер +e). Из рис. 3.3 видно, что суммарная потенциальная энергия складывается из двух положительных членов: энергии отталкивания электронов и ядер между собой и четырех отрицательных – энергий притяжения электронов к ядрам:
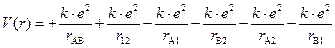 ,
,
 где rAB; r12 − расстояния между ядрами атомов А и В и между первым и вторым электронами; rA1; rA2 – расстояния между ядром атома А и первым и вторым электронами соответственно; rB1; rB2 – расстояния между ядром атома В и первым и вторым электронами соответственно.
где rAB; r12 − расстояния между ядрами атомов А и В и между первым и вторым электронами; rA1; rA2 – расстояния между ядром атома А и первым и вторым электронами соответственно; rB1; rB2 – расстояния между ядром атома В и первым и вторым электронами соответственно.
Рис. 3‑3 Схема электростатического взаимодействия электронов и ядер в молекуле водорода
Таким образом, уравнение Шрёдингера для молекулы водорода имеет вид
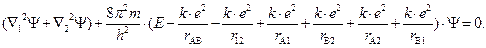
Аналитическое решение данного уравнения практически невозможно, поэтому нахождение энергии химической связи DE(r) и волновой функции электронов, показывающей распределение электронной плотности в молекуле, производят приближенным методом.
Функция первого приближения. Поскольку вероятность нахождения электрона в элементарном объеме пропорциональна Y-функции, а по условиям метода ВС атомы при образовании связи сохраняют свои атомные орбитали, то в первом приближении функция, описывающая состояние электронов в молекуле водорода, может быть представлена как произведение волновых функций электронов в отдельных изолированных атомах водорода:
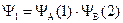 ,
,
где Y1 – функция, описывающая состояния электронов в молекуле водорода; YА(1) – функция, описывающая состояния электрона 1, принадлежащего атому А (Y1s – функция основного состояния атома водорода); YВ(2) функция, описывающая состояния электрона 2, принадлежащего атому В (Y1s).
Поскольку электроны и ядра атомов принципиально неразличимы, то безразлично, какой из них будет находиться у определенного ядра. Поэтому необходимо составить и вторую функцию:
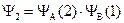 .
.
Первая функция рассматривает 1 электрон как принадлежащий атому А, а 2 – атому В, вторая функция, наоборот, считает, что 2 электрон принадлежит атому А, а 1 – атому В. Обе функции являются решениями уравнения Шрёдингера. Для простоты изложения нормировочные множители приняты равными единице.
Расчет с использованием этих функций качественно правильно описывал молекулу водорода, но величины энергии и длины связи сильно отличались от величин, определенных экспериментально.
Более точным приближением к истинной волновой функции явилась линейная комбинация первой и второй функции:
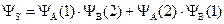 ,
,
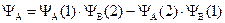 .
.
Физический смысл этих двух функций заключается в следующем: YS – симметричная функция – соответствует случаю, когда электроны в молекуле водорода имеют разные по знаку значения спинового квантового числа, – спины электронов антипараллельны. YА – антисимметричная функция – описывает состояние, когда оба электрона имеют одинаковое значение спинового числа – спины электронов параллельны.
Изменение энергии системы двух взаимодействующих атомов водорода описывается выражением
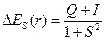 – для симметричной функции,
– для симметричной функции,
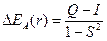 – для антисимметричной функции,
– для антисимметричной функции,
Q – «кулоновский интеграл», характеризующий изменение энергии системы вследствие электростатического взаимодействия электронов и ядер между собой. I – «обменный интеграл», интеграл, характеризующий понижение энергии системы вследствие неразличимости электронов; S – «интеграл перекрывания», характеризующий изменение энергии системы вследствие перекрывания атомных орбиталей.
Для выяснения физического смысла этих интегралов проанализируем их выражения.
«Интеграл перекрывания»
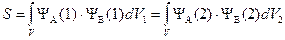
характеризует область пространства перекрывания атомных орбиталей.
«Кулоновский интеграл»
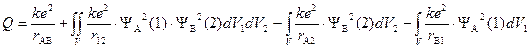
показывает изменение энергии системы в результате отталкивания ядер друг от друга (первый член суммы), электронов (второй член) и притяжения электронов к ядрам «несвоего атома» (третий и четвертый члены). Последние два интеграла равны между собой, поскольку атомы одинаковы. Физический смысл интегралов очевиден: yi2dVj – вероятность нахождения j-электрона в элементарном объеме пространства, e×yi2dVj – величина заряда. Согласно закону Кулона энергия электростатического взаимодействия прямо пропорциональна произведению величины зарядов и обратно пропорциональна расстоянию между ними.
Энергия притяжения электронов к ядрам «своего атома» – энергия невзаимодействующих атомов (E0) – в энергии химической связи не учитывается (полная энергия молекулы водорода E = 2×E0+DE(r)).
«Обменный интеграл»
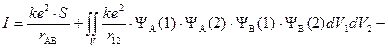
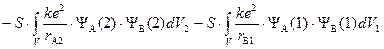 ,
,
S – «интеграл перекрывания».
«Обменный интеграл» похож на «кулоновский», но вместо квадрата волновой функции для данного электрона стоит произведение волновых функций разных атомов, что придает ему достаточно абстрактный характер - «неклассическое электростатическое взаимодействие». Энергия системы изменяется вследствие неразличимости электронов, то есть возможность замены одного электрона на другой приводит к изменению энергии системы.
На расстояниях r®¥ кулоновский, обменный интегралы и интеграл перекрывания стремятся к нулю: Q®0, I®0 и S®0. На расстояниях, близких к длине связи, кулоновский и обменный интегралы отрицательны Q<0; I<0, причем ½Q½<½I½; при r®0 они становятся положительными. Интеграл перекрывания всегда положителен и меньше единицы: 0£S<1.
В случае симметричной функции (спины электронов антипараллельны) в зависимости DE(r) существует минимум (потенциальная яма), а электронная плотность между атомами возрастает – химическая связь образуется, молекула устойчива (рис. 3.4).
 | |||
| |||
Рис. 3‑4 Зависимость изменения энергии молекулы и распределение электронной плотности в молекуле водорода в случае описания системы симметричной (YS) и антисимметричной функцией (YA)
В случае антисимметричной функции (спины электронов параллельны) минимум в зависимости DE(r) отсутствует, электронная плотность между ядрами равна нулю – связь не образуется.
Пример. Энергия и длина связи в молекуле водорода, определенные экспериментально и рассчитанные с учетом различных факторов, усложняющих явный вид волновых функций:
| Энергия связи, эВ | Длина связи, Ǻ | |
| Эксперимент…………………….. | 4,747 | 0,741 |
| Функции Y1s×Y1s………………… | 0,25 | 0,9 |
| Функции YS YA………………….. | 3,14 | 0,869 |
| С учетом сжимаемости атомов… | 3,76 | 0,743 |
| С учетом поляризации атомов…. | 4,02 | 0,749 |
| С учетом ионности связи……….. | 4,10 | 0,740 |
На основе представлений, выработанных при расчете молекулы водорода, сформулированы основные принципы (постулаты) метода валентных связей, позволяющие описывать образование ковалентной химической связи в более сложных молекулах:
1. Единичная химическая связь образуется общей парой электронов с противоположными (антипараллельными) спинами.
2. Общая электронная пара локализована (сосредоточена) между атомами в направлении максимального перекрывания атомных орбиталей.
3. Энергия связи определяется только силами электростатического взаимодействия электронов и ядер и зависит от величины перекрывания орбиталей.
Таким образом, число связей (валентность), которые может образовывать атом, определяется числом неспаренных электронов на внешнем энергетическом уровне атома в основном или возбужденном состоянии. Ковалентная связь обладает свойством насыщенности (атом может образовывать ограниченное число единичных ковалентных связей). Ковалентная химическая связь обладает свойством направленности (расположение в пространстве общей электронной пары определяется пространственной ориентацией перекрывающихся валентных орбиталей). Атомы взаимно располагаются таким образом, чтобы перекрывание валентных орбиталей было максимальным. Из двух связей та прочнее, где перекрывание валентных орбиталей больше.
Дата добавления: 2017-02-20; просмотров: 1395;
