Степень подвижности механизмов
Составив кинематическую схему механизма и определив число подвижных звеньев, число и типы кинематических пар, необходимо определить степень подвижности механизма.
Подвижность кинематической цепи – это определенность движения звеньев по отношению к одному из них – неподвижному звену, именуемому стойкой. Определенность движения звеньев предполагает строгую повторяемость их траекторий движения и является обязательным свойством кинематической цепи любого реального устройства, так как в противном случае управление устройством невозможно.
За обобщенную координату в плоских механизмах, как правило, принимают угол поворота входного звена φ и следовательно, если задавать ее изменение во времени, то можно получить вполне определенное движение звеньев такой кинематической цепи, называемой механизмом. Таким образом, количество входных звеньев определяется степенью подвижности механизма.
Понятие о степенях подвижности относится не к реальным механизмам, а к их идеализированным моделям. Идеализация состоит в том, что звенья механизма, являющиеся твёрдыми телами, считают абсолютно твёрдыми, жидкие звенья – несжимаемыми, гибкие – нерастяжимыми. Соединения звеньев (кинематические пары) также принимают идеальными (отсутствие зазоров в шарнирах, качение без скольжения во фрикционных передачах и т.п.). Для такого идеального механизма понятие «степень подвижности» равносильно принятому в теоретической механике понятию «число степенейсвободы». (Числом степеней свободы является число независимых параметров, однозначно определяющих положение всех звеньев механизма в пространстве либо на плоскости).
Степень подвижности плоских механизмов определяется по формуле П.Л. Чебышева:
W = 3·n – 2·p5 – p4 (2)
где: W – степень подвижности механизма;
n – число подвижных звеньев механизма;
Р5 – число кинематических пар пятого класса;
Р4 – число кинематических пар четвёртого класса.
В кривошипно-ползунном механизме (Рис. 5) три подвижных звена:кривошип – 2, шатун – 3, ползун – 4 и три кинематические пары пятого класса: вращательные – О(1-2), А(2-3), В(3-4), и поступательная пара В*(4-1) т.е.n=3;Р5=4;Р4=0.
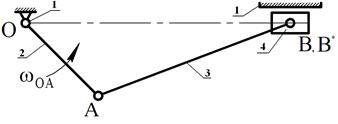
Рис.5 Схема кривошипно-ползунного механизма.
По формуле (1) получаем: W=l. В данном механизме одно входное звено.
1.8 Структурная классификация механизмов
Структурной классификацией механизмов называется разделение их на группы и классы по общности структуры.
Впервые научно обоснованная, рациональная классификация плоских механизмов была предложена в 1914 году русским учёным Л.В. Ассуром. Дальнейшее развитие структурная классификация плоских механизмов получила в работах И.И. Артоболевского.
Классификация механизмов по Ассуру-Артоболевскому позволяет для механизмов, отнесённых к одному и тому же классу, применять методику кинематического и силового анализа, разработанную специально для этого класса механизмов.
Согласно этой классификации, механизм может быть образован путём присоединения к начальному звену (или начальным звеньям) и стойке некоторых кинематических цепей.
Каждое начальное звено, входящее в кинематическую пару со стойкой (вращательную или поступательную) условно называют начальным механизмом. Начальный механизм принято считать механизмом первого класса и первого порядка.
Примерами начальных механизмов являются механизмы электродвигателей и генераторов, центробежных насосов, вентиляторов молотов, гидро – и пневмоцилиндров.
Кинематические цепи, обладающие нулевой подвижностью относительно внешних кинематических пар и не распадающиеся на более простые цепи, удовлетворяющие этому условию, называются структурными группами Ассура.
Структурные группы Ассура не влияют на подвижность механизма, они изменяют его структуру и законы движения звеньев.
В группы Ассура входят только низшие кинематические пары, поэтому степень подвижности группы определится по формуле:
W = 3·n - 2·р5 = 0. (3)
Отсюда следует, что зависимость числа кинематических пар Р5 от числа звеньев n имеет вид:
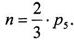 (4)
(4)
Чтобы из механизма выделить структурные группы, необходимо помнить их основные признаки, вытекающие из определения:
а) число звеньев в группе Ассура должно быть чётным, а число кинематических пар кратно трём, (Табл.3)
Таблица 3. Соотношение числа звеньев и числа кинематических пар в группах Ассура
| n | … | |||
| р5 | ... |
б) степень подвижности группы всегда равна нулю;
в) степень подвижности оставшейся части механизма при отсоединении групп Ассура не должна изменяться.
Дата добавления: 2018-03-01; просмотров: 11232;
