Виды зубчатых механизмов
Зубчатый механизм, составленный из зубчатых колес с неподвижными осями, называется зубчатым рядом.
Зубчатый ряд, состоящий из двух колес и стойки, есть рядовая передача.
Внешнее зацепление Внутреннее зацепление
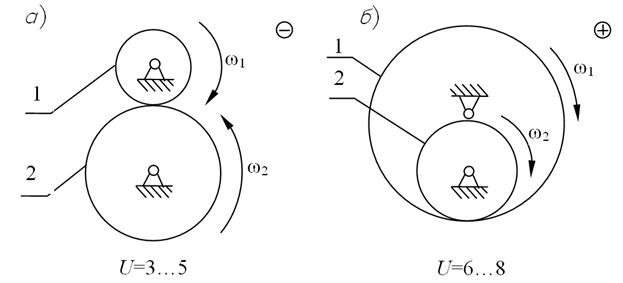
Значение передаточного отношения рядовой передачи обратно пропорционально числу зубьев колес:
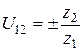 .
.
Знак перед дробью позволяет учесть направление вращения колес. Для внешнего зацепления принят знак (-), учитывающий противоположность вращения колес. Для внутреннего зацепления принят знак (+).
Передаточное отношение любого зубчатого ряда равно произведению передаточных отношений всех передач, входящих в него:
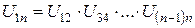 ,
,
где 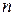 – число колес зубчатого ряда.
– число колес зубчатого ряда.
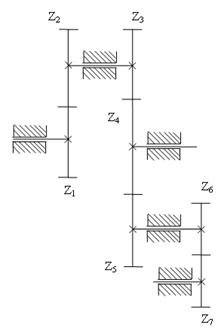 Пример. Дана схема зубчатого ряда. Числа зубьев колес известны
Пример. Дана схема зубчатого ряда. Числа зубьев колес известны 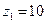 ;
; 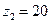 ;
; 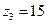 ;
; 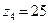 ;
; 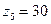 ;
; 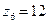 ;
; 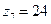 .
.
Определить передаточное отношение 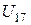 .
.
Зубчатый ряд (рис. 3) состоит из 4-ех передач: 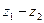 ;
; 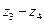 ;
; 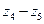 ;
; 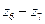 .
.
Общее передаточное отношение механизма равно:
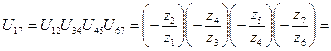
= 
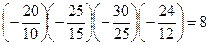
Колесо 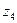 называется промежуточным. Оно не влияет на величину передаточного отношения, но меняет направление вращения.
называется промежуточным. Оно не влияет на величину передаточного отношения, но меняет направление вращения.
Зубчатый механизм, в состав которого входят зубчатые колеса с геометрически подвижной осью называются планетарным механизмом.
 В состав планетарного механизма входят звенья:
В состав планетарного механизма входят звенья:
Сателлиты - зубчатые колеса с геометрически подвижной осью;
Водило - подвижное звено, в котором помещена ось сателлита;
Солнечное колесо - подвижное центральное зубчатое колесо;
Опорное колесо (эпицикл) - неподвижное центральное зубчатое колесо;
Геометрическая ось центральных колес и водила общая.
Для обеспечения этого используют условие соосности
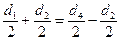 или
или 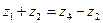
Определение пердаточного отношения планетарной передачи
При исследовании кинематики планетарных передач широко используют метод остановки водила — метод Виллиса.
Всей планетарной передаче мысленно сообщается вращение с частотой вращения водила, но в обратном направлении. При этом водило, как бы затормаживается, а все другие звенья освобождаются. Получаем так называемый обращенный механизм, представляющий собой простую передачу, в которой движение передается от z1 к z4 через паразитные колеса z2. Частоты вращения зубчатых колес обращенного механизма равны разности прежних частот вращения и частоты вращения водила.
Для исследуемого механизма 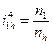
Для обращенного механизма: 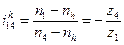
В нашем случае колесо 4 заторможено, 1 ‑ ведущее и h ‑ ведомое, при 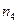 = 0получаем:
= 0получаем:
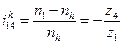 ;
; 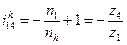
Или 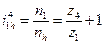
Дата добавления: 2018-11-25; просмотров: 1967;
