Геометрические характеристики сечений.

Детали механизмов и машин отличаются друг от друга по форме и размерам. При расчета на прочность деталей механизмов и машин используются поперечные сечения деталей, имеющие свои геометричекие характеристики.

Рассмотрим геометричекие характеристики плоских сечений.

Площадь -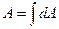

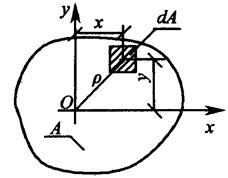
Статический момент относительно оси 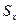, 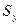– сумма произведений площадей элементарных площадок 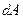на их расстояния до этой оси.

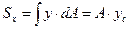
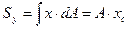
где 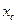, - расстояния от центра тяжести данного сечения до осей x и y соответственно.

Статический момент сложного сечения относительно некоторой оси равен сумме статических моментов всех частей этого сечения относительно той же оси:

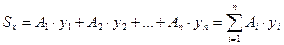
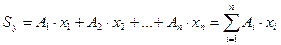
где 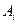- площади фигур, составляющих плоское сечение

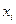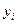, - расстояния от центров тяжести фигур до осей x и y соответственно.

Последнее выражение позволяет определить положение центра тяжести для любого составного сечения

Пример

Определить положение центра тяжести сечения показанного на рисунке.

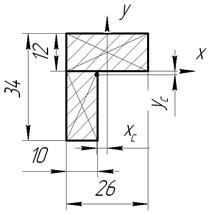
Проводим оси x и y и разбиваем сечение на простые фигуры (два прямоугольника).

Определяем площади фигур

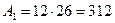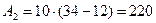мм²; мм²;

Находим расстояние от цениров тяжестей фигур до осей

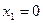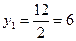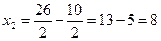; мм; 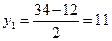мм; мм

Записываем выражение для статических моментов инерции

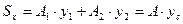
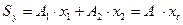
Отсюда

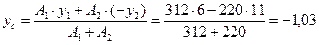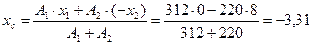мм

мм

Осевой момент инерции относительно оси сумма произведений площадей элементарных площадок 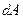на квадраты их расстояний до этой оси.

;

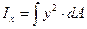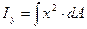
Полярный момент инерции плоского сечения относительно некоторой точки (полюса) О сумма произведений элементарных площадок dA на квадраты их расстояний от этой точки, т.е.

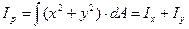
Пример

Определить осевые и полярный моменты инерции прямоугольника высотой h и шириной b относительно осей х и у

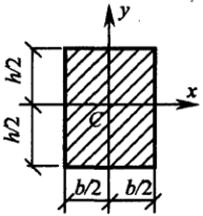Представим 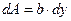, тогда

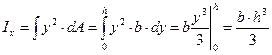
Представим 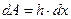, тогда

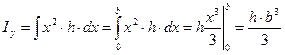
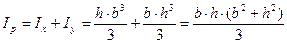
Осевой момент сопротивления относительно оси – отношение осевого момента инерции к расстоянию от наиболее удаленной точки сечения по этой оси

;

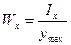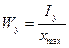
Полярный момент сопротивления относительно точки (полюса) – отношение полярного момента инерции к расстоянию от наиболее удаленной точки сечения до полюса

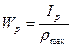
Пример

Для предыдущего примера определить осевые и полярные моменты сопротивления

;

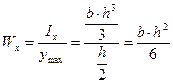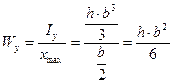
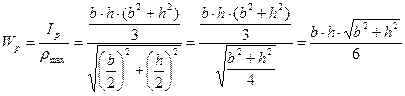
Для основных сечений формулы для расчета геометрических характеристик приводятся в технических справочниках.

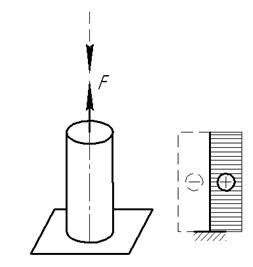
Виды нагружения.

Растяжение-сжатие.

При воздействии на тело силы, линия действия которой проходит по оси данного тела, в поперечном сечении (перпендикулярном линии действия силы) возникают напряжения, называемые напряжениями растяжения или сжатия, в зависимости от направления действия силы.

В случае растяжения-сжатия прочность тела оценивается по формуле

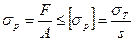
где 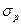- действительные напряжения растяжения (сжатия);

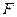- сила, действующая на тело;

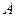- площадь поперечного сечения тела;

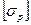- допускаемые напряжения растяжения (сжатия);

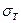- предел текучести материала;

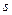- коэффициент запаса прочности

Для удобства представления информации на расчетной схеме напряжения представляются в виде эпюр.

Эпюра – группа условных линий, показывающих величину и направление напряжений, возникающих в рассматриваемом теле.

Если по длине тела изменяются размеры поперечного сечения или приложенная нагрузка, то изменятся и величина напряжений

Пример

Построить эпюры напряжений для бруса, изображенного на рисунке.

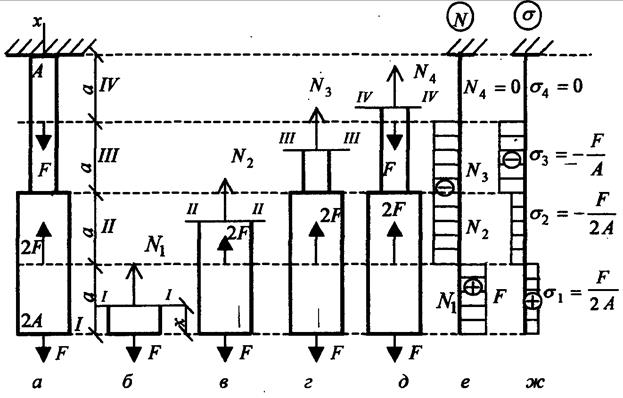
Решение. Для определения внутренних усилий разбиваем прямолинейный брус на участки. Границами участков являются точки продольной оси, соответствующие изменению площади поперечного сечения и точкам приложения сосредоточенных сил.

Проводим сечение I-I. Отбросим верхнюю часть бруса, ее действие заменим нормальной силой 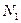. Запишем уравнение равновесия, проектируя силы на ось бруса:

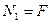
Определим напряжения на участке I:

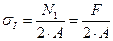
Проводим сечение II-II. Отбросим верхнюю часть бруса, ее действие заменим нормальной силой 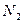. Запишем уравнение равновесия, проектируя силы на ось бруса:

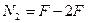
Определим напряжения на участке II:

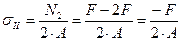
Проводим сечение III-III. Отбросим верхнюю часть бруса, ее действие заменим нормальной силой 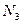. Запишем уравнение равновесия, проектируя силы на ось бруса:

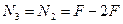
Определим напряжения на участке III:

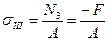
Проводим сечение IV-IV. Отбросим верхнюю часть бруса, ее действие заменим нормальной силой 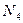. Запишем уравнение равновесия, проектируя силы на ось бруса:

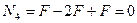
Определим напряжения на участке IV: