Арифметический корень. Степень с рациональным показателем.
1º. Арифметическим корнем k-ой степени ( 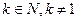 ) из числа а ≥ 0 называется неотрицательное число b, k-ая степень которого равна а:
) из числа а ≥ 0 называется неотрицательное число b, k-ая степень которого равна а:

2º. Замечание. Для любого действительного числа а, любого натурального числа n действуют правила:
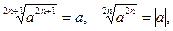 в частности
в частности 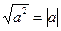 .
.
3º. Свойства арифметических корней. Пусть 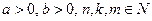 . Тогда:
. Тогда:
1) 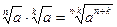 ; 2)
; 2) 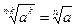 ; 3)
; 3) 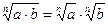 ;
;
4) 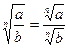 ; 5)
; 5) 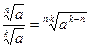 ; 6)
; 6) 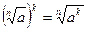 ;
;
7) 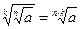 .
.
4º. Степенью числа a с рациональным показателем 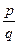 определяется равенством:
определяется равенством:
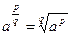
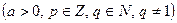
Степень с рациональным показателем обладает теми же свойствами, что и степень с целым показателем.
Пример 7. Упростить выражение: 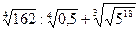 .
.
Решение. Используя определение степени и ее свойства, получим:
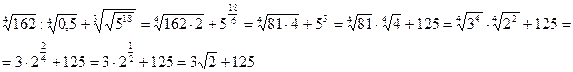
Формулы сокращенного умножения.
1º. Во всякого рода алгебраических преобразованиях используются формулы сокращенного умножения:
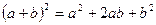 ;
; 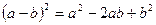 ;
;
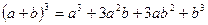 ;
; 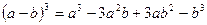 ;
;
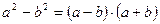 ;
;
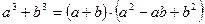 ;
; 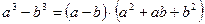 .
.
Так, если а ≥ 0, b ≥ 0, то 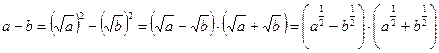 .
.
Или 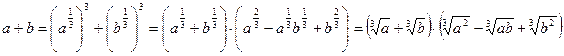 .
.
Пример 8. Вычислить 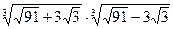 .
.
Решение:
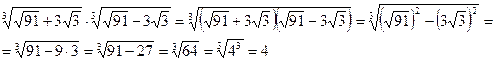
Ответ: 4.
Дидактический материал.
Вычислите:
1. 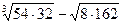 ; 2.
; 2. 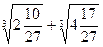 ; 3.
; 3. 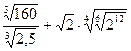 ;
;
4. 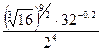 ; 5.
; 5. 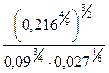 ; 6.
; 6. 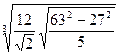 ;
;
7. 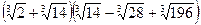 ; 8.
; 8. 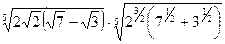 ;
;
9. 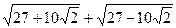 ; 10.
; 10. 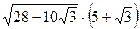 ;
;
11. 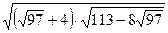 ; 12.
; 12. 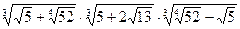 ;
;
13. 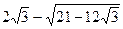 ; 14.
; 14. 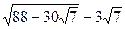 ; 15.
; 15. 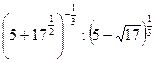 .
.
Внесите множители под знак общего корня:
16. 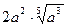 ; 17.
; 17. 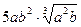 ; 18.
; 18. 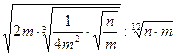 .
.
Упростите выражения:
19. 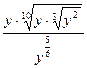 ; 20.
; 20. 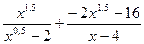 ; 21.
; 21. 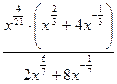 ;
;
22. 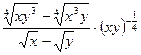 ; 23.
; 23. 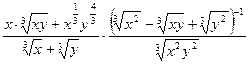 ;
;
24. 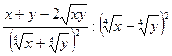 ; 25.
; 25. 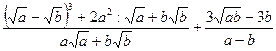 ;
;
26. 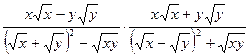 ;
;
27. 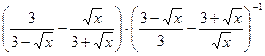 .
.
Ответы: 19. 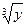 ; 20. x + 4; 21. 0,5; 22. -1; 23.
; 20. x + 4; 21. 0,5; 22. -1; 23. 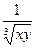 ; 24. 1; 25. 3; 26. x – y;
; 24. 1; 25. 3; 26. x – y;
27. 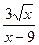 .
.
Тема №4.
Неравенства с одной переменной (часть I).
Дата добавления: 2017-09-19; просмотров: 449;
