Действие вибрационной силы на систему с одной степенью свободы

При действии на систему с одной степенью свободы вибрационной силы 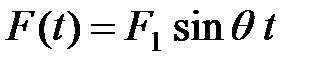уравнение движения (1.8) запишем в виде:

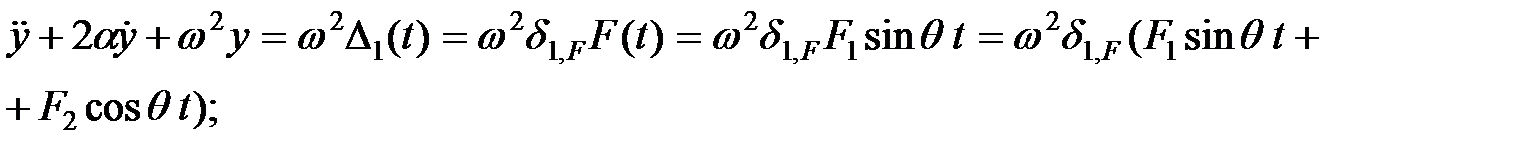
(1.24)

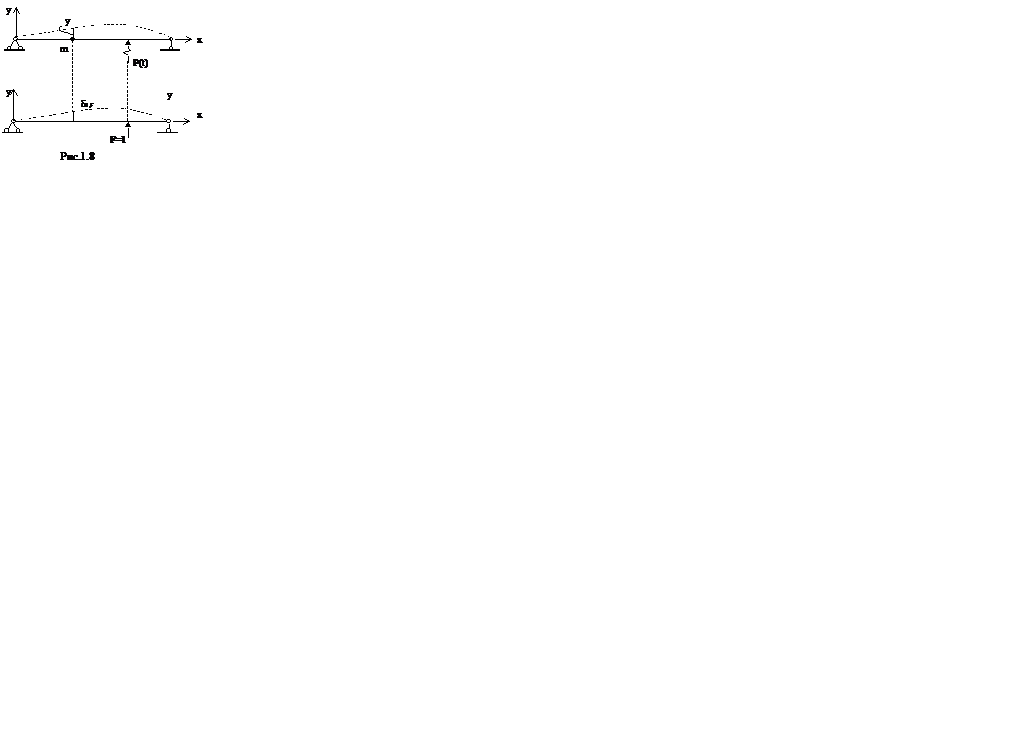
В формуле (1.24) 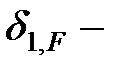перемещение точки присоединения массы под действием статической силы F₁=1 (см. рис.1.8). Слагаемое 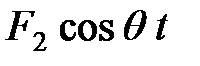введено для удобства решения уравнения; в окончательных результатах положим F₂=0.

Уравнение (1.24) решается следующим образом.

Запишем частное решение в виде:

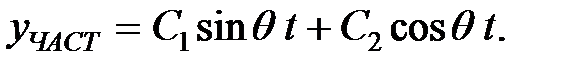
(1.25)

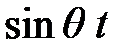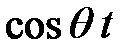Подставим у_част и его производные в уравнение (1.24) и приравняем коэффициенты при и в левой и правой частях. Получим:

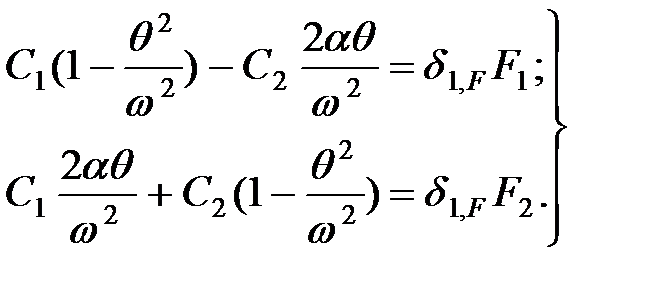
(1.26)

Определяя С₁ и С₂, подставляя их в уравнение (1.25) и приравнивая F₂ нулю, получаем:

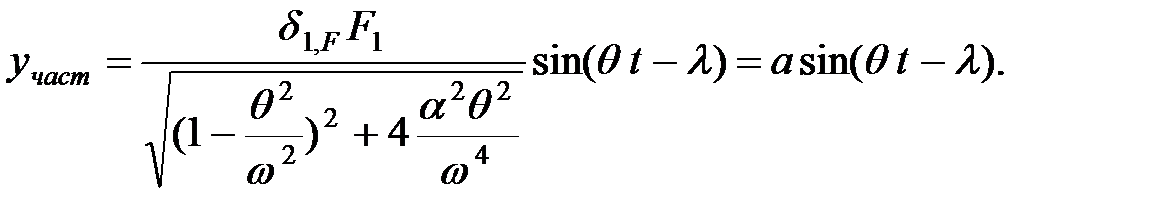
(1.27)

В формуле (1.27)

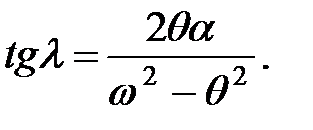
Кроме того, принято обозначение

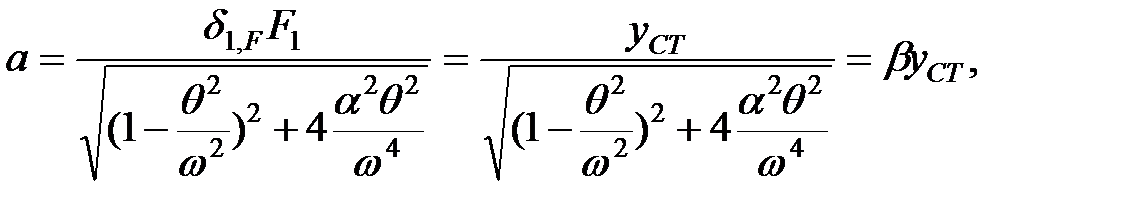
(1.28)

где коэффициент 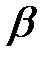, называемый амплитудным динамическим коэффициентом, определяется равенством:

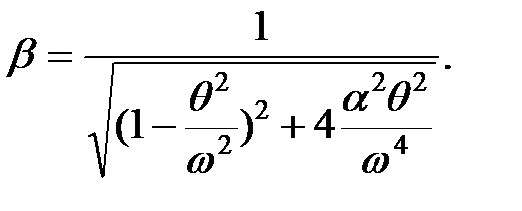
(1.29)

Общее решение уравнения (1.8) находится как сумма общего решения соответствующего однородного уравнения и частного решения неоднородного:

у=у_св+у_част

Общее решение однородного уравнения у_СВ, найденное в предыдущем разделе, представляет собственные колебания, которые с течением времени затухают. Следовательно, у_ЧАСТ представляет незатухающую часть колебаний. Коэффициент 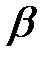показывает, во сколько раз возрастает перемещение при динамическом действии нагрузки по сравнению со статическим ее действием. График 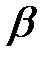показан на рис.1.9. Как видно из этого графика, амплитуды колебаний резко возрастают при 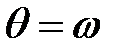. Это явление называется резонансом, а само совпадение частот – условием резонанса.

При 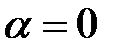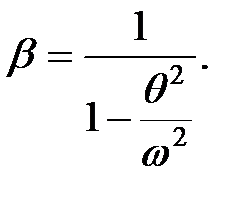Этим значением амплитудного динамического коэффициента можно пользоваться в практических расчетах. Погрешность расчета в данном случае идет в запас прочности.