Свободные колебания без учета сил сопротивления
Уравнения (3.1) без учета сил сопротивления и при отсутствии внешних сил принимают вид
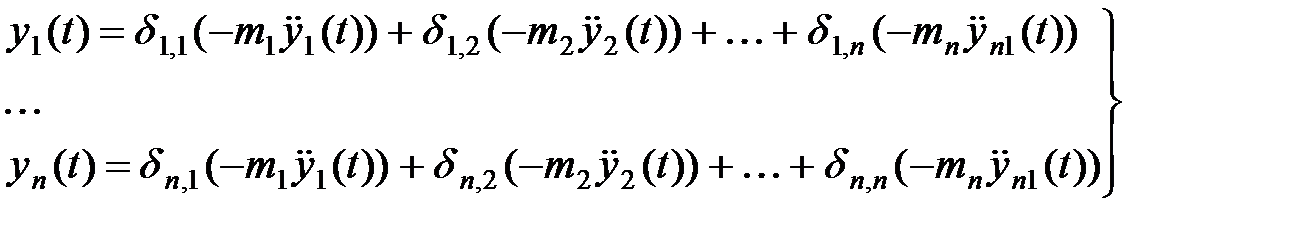
| (3.2) |
Исследования показали, что при свободных колебаниях систем со многими степенями свободы каждая масса движется по гармоническому закону, т.е. закон перемещения i-й массы имеет вид:
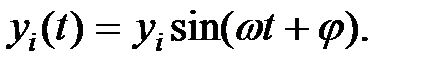
| (3.3) |
Подставляя функции перемещений всех масс и их производные в уравнения (3.2), после приведения подобных членов и сокращения на 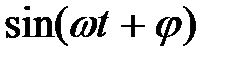 , приходим к следующей системе уравнений:
, приходим к следующей системе уравнений:
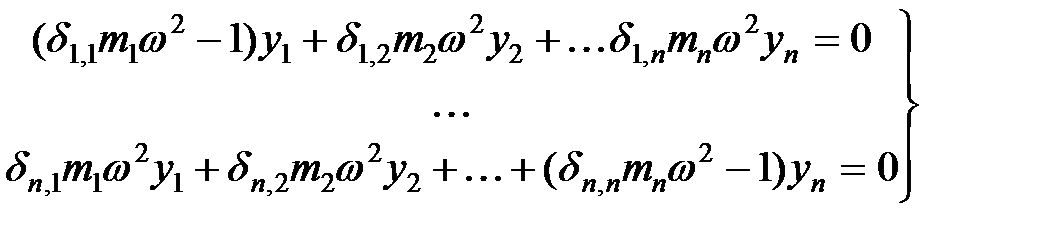 . .
| (3.4) |
Система уравнений (3.4) однородна и вследствие этого имеет два решения. Одно из них – нулевое. Однако в данном случае нулевое решение нас не устраивает, так как это означает отсутствие колебаний. Ненулевое решение имеет место только в том случае, когда определитель, составленный из коэффициентов при неизвестных, равен нулю. Следовательно
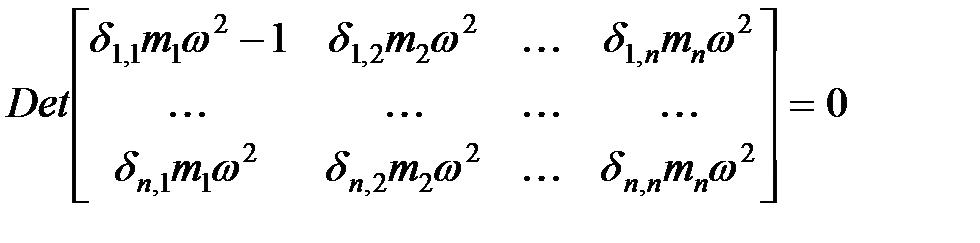 . .
| (3.5) |
Раскрыв определитель (3.5), получим алгебраическое уравнение n-й степени относительно 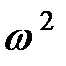 , из которого можно найти n частот собственных колебаний.
, из которого можно найти n частот собственных колебаний.
Каждой частоте собственных колебаний конструкции соответствует своя форма перемещений ее точек, называемая формой собственных колебаний. Найти формы собственных колебаний непосредственно из уравнений (3.4) нельзя, так как матрица этой системы вырождена. Однако для каждой частоты собственных колебаний соответствующая ей форма может быть найдена следующим образом.
Одно из перемещений, например, 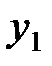 , принимается равным 1. Это значение подставляется во все уравнения. Число неизвестных при этом сокращается на единицу. Первое уравнение отбрасывается, и из оставшихся
, принимается равным 1. Это значение подставляется во все уравнения. Число неизвестных при этом сокращается на единицу. Первое уравнение отбрасывается, и из оставшихся 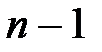 уравнений находятся перемещения
уравнений находятся перемещения 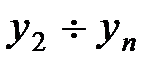 .
.
Дата добавления: 2018-03-01; просмотров: 587;
