Системы с одной степенью свободы. Свободные и вынужденные колебания

Рассмотрим конструкцию с одной сосредоточенной массой, способной перемещаться только в одном направлении (рис.1.1). Такие конструкции называются системами с одной степенью свободы.

Получим уравнение движения этой конструкции статическим способом. При этом учтем, что на массу при ее колебаниях действуют сила сопротивления среды 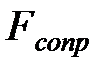и сила инерции 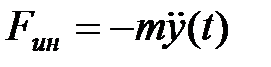.Силу сопротивления принято считать пропорциональной скорости, т.е. 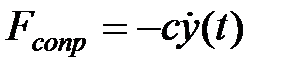.Перемещение массы можно найти следующим способом.

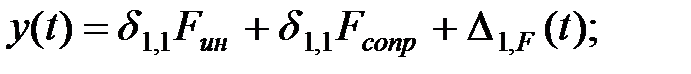
(1.1)

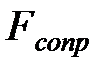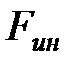После подстановки значений и получаем:

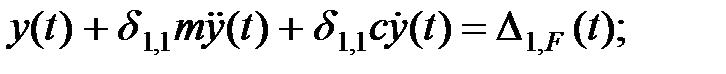
(1.2)

Разделим левую и правую части уравнения (1.2) на 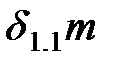и обозначим:

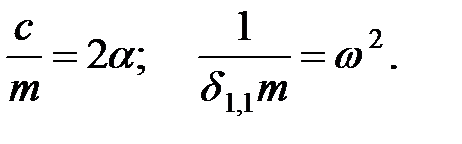
(1.3)

Уравнение (1.2) примет вид:

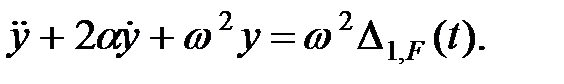
(1.4)

Это и есть уравнение движения системы с одной степенью свободы.

Рассмотрим еще один способ составления уравнения движения. Применим метод перемещений. Наложим связь, как показано на рис.1.2.

Вырежем узел с приложенной к нему массой:

Сумму поперечных сил в балке обозначим 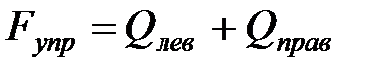и назовем силой упругого сопротивления. Ее можно представить в ви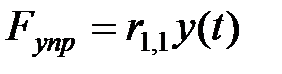де , где 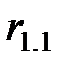- сила упругого сопротивления при единичном перемещении массы. Силу, с которой внешняя нагрузка действует на массу, обозначим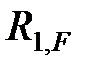

Уравнение равновесия массы имеет вид:

.

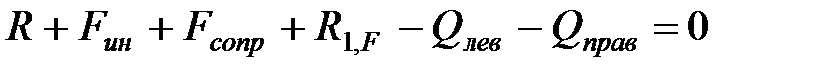(1.5)

Отсюда получаем

.

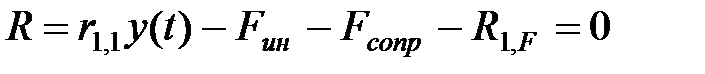(1.6)

Коэффициент 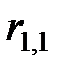в формуле (1.6) представляет реакцию балки на единичное перемещение и называется жесткостью. Иными словами, жесткость равна силе, которую нужно приложить, чтобы сообщить балке единичное перемещение (см. рис.1.4,а). Напомним, что перемещение, вызванное единичной силой, называется податливостью (см.рис.1.4,б).

Применим к двум состояниям конструкции, показанным на рис.1.4, теорему о взаимности работ:

.

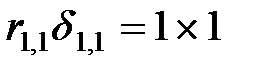Следовательно,

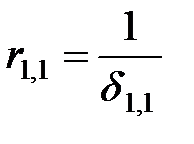
(1.7)

Реакцию в наложенной связи от внешней силы найдем на основании следующих рассуждений.

Перемещение массы от внешней силы равно 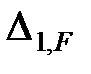. Но если единичное перемещение вызывает реакцию 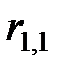, то заданное перемещение вызовет реакцию в 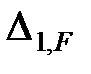раз большую. Таким образом, .

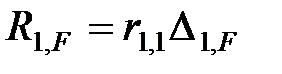Подставляя найденные значения сил в уравнение (1.6), получаем

.

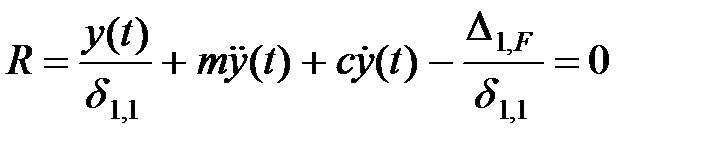(1.8)

Нетрудно убедиться, что при использовании обозначений (1.3) уравнение (1.8) приводится к виду (1.4).