Степень свободы конструкции

Элементы различных конструкций часто подвергаются действию динамических нагрузок. Динамическими называются такие нагрузки, которые, изменяясь во времени, вызывают появление в конструкции инерционных сил. Инерционные силы, в свою очередь, изменяют распределение внутренних усилий в конструкции, причем последние также меняются во времени. Поэтому расчет конструкций на прочность и жесткость при действии динамических нагрузок имеет свою специфику. Сам ход динамического расчета во многом зависит от распределения масс в системе. В связи с этим введем понятие степени свободы конструкции. При выполнении динамических расчетов под степенью свободы конструкции подразумевают число геометрических параметров, определяющих положение масс системы. В принципе любая конструкция представляет собой систему с распределенной массой, или систему с бесконечно большим числом бесконечно малых масс. Таким образом, степень свободы реальной конструкции всегда равна бесконечности. Однако в инженерных расчетах используют расчетные схемы с конечным числом масс. Это возможно в тех случаях, когда на конструкции установлено некоторое оборудование, масса которого намного больше массы самой конструкции, так что последней в расчетах можно пренебречь, и когда в расчетах можно пойти на некоторое уменьшение точности при упрощении расчетной схемы. Примеры такого упрощения будут рассмотрены ниже.

Изменение параметров напряженно-деформированного состояния конструкции во времени под действием динамических нагрузок принято называть вынужденными колебаниями. Однако колебания конструкции возможны и после устранения нагрузок. Такие колебания называются свободными или собственными.

Независимо от вида исследуемых колебаний, методы динамического расчета можно разделить на две категории: статические и энергетические.

Суть статических методов расчета заключается в том, что для каждого момента времени составляются уравнения равновесия, в которых наряду с приложенными внешними силами и возникающими в конструкции внутренними усилиями учитываются еще и инерционные силы. Уравнения равновесия имеют при этом вид:

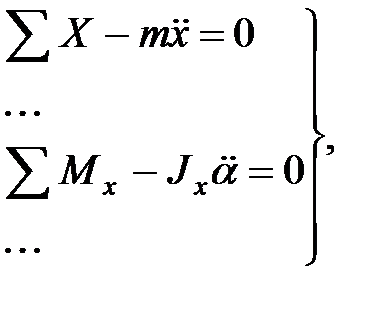
где m –масса, J_X - момент инерции массы, 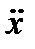- линейное ускорение массы, 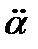- угловое ускорение массы.

Энергетические методы основаны на использовании закона сохранения энергии. Для любой конструкции можно записать закон сохранения энергии в виде:

K+V=const,

где К – кинетическая, а V – потенциальная энергия системы. И та, и другая могут быть выражены с помощью известных соотношений теоретической и строительной механики, а после подстановки их в уравнение закона сохранения энергии из последнего могут быть найдены интересующие расчетчика величины.